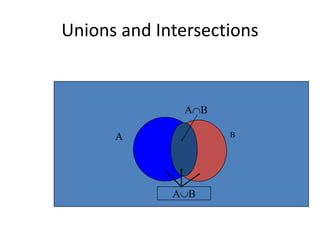
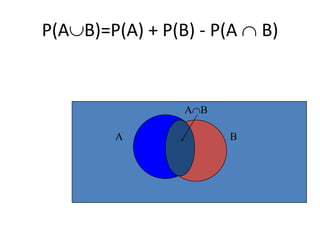
The document defines classical probability and key probability concepts. Probability is defined as the number of ways an event can occur divided by the total number of possible outcomes. There are three types of events: independent events where the occurrence of one does not impact the other, dependent events where the occurrence of one affects the other, and mutually exclusive events that have no outcomes in common. The document also outlines laws of probability, including the addition rule for independent events, the multiplication rule for independent events, and the general addition rule.

1. Probability
Jeanine Blumenau

2. Classical method
Experiment (eg. Flip of a coin – outcome of H or T)
• Exact outcome is unknown before conducting
experiment
• All possible outcomes of experiment are known
• Each outcome is equally likely
• Experiment can be repeated under uniform
conditions
Together these conditions produce regularities or
patterns in outcomes

3. Probability defined
 
Number of ways that can occur
Number of possibilities
E
P E 
• The probability ranges between 0 and 1
• If an outcome cannot occur, its
probability is 0
• If an outcome is sure, it has a probability
of 1

4. • Two events are Independent if the occurrence
of 1 has no effect on the occurrence of the
other. (a coin toss 2 times, the first toss has no
effect on the 2nd toss)

5. Probability of Two Independent Events
(can be extended to probability of 3 or more
independent events)
• A & B are independent events then the
probability that both A & B occur is:
• P(A and B) = P(A) * P(B)

6. Probabilities of dependent events
• Two events A and B are dependent events if
the occurrence of one affects the occurrence
of the other.
• The probability that B will occur given that A
has occurred is called the conditional
probability of B given A and is written P(B|A).

7. Probability of Dependent Events
• If A & B are dependant events, then
the probability that both A & B occur
is:
• P(A and B) = P(A) * P(B│A)

8. Comparing Dependent and Independent
Events
• You randomly select two cards from a standard 52-
card deck. What is the probability that the first card
is not a face card (a king, queen, or jack) and the
second card is a face card if
• (a) you replace the first card before selecting the
second, and
• (b) you do not replace the first card?

9. • (A) If you replace the first card before selecting the
second card, then A and B are independent events.
So, the probability is:
• P(A and B) = P(A) * P(B) = 40 * 12 = 30
52 52 169
• ≈ 0.178
• (B) If you do not replace the first card before
selecting the second card, then A and B are
dependent events. So, the probability is:
• P(A and B) = P(A) * P(B|A) = 40*12 = 40
52 51 221
• ≈ .0181

10. Unions and Intersections
A B
A
A

11. Union of two events
• The union of events A and B is the event
containing all the sample points of either A or B,
or both
• The notation for the union is P(AB).
• Read this as “probability of A union B” or the
“probability of A or B.”
• The probability of A or B is the sum of the
probabilities of all the sample points that are in
either A or B, making sure that none are counted
twice.

12. Intersection of two events
• The intersection of events A and B is the event
containing only the sample points belonging
to both A and B
• The notation for the intersection is P(AB).
• Read this as “probability of A intersection B”
or the “probability of A and B.”
• The probability of A and B is the sum of the
probabilities of all the sample points common
to both A and B.

13. Mutually Exclusive Events
• Mutually exclusive events-no outcomes from S
in common
A
B
A = 

14. Laws of Probability
Addition Rule for mutually exclusive events:
4. If A and B are mutually exclusive (disjoint
events), then
P(A  B) = P(A) + P(B)

15. • 5. For two independent events A and B
P(A  B) = P(A) × P(B)

16. Laws of Probability (cont.)
General Addition Rule
6. For any two events A and B
P(A  B) = P(A) + P(B) – P(A  B)

17. Addition law
P(AB) = P(A) + P(B) – P(AB)
The probability that at least one event occurs is
the probability of one event plus the
probability of the other. But to avoid double
counting, the probability of the intersection of
the two events is subtracted.

18. P(AB)=P(A) + P(B) - P(A B)
A B
A

19. Laws of Probability: Summary
• 1. 0  P(A)  1 for any event A
• 2. P() = 0, P(S) = 1
• 4. If A and B are disjoint events, then
P(A  B) = P(A) + P(B)
• 5. If A and B are independent events, then
P(A  B) = P(A) × P(B)
• 6. For any two events A and B,
P(A  B) = P(A) + P(B) – P(A  B)