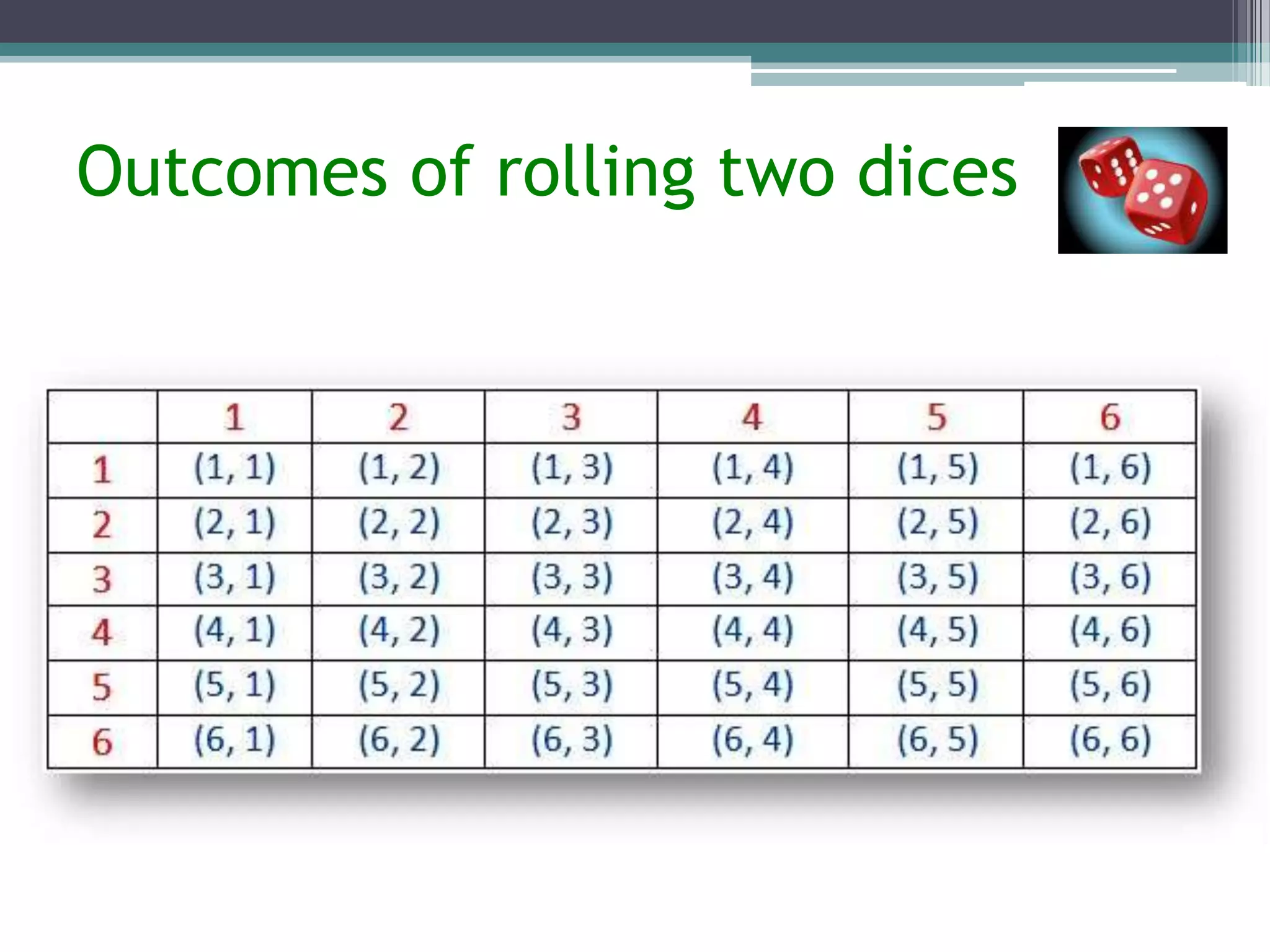
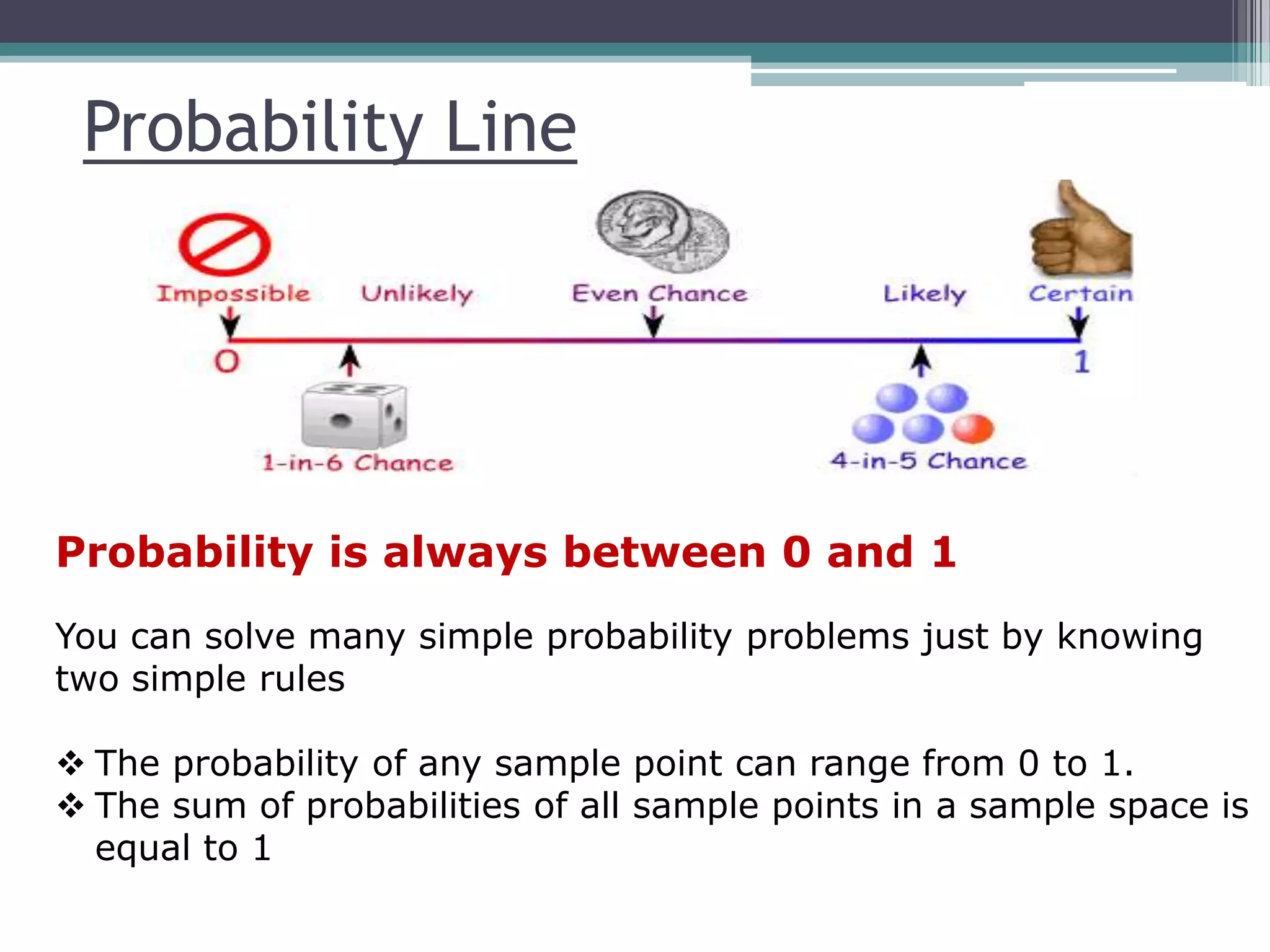
The document discusses probability and statistics. It begins by explaining that the theory of probability was introduced in 1654 by Blaise Pascal and Pierre de Fermat to study gambling problems and formulate the principles of probability. It then discusses key topics in probability like definitions, axioms, conditional probability, total probability, and Bayes' theorem. Examples are provided to illustrate concepts like outcomes of coin tosses, dice rolls, and probability ranges from 0 to 1. Definitions of mutually exclusive, independent, and exhaustive events are explained.

1. PROBABILITY AND STATISTICS

2. 5E Note 4
The theory of probability was introduced by two
famous mathematician Blaise and Pierre de Fermat in
1654. They made a study of the gambling problems
to formulate the fundamental principles of
probability theory. After that it was developed by
Laplace, Chebyshev, Markov, Von Mises and
Kolmogorov.

3. PROBABIILITY
Topics
Definitions of probability
Axioms of probability
Conditional probability
Total probability
Baye’s Theorem

4. Basic Ideas
If a coin is tossed, there are two possible outcomes
heads (H) or tails (T)
Probability of the coin landing H is ½.
And the probability of the coin landing T is ½.
Tossing a Coin

5. Throwing Dice
If a single die is thrown, there are six
possible outcomes:
1, 2, 3, 4, 5, 6.
The probability of any one of them is 1/6.

6. Outcomes of rolling two dices

7. Probability Line
Probability is always between 0 and 1
You can solve many simple probability problems just by knowing
two simple rules
 The probability of any sample point can range from 0 to 1.
 The sum of probabilities of all sample points in a sample space is
equal to 1

8. Definition of probability
If a trial results in n exhaustive mutually exclusive
and equally likely cases and m of them are
favorable to the happening of an event A, than the
probability of happening of A is given by
n
m
S
n
A
n
cases
of
number
Exhaustive
cases
favourable
of
Number
p
A
P 



)
(
)
(
)
(

9. Axioms of probability
Let S be the sample space and A be an event associated
with a random experiment. Then the probability of
the event A, denoted by P(A), is defined as a real
number satisfying the following axioms.
1.
2.
3. If is a complementary event of A then
4. If A and B are mutually exclusive events then
1
)
(
0 
 A
P
0
)
(
,
1
)
( 
 
P
S
P
)
(
1
)
( A
P
A
P 

)
(
)
(
)
( B
P
A
P
AUB
P 

A

10. Mutually Exclusive
• Two sets A and B said to be disjoint or mutually
exclusive if they have no elements in common
ie
Mutually Exclusive Event
Two events A and B are said to be mutually
exclusive if both the event cannot occurs
simultaneously in a single trial.
Example ,in tossing of a coin ,both head and tail
cannot occur in a single trial.


 B
A

11. Independent Event
• Two events A and B are said to be Independent
event if the occurrence of the one event will not
affect the occurrence of the other event.ie ,both
the events can occur simultaneously
Example, in successive tossing of a coin ,the
event of getting a head or tail in the first toss does
not affect the event of getting a head or tail in the
second toss.

12. Example 1
Toss a fair coin twice. What is the
probability of observing at least one head?
H
1st Coin 2nd Coin Ei
P(Ei)
H
T
T
H
T
HH
HT
TH
TT
1/4
1/4
1/4
1/4
P(at least 1 head)
= P(E1) + P(E2) +
P(E3)
= 1/4 + 1/4 +
1/4 = 3/4

13. Example 2
A bowl contains three balls, one red, one
blue and one green. A child selects two
balls at random. What is the probability
that at least one is red?
1st time 2nd time Ei
P(Ei) RB
RG
BR
BG
1/6
1/6
1/6
1/6
1/6
1/6
P(at least 1 red)
= P(RB) + P(BR)+
P(RG) + P(GR)
= 4/6 = 2/3
m
m
m
m
m
m
m
m
m
GB
GR

14. Problems
1. From a pack of 52 cards 1 card is drawn at random.
Find the probability of getting a King.
Solution :
Out of 52 cards 1 card is drawn at random then
Let A be the event of getting a King.
52
52
)
( 1

 ways
C
S
n
4
4
)
( 1

 ways
C
A
n

15. Probability of getting a King
2. A coin is tossed thrice. What is the chance of getting
all heads?
Solution
Let the sample space be
13
1
52
4
)
(
)
(
)
( 


S
n
A
n
A
P
 
8
)
(
,
,
,
,
,
,
,


S
n
TTT
HTT
TTH
THT
THH
THH
HTH
HHH
S

16. Let A be the event of getting all heads.
Probability of getting all heads
 
1
)
( 

A
n
HHH
A
8
1
)
(
)
(
)
( 

S
n
A
n
A
P

17. 3. What is the chance of getting two sixes in two
rolling of a single die
Solution
Let the sample space be
36
)
(
)
6
,
6
.......(
).........
2
,
6
(
),
1
,
6
(
)
6
,
5
........(
).........
2
,
5
(
)
1
,
5
(
)
6
,
4
........(
).........
2
,
4
(
)
1
,
4
(
)
6
,
3
.....(
..........
)
2
,
3
(
)
1
,
3
(
)
6
,
2
........(
).........
2
,
2
(
),
1
,
2
(
)
6
,
1
........(
).........
2
,
1
(
),
1
,
1
(




















S
n
S

18. Let A be the event of getting two sixes in two
rolling of a single die.
Probability of getting two sixes in two rolling of a
single die
 
1
)
(
)
6
,
6
(


A
n
A
36
1
)
(
)
(
)
( 

S
n
A
n
A
P

19. 4. What is the chance that a leap year selected at
random will contain 53 Sundays?
Solution
Let A be the event that there are 53 Sundays in a leap
year. In a leap year (which consists of 366 days), there
are 52 complete weeks and 2 days over. The possible
combinations for these two days are
i) Sunday and Monday
ii) Monday and Tuesday
iii) Tuesday and Wednesday

20. iv) Wednesday and Thursday
v) Thursday and Friday
vi) Friday and Saturday
vii) Saturday and Sunday
The required probability is
7
2
)
( 

cases
of
number
Exhaustive
cases
favourable
of
Number
A
P
)}
,
(
),
,
(
),
,
(
),
,
(
),
,
(
),
,
(
),
,
{(
Sun
Sat
Sat
Fri
Fri
Thus
Thus
Wed
Wed
Tues
Tues
Mon
Mon
Sun
S 
)}
,
(
),
,
{( Sun
Sat
Mon
Sun
A 