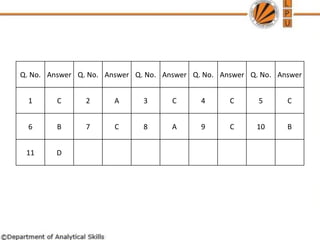
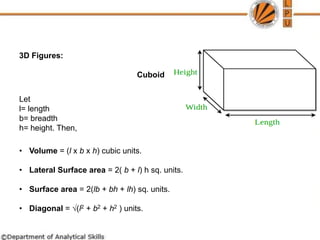
The document provides information about mensuration and clocks:
Mensuration deals with geometric shapes, their areas, volumes, and parameters. It discusses calculating areas and volumes of 2D and 3D shapes like rectangles, squares, triangles, circles, cubes, cylinders, and spheres. Practice questions with solutions are provided to help understand these concepts.
Clocks are also discussed. The key parts of a clock include the dial, hour and minute hands. Formulas are given to calculate the angle between the hands based on the time. Practice questions on clocks focus on reading times from analog clocks and calculating angles between the hands.