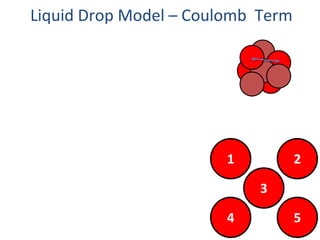
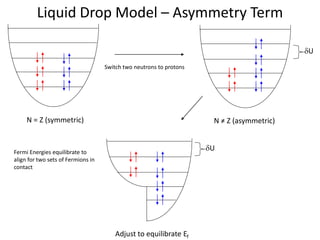
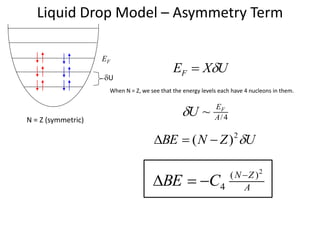
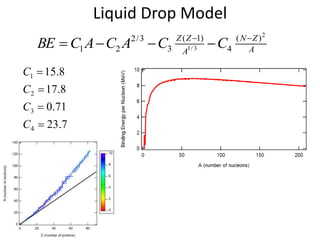
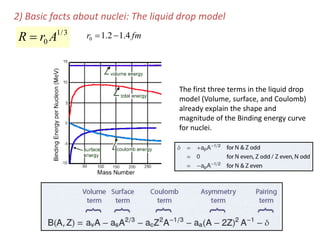
The liquid drop model treats the nucleus like a liquid drop with several terms that contribute to the binding energy. The volume term considers that binding energy increases with the number of nucleons. The surface term accounts for the fact that surface nucleons interact with fewer nucleons. The Coulomb term includes the repulsive force between protons. The asymmetry term makes nuclei with equal numbers of protons and neutrons most stable. Together these terms can explain the general shape of the binding energy curve for nuclei.

1. Liquid Drop Model – Volume Term
The liquid drop model is named from the fact that water sticks to itself, but repels
itself if pushed too close together (incompressible)
We can consider each new nucleon as having the ability to add one new unit of bond
energy to the volume of nucleons. We know the volume increases linearly with A. For
larger volume nuclei, there should be proportionally more binding energy.
New bond
...
1 
 A
c
BE
Consider analogy with liquid drop:
- Liquids often considered as non-compressible
- Density constant, independent of radius
Then: radius R ~ n1/3 where n is number of
molecules/nucleons in drop

2. Liquid Drop Model – Surface Term
The liquid drop model is named from the fact that water sticks to itself, but repels
itself if pushed too close together (incompressible)
The surface nucleons interact with fewer nucleons because they are separated from the
deeper, buried nucleons.
This one can be
pulled off easer
than this one.
3
/
2
2
3
3
/
1
3
3
/
1
3
4
)
(
4
)
(
A
c
BE
R
A
SA
R
A
V
o
o








3. 3
/
1
3 )
1
(
A
Z
Z
c
BE




Liquid Drop Model – Coulomb Term
The liquid drop model is named from the fact that water sticks to itself, but repels
itself if pushed too close together (incompressible)
The protons are pushing against each other. The Coulomb force is much lower than the
strong force, but it still exists to weaken the binding.
R
q
k
R
U
2
)
( 
Some protons are very close and
some are 2R apart. On average,
they are A1/3Ro apart.
o
o
R
A
q
k
R
A
U 3
/
1
2
3
/
1
)
( 
Each proton feels Z - 1 protons
pushing on it. Adding this up for
all Z protons.

4. Liquid Drop Model – Coulomb Term
1 2
3
4 5

5. Liquid Drop Model – Asymmetry Term
Pauli Exclusion makes N = Z the lowest energy. N
= Z allows filling of states in such at way that Pauli
Exclusion can be avoided.
N = Z (symmetric)
EF

6. Liquid Drop Model – Asymmetry Term
Switch two neutrons to protons
dU
N = Z (symmetric) N ≠ Z (asymmetric)
dU
Adjust to equilibrate Ef
Fermi Energies equilibrate to
align for two sets of Fermions in
contact

7. Liquid Drop Model – Asymmetry Term
dBE α j dU
4j dU
U
j
U
j
BE d
d 2
4 


j = number of nucleons being
exchanged
dU
U
Z
N
BE d
2
)
( 


j
Z
N 2


Start with N = Z. Take away two from N. Add two
to Z

8. Liquid Drop Model – Asymmetry Term
N = Z (symmetric)
U
X
EF d

When N = Z, we see that the energy levels each have 4 nucleons in them.
EF
4
/
~ A
EF
U
d
A
Z
N
C
BE
2
)
(
4




dU
U
Z
N
BE d
2
)
( 



9. Liquid Drop Model
A
Z
N
A
Z
Z
C
C
A
C
A
C
BE
2
3
/
1
)
(
4
)
1
(
3
3
/
2
2
1






7
.
23
71
.
0
8
.
17
8
.
15
4
3
2
1




C
C
C
C

10. 2) Basic facts about nuclei: The liquid drop model
3
/
1
0 A
r
R  fm
r 4
.
1
2
.
1
0 

The first three terms in the liquid drop
model (Volume, surface, and Coulomb)
already explain the shape and
magnitude of the Binding energy curve
for nuclei.

11. 11
Typical exam questions:
1) Calculate the binding energy of uranium
238
92 U
2) What percentage is the binding energy of the total nuclear mass?
A = 238
Z = 92
N = 238 - 92 = 146
Binding energy terms (in MeV):
Volume: avA = 15.56 x 238 = 3703.28
Surface: asA2/3 = 17.23 x (238)2/3 = 661.71
Coulomb: acZ2A-1/3 = 0.697 x (92)2 x (238)-1/3 = 951.95
Asymmetry: aa(A-2Z)2A-1 = 23.285 x (238 -184)2 x 238-1 = 285.29
Pairing: apA-1/2 = 12.0 x (238)-1/2 = 0.78
B = +Volume - Surface - Coulomb - Asymmetry + Pairing (N, Z even)
= 3703.28 - 661.71 - 951.95 - 285.29 + 0.78
= 1805.10 MeV
 correct to 0.19%
Masses of unbound nucleons: p = 938.27 MeV/c2, n = 939.57 MeV/c2
Protons: 92 x 938.27 = 86 320.84 MeV/c2
Neutrons: 146 x 939.57 = 137 177.22 MeV/c2
Total: = 223 498.06 MeV/c2
Mass of bound nucleus:
= Mass of unbound nucleons - Binding energy = 223 498.06 - 1805.10 = 221 692.96 MeV/c2
 BE is < 1% of total mass energy of nucleus

12. 12
13.5: Fission Reactors
• Several components are important
for a controlled nuclear reactor:
1) Fissionable fuel
2) Moderator to slow down neutrons
3) Control rods for safety and to control
criticality of reactor
4) Reflector to surround moderator and
fuel in order to contain neutrons
and thereby improve efficiency
5) Reactor vessel and radiation shield
6) Energy transfer systems if commercial
power is desired
• Two main effects can “poison”
reactors: (1) neutrons may be
absorbed without producing fission
[for example, by neutron radiative
capture], and (2) neutrons may
escape from the fuel zone.