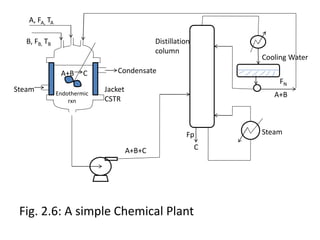
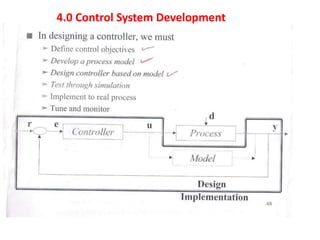
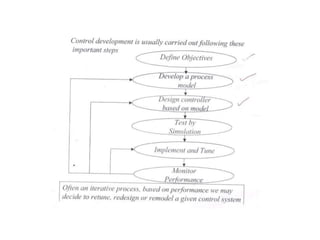
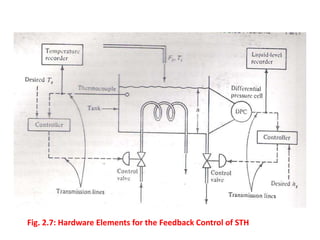
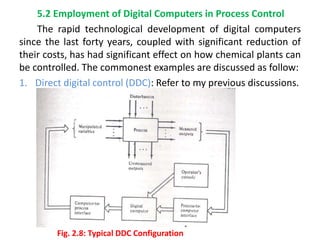
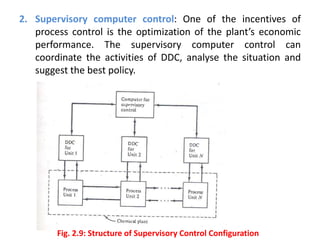
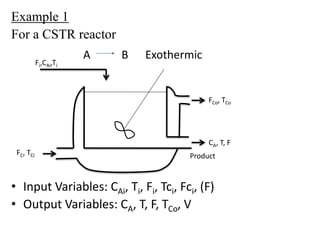
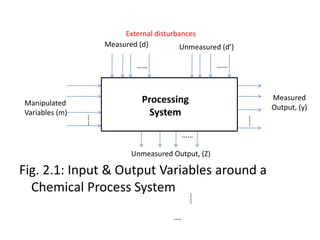
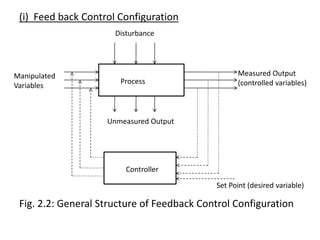
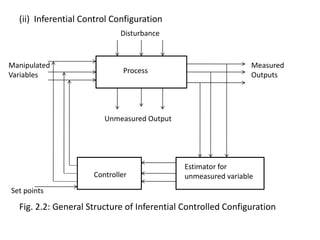
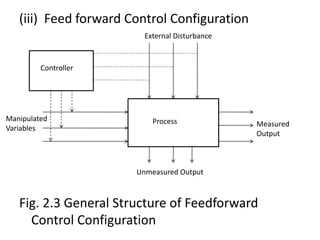
The document provides an overview of process dynamics and control, focusing on the design and hardware aspects of control systems in chemical processes. It discusses the classification of variables, design elements for control objectives, the selection of measurement and control configurations, and the development of controllers. Key hardware elements involved in process control, including sensors, transducers, controllers, and the impact of digital computers, are also highlighted.

1. CHEN502
PROCESS DYNAMICS AND CONTROL
Module 2:
Design and Hardware Aspects of Process
Control System
Prof. Momoh Omuya Raheem
Room 55, PTDF Building
Email: omuyar2002@yahoo.com

2. Learning Outcome
It is the intent of this Module to help the student to:
1. Classify the variables in chemical processes.
2. Identify the design elements of a control system.
3. Develop control aspects of a complete chemical
plant.
4. Highlight control system development.
5. Discuss hardware for a process control system.
2

3. 1. CLASSIFICATION OF THE VARIABLES IN
A CHEMICAL PROCESS
• Input variables denote the effect of
surrounding on the chemical process.
• Output variables denote the effect of the
process on the surrounding.

4. Example 1
For a CSTR reactor
• Input Variables: CAi, Ti, Fi, Tci, Fci, (F)
• Output Variables: CA, T, F, TCo, V
FC, TCi
CA, T, F
FCo, TCo
Product
Fi,CAi,Ti
A B Exothermic

5. Example 2
• For the tank heater
• Input Variables: Fi, Ti, Fst, (F)
• Output Variables: F, V, T
F, T
Fi, Ti
Q
T
h
Steam
Condensate

6. The input variables can be further classified into the
following categories:
a) Manipulated (or Adjustable) variables especially
if their values can be adjusted by an operator or
control mechanism.
b) Disturbance if their values are not resultant
effect of an operator or a control mechanism.
The output variables similarly can be further
divided into the followings:
a) Measured output variables especially if their
values are known by directly measuring them.
b) Unmeasured output variables if they are not or
cannot be measured directly.

7. Fig. 2.1: Input & Output Variables around a
Chemical Process System
External disturbances
Processing
System
Unmeasured Output, (Z)
Measured
Output, (y)
Manipulated
Variables (m)
Measured (d) Unmeasured (d’)
….
…… ……
……
……
……
……

8. 2. DESIGN ELEMENTS OF A CONTROL SYSTEM
(A) Define Control Objectives
Question 1
What are the operational objectives that a
control system is called upon to achieve?
1. Ensuring the stability of a system,
2. Suppressing the influence of external
disturbance,
3. Optimizing the economic performance of a
plant,
4. A combination of the above.
At the beginning the control objectives are
defined qualitatively, subsequently, they are
quantified in terms of the output variables.

9. 1. For CSTR discussed in Example 1, the control objective
(qualitatively defined) is to ensure the stability of unstable
steady state. A quantitative control objective requires that
the temperature (an output variable) not deviate more than
5% from its nominal value at the unstable steady state.
2. For the stirred tank heater (suppressing external
disturbances)
Qualitatively: T and V(h) should be desired value
Quantitatively;
T = Ts
V = Vs Where Ts and Vs are given and they are desired values
3. For the Batch reactor (optimizing the economic performance)
Qualitatively: maximizing profit

10. Quantitatively;
It requires the solution of maximization of profit
which yield the value of the steam flow rate, Q(t);
at each instant during the reaction period.
(B) Select Measurement
Whatever our control objective is, we need some
means to monitor the performance of the chemical
process. This is done by measuring the values of
some certain process variables (Temperature,
Pressure, Flow rate etc).
Question 2
What variables should we measure in order to
monitor the operational performance of the plant?

11. Answer: primary measurements are easy but a secondary
measurement gives mathematical relationship between
unmeasured outputs.
For the Stirred Tank
Simple measurement
T = Ts and V = Vs
Difficult Measurements
A mathematical expression relating the two
Unmeasured Output = f(secondary measurements)
Example
Consider a simple distillation column in the distillate
composition is set 95% pentane against 5% hexane.
Feedback control using analysis
Feedforward control using analysis
Therefore, use a secondary measurement (T)
Analyzer can be
unreliable or very
costly

12. (C) Select the Control Configuration
Question 3
What is the best control configuration for a
given chemical process situation?

13. (i) Feed back Control Configuration
Fig. 2.2: General Structure of Feedback Control Configuration
Process
Controller
Disturbance
Unmeasured Output
Set Point (desired variable)
Measured Output
(controlled variables)
Manipulated
Variables

14. (ii) Inferential Control Configuration
Fig. 2.2: General Structure of Inferential Controlled Configuration
Process
Disturbance
Unmeasured Output
Controller
Estimator for
unmeasured variable
Set points
Measured
Outputs
Manipulated
Variables

15. (iii) Feed forward Control Configuration
Fig. 2.3 General Structure of Feedforward
Control Configuration
Process Measured
Output
Unmeasured Output
Controller
Manipulated
Variables
External Disturbance

16. (D) Design the Controller
In every control configuration the controller is the
active element that receives the information from the
measurements and takes appropriate control action(s) to
adjust the values of the manipulated variables. For the
design of a controller one must answer the next question.
Question 4
How is the information taken from the measurements
used to adjust the values of the manipulated variables?
Answer
Use the control law.
E.g. For the Stirred tank heater
At steady state,
The energy balance of the heater
0 = FρCp(Ti,s – Ts) + Qs ------------------------------------------- (1)

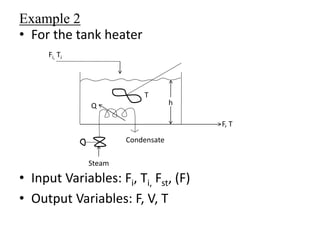
17. Diagrammatically
How T changes with time will be given by the
transient energy balance around the tank; that is
Subtracting eqn 1 from eqn 2, we have
Note that, since Ts = constant
Time
Ts
Ti,s
Ti
dT/dt
=
))/dt
T
-
(d(T s
(3
-
-
-
Qs)
-
(Q
+
Ts)]
-
(T
-
s)
Ti,
-
Cp[(Ti
F
=
Ts))/dt
-
Cp(d(T
V 

(2)
-
-
-
-
Q
+
T)
-
Cp(Ti
F
=
d(T)/dt
Cp
V 


18. The difference, ϵ = T – Ts denotes the error or
deviation of liquid, temperature from the
desired value Ti. We want to drive this error to
zero by manipulating appropriately the value of
heat input, Q. The simplest control law is to
require that Q changes proportionally to the
error T – Ts, hence
Q = -α(T – Ts) + Qs ---------------------- (4)
This law is known as proportional control and
parameter α is called proportional gain.
Substituting eqn4 into eqn3, we have

19. VρCp d(T – Ts)/dt = FρCp[(Ti – Ti,s) – (T – Ts)] – α(T – Ts) -------- (5)
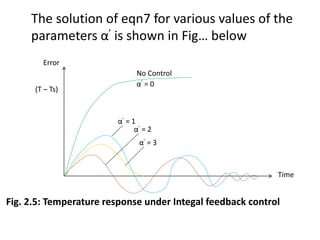
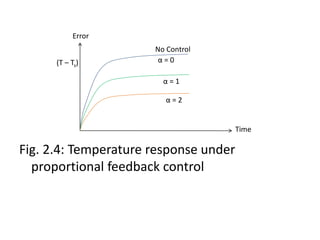
Eqn5 is solved for (T – Ts), and for various values
of gain and yield the solutions shown in Fig..
below. It’s noticed that more of the solutions is
satisfactory since T – Ts ≠ 0. Thus one concludes
that the proportional control law is not
acceptable.

20. Fig. 2.4: Temperature response under
proportional feedback control
Error
Time
(T – Ts)
No Control
α = 0
α = 1
α = 2

21. However, considerable improvement in the
quality of the resulting control can be obtained
if one uses a different control law known as
integral control. In this case Q is proportional to
the time integral of (T – Ts); thus,
Substituting again Q from eqn6 into eqn3, we
have
(6)
-
-
-
-
-
-
-
-
-
Qs
+
Ts)dt
-
(T
'
t
0


 
Q
)
7
(
Ts)dt
-
(T
'
-
]
Ts)
-
(T
-
s)
Ti,
-
Cp[(Ti
F
=
Ts))/dt
-
(d(T
Cp
V
t
0









22. The solution of eqn7 for various values of the
parameters α’ is shown in Fig… below
Time
Error
(T – Ts)
α’ = 1
α’ = 2
α’ = 3
α’ = 0
No Control
Fig. 2.5: Temperature response under Integal feedback control

23. From above, we notice that integral control is
acceptable since it drives the error, T – Ts to
zero. However, we also noticed that depending
on the values of α’, the error T – Ts returns to
faster or slower, oscillates for longer or shorter
time, and so on. In other words, the quality of
control depends on the value of α’.
Combining the proportional with the integral
action, we take a new control law known as
proportional integral control. According to this
law, the value of heat input, Q is given by,

24. We shall see this and other types of control
laws, somewhere later. However, it should be
remembered that the selection of appropriate
control law is an important question to be
answered by the chemical engineer control
design.
Qs
Ts)dt
-
(T
'
-
Ts)
-
(T
-
=
Q
t
0





25. 3.0 Control Aspect Of a Complete Chemical Plant
The examples that we have been discussing in the
previous sections were concerned with the control
of single units such as CSTR, a tank heater, and a
batch reactor. It should be emphasized that rarely if
ever a chemical process composed of one unit only.
On the contrary, a chemical process is composed of
a large number of units (reactors, separators, heat
exchangers, tanks, pumps, etc.) which are inter-
connected with each other through the flow of
materials and energy. For such a process the
problem of designing a control system is not simple
but requires experience and good chemical
engineering background. Consider this simple
example.

26. Fig. 2.6: A simple Chemical Plant
Cooling Water
Steam
Steam
Condensate
Jacket
CSTR
Distillation
column
C
Fp
FN
A+B
A+B+C
A+B C
B, FB, TB
A, FA, TA
Endothermic
rxn

27. The operational objectives for this simple plant
are
1.Product Specifications:
a) To keep the flow rate of the desired product
stream FP at the desired level.
b) Keep the required purity of C in the product
stream
2.Operational Constraints:
a) Do not overflow the CSTR.
b) Do not flood the distillation column or let it dry
3.Economic Considerations:
Maximizing the profit = minimizing the cost of
production through operating costs such as cost
of raw materials, utilities etc

28. The disturbance that will affect the foregoing objectives
are:
a) The flow rates, compositions, and temperature of the
streams of the two raw materials.
b) The pressure in the distillation column.
c) The temperature of the coolant used in the condenser
of the distillation column. (For example, if the coolant
is water. It will have a different temperature during
the day than during the night)
At first glance, the problem of designing a control
system even for this simple plant looks very complex.
Indeed it is. The basically new feature for the control
design of such a system is the interaction between the
units (reactor, column).

29. The output of the reactors affects the operation
of the column in a profound manner and the
overhead product of the column influences the
conversion in the CSTR. This tighten interaction
between the two units seriously complicates the
design of the control system for the overall process.
Suppose that we want to control the
composition of the bottoms product by
manipulating the steam in the reboiler of the
column. This control action will affect the
composition of the overhead product (A+B), which
will in turn affect the reaction conversion in the
CSTR.

30. On the other hand, to keep the conversion in
the CSTR constant at the design level, we try to
keep the ratio FA/FB = constant and the
temperature T in the CSTR constant. Any
changes in FA/FB or T will affect the conversion
in the reactor and thus the composition of the
column will affect the purity of the two product
streams.
The control of integrated processes is the
basic objective for a chemical engineer. One to
its complexity, though, we will start by analyzing
the control problems for single Unit and
eventually we will try the integrated processes.

31. 4.0 Control System Development

35. 5.0 Hardware for a Process Control System
5.1 Hardware Elements of a Control System
In every control configuration, we can distinguish the
following hardware system:
1. The chemical process: It may be unit operation equipment,
reactors, mechanical, etc.,
2. The measuring instruments or sensors: Examples are:
thermocouple, venture meters, gas or liquid
chromatographs, etc.
3. Transducers: These are elements that can convert physical
measurements into signals for easy interpretation, e.g.,
pneumatic or electrical signals.
4. Transmission lines: They are either pneumatic but currently
deployment of electric signals.

36. 5. The controller: This is the hardware element that possess the
“intelligence” to receive information from the measuring
devices and decides appropriate action to be taken. It may
employ simple control law, like, “Proportional (P),
Proportional-Integral (PI), Proportional-Integral-Derivative
(PID), Computer, or complex control law like “Artificial
intelligence (AI)”.
6. The final control elements: These are the elements that
implement the decision taken by the controller. Examples
are: relay switches for on-off control, variable speed pumps,
etc.,
7. Recorders: They are normally employed in providing the
visual demonstration of how chemical process behaves in-
situ or at the control room. Currently, the use of computer
console like Visual Display Unit (VDU) has become very
popular in monitoring the performance of chemical
processes.

37. Fig. 2.7: Hardware Elements for the Feedback Control of STH

38. 5.2 Employment of Digital Computers in Process Control
The rapid technological development of digital computers
since the last forty years, coupled with significant reduction of
their costs, has had significant effect on how chemical plants can
be controlled. The commonest examples are discussed as follow:
1. Direct digital control (DDC): Refer to my previous discussions.
Fig. 2.8: Typical DDC Configuration

39. 2. Supervisory computer control: One of the incentives of
process control is the optimization of the plant’s economic
performance. The supervisory computer control can
coordinate the activities of DDC, analyse the situation and
suggest the best policy.
Fig. 2.9: Structure of Supervisory Control Configuration

40. 3. Scheduling computer control: In this case, the computer can
be used to schedule the operation of a plant depending on
the conditions in the market (demand, supply, prices) change
with time by cutting production to avoid overstocking,
increasing production, new production line, etc.

41. ASK YOUR QUESTIONS
IF ANY !!!

42. Thank U all for listening