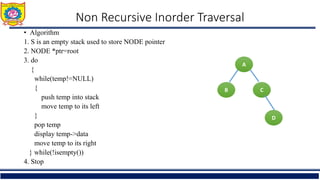
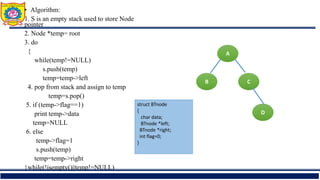
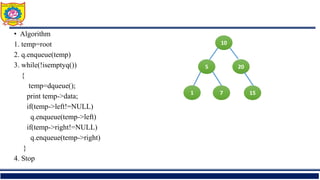
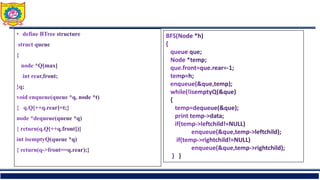
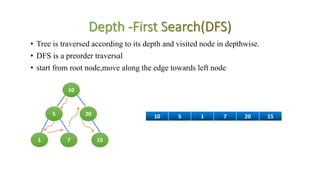
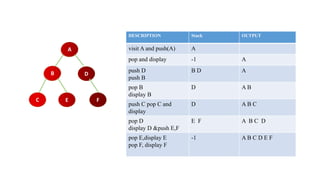
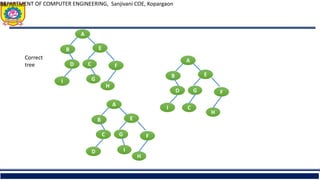
The document outlines the structure and properties of binary trees in computer engineering, detailing definitions, types, and basic operations such as insertion and traversal. It includes examples and algorithms for various types of binary trees, including skewed, complete, and strictly binary trees, along with traversal methods like in-order, pre-order, and post-order. Additional sections cover the construction of binary trees from given traversals and discuss non-recursive traversal techniques.

1. Sanjivani Rural Education Society’s
Sanjivani College of Engineering, Kopargaon-423 603
(An Autonomous Institute, Affiliated to Savitribai Phule Pune University, Pune)
NACC ‘A’ Grade Accredited, ISO 9001:2015 Certified
Department of Computer Engineering
(NBA Accredited)
Prof.B.B.Kotame
Subject- Data Structures-II(CO214)
Unit-I Tree

2. Binary Tree
• In binary tree, every node can have at
most two branches i.e. there is no
node with degree greater than two.
• Definition:
- A binary tree is a finite set of nodes,
which is either empty or consist of a
T and two disjoint binary tree called
as left sub tree and the right sub tree.
DEPARTMENT OF COMPUTER ENGINEERING, Sanjivani COE, Kopargaon 2
A
B C
D F
E G

3. - Difference between tree and binary tree
1. For every node may have left sub tree and right sub tree whereas in tree
sub tree doesn’t matter.
2. Binary tree can have zero nodes i.e. binary tree can be empty, which is
not in case of tree
3.
DEPARTMENT OF COMPUTER ENGINEERING, Sanjivani COE, Kopargaon 3
A
B
A
B
In this example 1st binary tree has empty right sub tree
while second binary tree has empty left tree. if we consider
as tree then both are same only representation is different.

4. DEPARTMENT OF COMPUTER ENGINEERING, Sanjivani COE, Kopargaon 4
1. Minimum number of nodes in a binary tree of height H = H + 1
Example-
To construct a binary tree of height = 4, we need at least 4 + 1 = 5 nodes.
2. Maximum number of nodes in a binary tree of height H= 2H+1 – 1
Example-
Maximum number of nodes in a binary tree of height 3
= 23+1 – 1
= 16 – 1
= 15 nodes
Properties of Binary Tree

5. 3. Total Number of leaf nodes in a Binary Tree
= Total Number of nodes with 2 children + 1
Here, Number of leaf nodes = 3, Number of nodes with 2 children = 2
• Clearly, number of leaf nodes is one greater than number of nodes with
2 children.
DEPARTMENT OF COMPUTER ENGINEERING, Sanjivani COE, Kopargaon 5
4. Maximum number of nodes at any level ‘L’ in a binary tree= 2L
Example-
Maximum number of nodes at level-2 in a binary tree
= 22
= 4
Thus, in a binary tree, maximum number of nodes that can be present
at level-2 = 4.

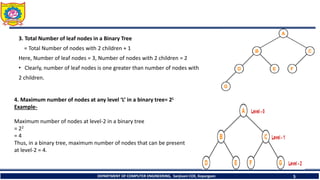
6. 1. The height of a binary tree that contains n, n>=0 element is atmost n and atleast [log2(n+1)]
example: log2(n+1) if n=15
= log2 (15+1)=log(16)/log(2)
= 4 (n<= 2h-1)
DEPARTMENT OF COMPUTER ENGINEERING, Sanjivani COE, Kopargaon 6

7. Exercise
1. A binary tree T has n leaf nodes. The number of nodes of degree-2 in T is ______?
1.Log2n 2.n-1 3.n 4. 2n
2. In a binary tree, the number of internal nodes of degree-1 is 5 and the number of internal nodes of degree-2
is 10. The number of leaf nodes in the binary tree is ______?
1. 10 2.11 3.12 4.15
3. A binary tree T has 20 leaves. The number of nodes in T having 2 children is ______?
1. 20 2.10 3.19 4.15
DEPARTMENT OF COMPUTER ENGINEERING, Sanjivani COE, Kopargaon 7

8. Type of Binary Tree
1. Skewed Binary Tree: a binary tree in which every
node is having either only left sub tree or right sub
tree
2. Almost Complete Binary Tree: In a complete
binary tree, each non-leaf node compulsory has sub
tree. Also, in the last or the lowest level of this
binary tree, every node should possibly reside
on the left side. Here is the structure of a
complete binary tree:
DEPARTMENT OF COMPUTER ENGINEERING, Sanjivani COE, Kopargaon 8
B
C
B
C
A
B C
D F
J
E G
H I

9. DEPARTMENT OF COMPUTER ENGINEERING, Sanjivani COE, Kopargaon 9
Strictly Binary Tree: if every non-terminal node in a binary tree consist of non-
empty left sub tree and right sub tree then such tree is called as strictly binary tree.
- In other words internal node will have either two children or no child at all.
A
B C
D E
F G

10. DEPARTMENT OF COMPUTER ENGINEERING, Sanjivani COE, Kopargaon 10
Complete Binary Tree/Perfect Binary Tree:
• -A complete binary tree is a binary tree
that satisfies the following 2 properties-
• Every internal node has exactly 2 children.
• All the leaf nodes are at the same level.
• Complete binary tree is also called
as Perfect binary tree.

11. • Extended Binary Tree:
- Each empty sub tree is replaced by a failure node. A failure node is represented by
- Any binary tree can be converted into a extended binary tree by replacing each
empty sub tree by a failure nodes
DEPARTMENT OF COMPUTER ENGINEERING, Sanjivani COE, Kopargaon 11

12. Representation of Binary Tree
• To represent the binary tree in one dimensional array, we need to numbered the
nodes sequentially level by level(left to right).
• Every empty nodes are also numbered. e.g.
DEPARTMENT OF COMPUTER ENGINEERING, Sanjivani COE, Kopargaon 12
A
C
B
G
F
E
D
7 A B C D E F G
A
C
B
G
D
G
D
13 A B C - G D - - - - - E F

13. • For complete Binary tree there is no issue, but for skew tree there is a lot of
wastage of space. e.g k depth of skew requires 2k-1 space out of only k get
occupied in array.
• Therefore another way is needed to represent the Binary tree. That is nothing but
linked representation which is an efficient way than array.
DEPARTMENT OF COMPUTER ENGINEERING, Sanjivani COE, Kopargaon 13

14. • The code to write a tree node would be similar to what is given below. It has a data part and references
to its left and right child nodes.
In a tree, all nodes share common construct.
Binary Tree Node

16. Linked representation of Binary Tree

17. Conversion of Tree into Binary Tree
• Children of parents added using leftmost child's right sibling relation.
DEPARTMENT OF COMPUTER ENGINEERING, Sanjivani COE, Kopargaon 17
A
C
B
G
F
E
D
H
I J
K
A
B

18. Examples for Exercise
DEPARTMENT OF COMPUTER ENGINEERING, Sanjivani COE, Kopargaon 18
A
C
D
B
F
E G H I J
A
C
D
B
H
E F
G K
J
I

19. The basic operations that can be performed on a binary tree data structure, are the
following −
Insert − Inserts an element in a tree/create a tree.
Traversals − Searches an element in a tree.
Preorder Traversal − Traverses a tree in a pre-order manner.
Inorder Traversal − Traverses a tree in an in-order manner.
Postorder Traversal − Traverses a tree in a post-order manner.
Search- Search an element in tree using traversals.
Delete- delete an element from binary tree
Binary tree Basic Operations

20. Create/Insert OPERATION
• The very first insertion creates the tree. Afterwards, whenever an element is to be inserted, first locate its
proper location. Start searching from the T node, then search for the empty location in the left subtree and
insert the data. Otherwise, search for the empty location in the right subtree and insert the data.
• Algorithm:
1. Enter key to be inserted. Create node as tempNode for it.
2. Check T is NULL, if yes then make tempNode as T of tree
3. If T is not NULL then
4. Take temporary variable *ptr and set *ptr=T
5. Do
i. Ask user in which direction user wants to insert data(Left or right)
ii. if direction is Left the check following condition

21. iii. if(ptr->left==NULL) //insert node at left of tree
{
ptr->left=tempNode;
break; }
else{
ptr=ptr->left;
}
else //if user gives right direction
{
if(ptr->right==NULL)
{
ptr->right=tempNode;
break;
}
else
{
ptr=ptr->right;
}
}
iv. Do step 5 while(ptr!=NULL)
5. Repeat steps 1 to 5 until no more data to
insert.
6. Stop

22. • Btree.cpp
• Enter the element=4
• Do u want to enter more elements (y/n)y
• Enter the element=12
• in which direction(l/r)l
• Do u want to enter more elements (y/n)y
• Enter the element=34
• in which direction(l/r)l
• in which direction(l/r)?r
• Do u want to enter more elements (y/n)y
• Enter the element=1
• in which direction(l/r)r
• Do u want to enter more elements (y/n)y
• Enter the element=22
• in which direction(l/r)r
• in which direction(l/r)?r
• Do u want to enter more elements (y/n)y
• Enter the element=32
• in which direction(l/r)r
• in which direction(l/r)?l
4
12
34
1
22
32

23. Binary Tree Traversal
• Traversal is a process to visit all the nodes of a tree and print their values too. Because, all nodes are
connected via edges (links) we always start from the T (head) node.
• This process could be defined recursively.
• We cannot access a node randomly from a tree. There are three ways which we use to traverse a tree −
• In-order Traversal
• Pre-order Traversal
• Post-order Traversal

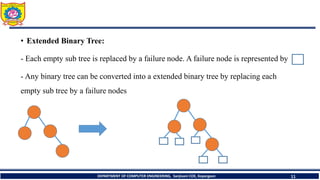
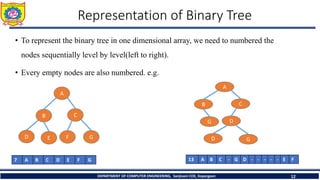
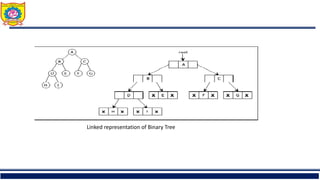
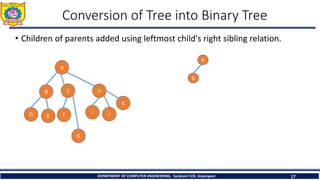
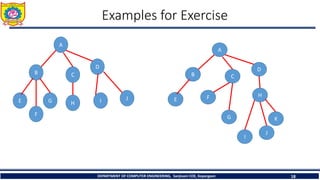
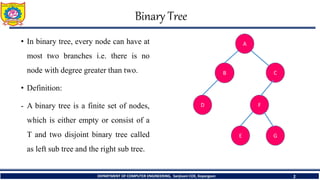
24. 1. In - Order Traversal ( LeftChild - T - RightChild )
Algorithm for inorder traversal
Step 1 : Start from the Left Subtree of T .
Step 2 : Then, visit the T.
Step 3 : Then, go to the Right Subtree.
Step 1 : Inoredr on (B) + A+(Inorder on C)
Step 2 : [B+ inorder on(D) ]+A+ (Inorder on C)
Step 3 : B + inorder on(E) + D + Inorder on( F )+ A +Inorder on (C)
Step 4 : B + E + D + F + A +Inorder on(G)+C+ Inorder on(H)
Step 4 : B + E + D + F + A +G+C+ H
Inorder Traversal : B E D F A G C H

25. 2. Pre - Order Traversal ( T - LeftChild - RightChild )
Step 1 : A + Preorder on (B) + Preorder on(C)
Step 2 : A + [B + Preorder on(D)] +Preorder on (C )
Step 3 : A + [B +[D + Preorder on(E )+Preorder on( F)]] + Preorder on (C )
Step 4: A+ B+ D+ E+ F+ [C+Preorder on(G)+Preorder on(H)]
Step 5: A + B + D+ E+ F + C+ G + H
Preorder Traversal : A B D E F C G H
Algorithm for preorder traversal
Step 1 : Start from the T and visit the T.
Step 2 : Then, go to the Left Subtree.
Step 3 : Then, go to the Right Subtree.

26. • Algorithm for post-order traversal
Step 1 : Start from the Left Subtree (Last Leaf) and visit it.
Step 2 : Then, go to the Right Subtree.
Step 3 : Then, go to the T.
Step 1 : (Postorder on (B) + Postorder on (C) + ( A)
Step 2 : [Postorder on(D)+ B]+ Postorder on (C) + ( A)
Step 2 : [[Postorder on(E)+Postorder on(F)+D]+ B]+ Postorder on (C) + ( A)
Step 3 : E + F + D + B + [[Postorder on(G)+ Postorder on(H)]+C]+A
Step 3 : E + F + D + B + G + H + C + A
Post-order Traversal : E F D B G H C A
3. Post - Order Traversal ( Left-Child – Right-Child - T )

27. void pre_order_traversal(struct node* T)
{
if(T != NULL)
{
cout<<T->data;
pre_order_traversal(T->leftChild);
pre_order_traversal(T->rightChild);
}
}
void inorder_traversal(struct node* T)
{
if(T != NULL)
{
inorder_traversal(T->leftChild);
cout<<T->data;
inorder_traversal(T->rightChild);
}
}
void post_order_traversal(struct node* T)
{
if(T != NULL)
{
post_order_traversal(T->leftChild);
post_order_traversal(T->rightChild);
cout<<T->data;
}
}

28. Construction of Binary Tree from Traversal
Inorder- B I D A C G E H F
Postorder- I D B G C H F E A

29. Construction of Binary Tree from Traversal
Preorder- A B C D E F G H I
Inorder- B C A E D G H F I

30. DEPARTMENT OF COMPUTER ENGINEERING, Sanjivani COE, Kopargaon
30

31. Non-Recursive Preorder
• Algorithm:
1. S is an empty stack used to store NODE pointer
2. NODE *temp
3.push(root)
4. while(stack is not empty)
{
temp=pop();
print temp->data;
if temp has right child then push into stack
if temp has left child then push into stack
}
5.stop

32. Example
A
B C
D
push(root)
temp=pop()
temp=
push(temp->right)
push(temp->left) A
Stack
Operations
A B C D
while(stack is not empty)
{
temp=pop();
print temp->data;
if temp has right child then push into stack
if temp has left child then push into stack
}

33. DEPARTMENT OF COMPUTER ENGINEERING, Sanjivani COE, Kopargaon
33
A
B C
F
D
E

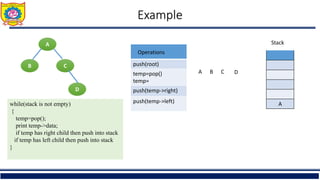
34. struct stack
{
struct node *st[max];
int top;
}s;
s.top=-1;
struct Node
{
struct Node*left;
struct node *right;
int data;
}

35. Non Recursive Inorder Traversal
• Algorithm
1. S is an empty stack used to store NODE pointer
2. NODE *ptr=root
3. do
{
while(temp!=NULL)
{
push temp into stack
move temp to its left
}
pop temp
display temp->data
move temp to its right
} while(!isempty())
4. Stop
A
B C
D

36. DEPARTMENT OF COMPUTER ENGINEERING, Sanjivani COE, Kopargaon
36
A
B C
D

38. • Algorithm
In this traversal each node is visited twice but we are supposed to dispaly
only once.
- Hence there should be some mechanism to indicate whether the node is being
visited 1st time or 2nd time.
- Display the content of the node only when it is visited for the 2nd time.
Non Recursive Postorder Traversal

39. • Algorithm:
1. S is an empty stack used to store Node
pointer
2. Node *temp= root
3. do
{
while(temp!=NULL)
s.push(temp)
temp=temp->left
4. pop from stack and assign to temp
temp=s.pop()
5. if (temp->flag==1)
print temp->data
temp=NULL
6. else
temp->flag=1
s.push(temp)
temp=temp->right
}while(!isempty()||temp!=NULL)
A
B C
D
struct BTnode
{
char data;
BTnode *left;
BTnode *right;
int flag=0;
}

40. DEPARTMENT OF COMPUTER ENGINEERING, Sanjivani COE, Kopargaon
40
A
B C
D

41. • inorder,preorder and postorder requires stack for traversal, but there are some
traversal techniques which requires queue e.g. BFS
• This traversal is also called as Level order traversal as it visits nodes in levels
e.g.
10
5 20
15
1 7
10 5 20 1 7 15

42. • Algorithm
1. temp=root
2. q.enqueue(temp)
3. while(!isemptyq())
{
temp=dqueue();
print temp->data;
if(temp->left!=NULL)
q.enqueue(temp->left)
if(temp->right!=NULL)
q.enqueue(temp->right)
}
4. Stop
10
5 20
15
1 7

43. • BFS is generally used for finding minimum cost edges.
• In peer to peer network, to find all neighbour nodes

45. • Tree is traversed according to its depth and visited node in depthwise.
• DFS is a preorder traversal
• start from root node,move along the edge towards left node
10
5 20
15
1 7
10 5 1 7 20 15

46. • Algorithm
1. Visit the root node. push it into stack
2. Pop the node and display data.
3. if right child is not NULL,push it into stack
4. if left child is not NULL,push it into stack
5. repeat step 2-4 until stack is empty Applications:
1. Topological sorting-> for scheduling jobs
from given dependencies among jobs
2. Path finding: use stack to keep track of
the path between source vertex to
destination vertex

47. 10
5 D
F
A
B
C E
DESCRIPTION Stack OUTPUT
visit A and push(A) A
pop and display -1 A
push D
push B
B D A
pop B
display B
D A B
push C pop C and
display
D A B C
pop D
display D &push E,F
E F A B C D
pop E,display E
pop F, display F
-1 A B C D E F

48. Binary Search Tree
• When we store order data into array structure we use efficient search algorithm.e.g. Binary Search
• However, to provide efficient insertion and deletion operation,we represent a link list.
• The problem with linked list is that their search algo. which are sequential searches,very
ineffecient.
• So what we need is data structure that has efficient search algo. and at the same time efficient
insertion and deletion operation.
• Binary Search Tree provide that structure.

49. Cont...
Defination: A Binary search tree is a binary tree with following properties:
1. All keys are distincts.
2. All items in the right subtree are greater than equal to the root.
3. each subtree is itself a binary search tree.
6
17
19
10
5 20
25
10
8
5 9
22
17
19
10
5 20
12
17
8
11 15

50. BinarySearchTree(BST)
A
s
h
i
m
L
a
m
i
c
h
h
a
n
e
5
0
• A binary search tree (BST) is a binary tree that is either empty or in
which every node contains a key (value) and satisfies the following
conditions:
• All keys in the left sub-tree of the root are smaller than the key in the root
node
• All keysin the right sub-tree of the root are greater than the keyin the root
node
• Theleft and right sub-trees of the root are again binary search trees

51. BinarySearchTree(BST)
A
s
h
i
m
L
a
m
i
c
h
h
a
n
e
5
1
• Abinary search tree is basically abinary tree, and therefore it canbe
traversed in inorder, preorder andpostorder.
• If we traverse abinary search tree in inorder and print the identifiers
contained in the nodes of the tree, we get asorted list of identifiers in
ascending order.

52. BinarySearchTree(BST)
A
s
h
i
m
L
a
m
i
c
h
h
a
n
e
5
2
Time Complexity
Array Linked List BST
Search O(n) O(n) O(logn)
Insert O(1) O(1) O(logn)
Remove O(n) O(n) O(logn)

53. DEPARTMENT OF COMPUTER ENGINEERING, Sanjivani COE, Kopargaon
53
A
B E
F
D
I
C
G
H
A
B E
F
D
I
G
C
H
A
B E
F
C
D
G
I
H
Correct
tree