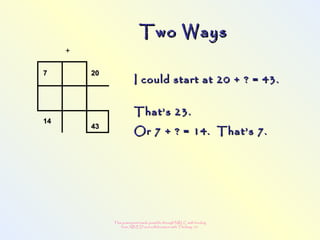
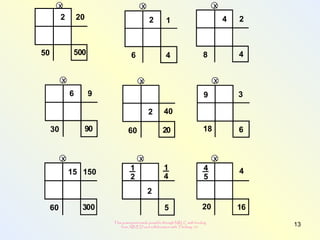
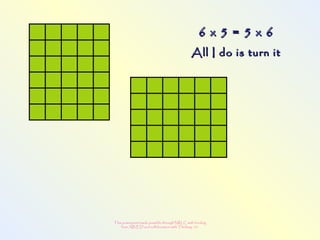
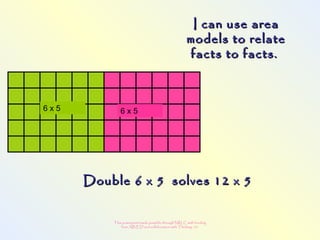
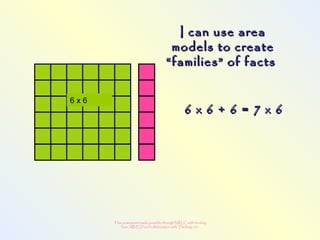
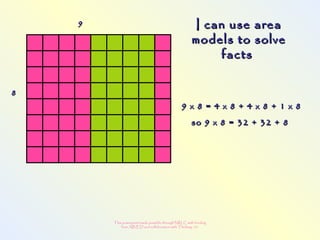
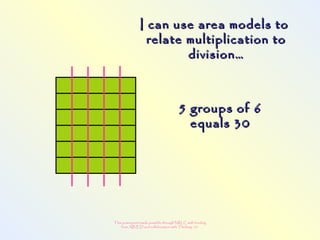
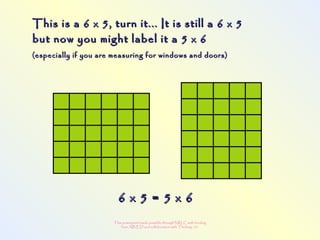
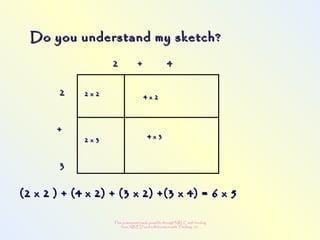
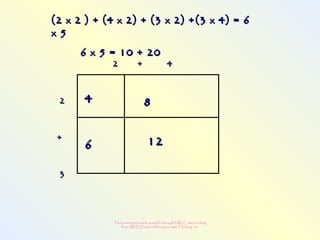
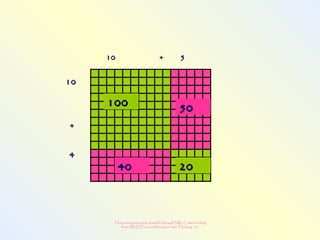
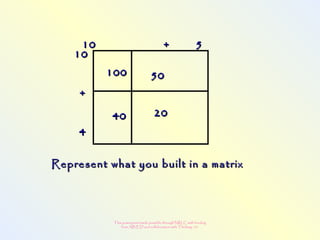
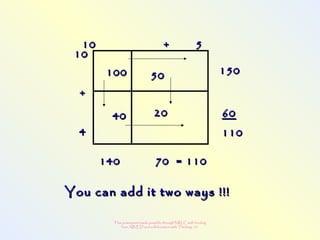
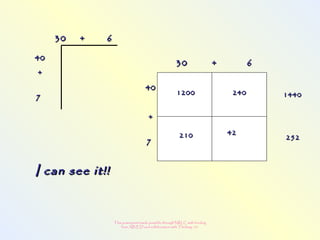
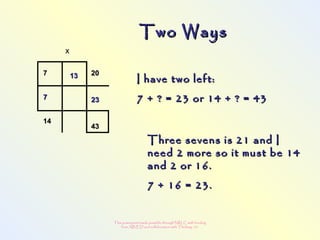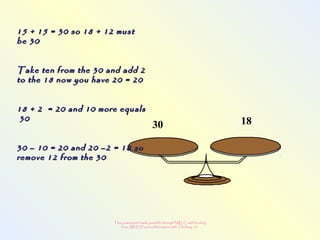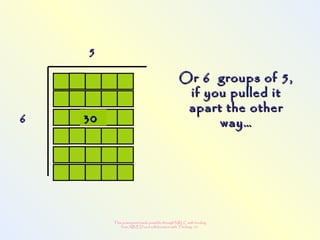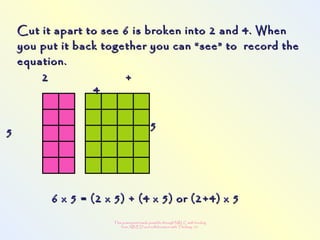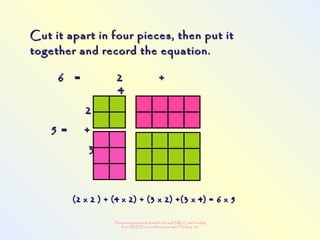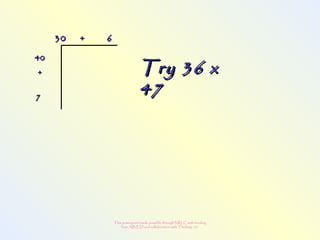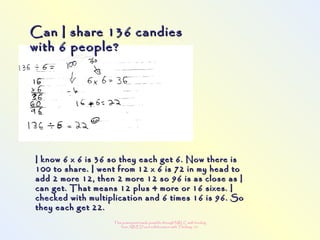The document discusses changes to the mathematics program to better prepare students for the 21st century. It focuses on developing number sense, conceptual understanding, and problem solving skills rather than memorization. Students will learn through activities that build relationships and understanding, like using area models to represent multiplication and see connections between facts. Parents may see different types of learning activities aimed at developing understanding over practicing routines.

1. This powerpoint made possible through NRLC with funding
from AB ED and collaboration with Thinking 101
AGENDAAGENDA
• Why has the mathematics program changed?Why has the mathematics program changed?
• What has changed?What has changed?
• What about the Basics?What about the Basics?
• What Might I See in My Child’s Work?What Might I See in My Child’s Work?
• How Can I Help at Home?How Can I Help at Home?
• Frequently Asked QuestionsFrequently Asked Questions

2. This powerpoint made possible through NRLC with funding
from AB ED and collaboration with Thinking 101
To meet the demands of the 21To meet the demands of the 21stst
Century aCentury a
Balanced mathematics programBalanced mathematics program
Requires students to:Requires students to:
• become proficient with basic skillsbecome proficient with basic skills
• develop conceptual understandingdevelop conceptual understanding
• become adept at problem solvingbecome adept at problem solving

3. This powerpoint made possible through NRLC with funding
from AB ED and collaboration with Thinking 101
Current research on how students learnCurrent research on how students learn
mathematics indicates learning tomathematics indicates learning to think, reasonthink, reason
andand see relationshipssee relationships is the key to long termis the key to long term
success.success.
International evidence indicates that by grade 6International evidence indicates that by grade 6
students are overloaded with trying to rememberstudents are overloaded with trying to remember
rules and formulas.rules and formulas.
Reducing the content allows time for studentsReducing the content allows time for students
to develop understanding.to develop understanding.

4. This powerpoint made possible through NRLC with funding
from AB ED and collaboration with Thinking 101
Number SenseNumber Sense
Fluency and Flexibility;Fluency and Flexibility;
Manipulate numbers confidently andManipulate numbers confidently and
comfortablycomfortably

5. This powerpoint made possible through NRLC with funding
from AB ED and collaboration with Thinking 101
Number Sense develops asNumber Sense develops as
students build, describe, take apartstudents build, describe, take apart
and put together numbersand put together numbers

6. This powerpoint made possible through NRLC with funding
from AB ED and collaboration with Thinking 101
• To promote number sense learning activities moveTo promote number sense learning activities move
from memorizing and drilling to making sense,from memorizing and drilling to making sense,
discussing and explaining how and why numbersdiscussing and explaining how and why numbers
are related.are related.
• Your child may be doing different kinds ofYour child may be doing different kinds of
learning activities than before.learning activities than before.

7. This powerpoint made possible through NRLC with funding
from AB ED and collaboration with Thinking 101
+
Two WaysTwo Ways
77 2020
1414
4343
I could start at 20 + ? = 43.I could start at 20 + ? = 43.
That’s 23.That’s 23.
OrOr 7 + ? = 14. That’s 7.7 + ? = 14. That’s 7.

8. This powerpoint made possible through NRLC with funding
from AB ED and collaboration with Thinking 101
x
Two WaysTwo Ways
77 2020
1414
4343
232377
Now I have 7 + ? = 20Now I have 7 + ? = 20
across the top.across the top.
Three sevens is 21 so itThree sevens is 21 so it
must be one less than twomust be one less than two
sevens. That’s 13sevens. That’s 13

9. This powerpoint made possible through NRLC with funding
from AB ED and collaboration with Thinking 101
x
Two WaysTwo Ways
77 2020
1414
4343
232377
1313
I have two left:I have two left:
7 + ? = 23 or 14 + ? = 437 + ? = 23 or 14 + ? = 43
Three sevens is 21 and IThree sevens is 21 and I
need 2 more so it must be 14need 2 more so it must be 14
and 2 or 16.and 2 or 16.
7 + 16 = 23.7 + 16 = 23.

10. This powerpoint made possible through NRLC with funding
from AB ED and collaboration with Thinking 101
x
Two WaysTwo Ways
77 2020
1414
4343
232377 1616
1313
14 + ? = 43 or 13 + 16 = ?14 + ? = 43 or 13 + 16 = ?
I think I will add down 13 +I think I will add down 13 +
16 = 29.16 = 29.

11. This powerpoint made possible through NRLC with funding
from AB ED and collaboration with Thinking 101
x
Two WaysTwo Ways
77 2020
1414
4343
232377 1616
1313
Twenty nine works for 14 + ? = 43….Twenty nine works for 14 + ? = 43….
because 29 + 14 = 30 + 13because 29 + 14 = 30 + 13
2929

12. This powerpoint made possible through NRLC with funding
from AB ED and collaboration with Thinking 101
Two Ways are an excellent way toTwo Ways are an excellent way to
encourage students to explain theirencourage students to explain their
thinking as they practise “facts”.thinking as they practise “facts”.
Where would you start on the following page?Where would you start on the following page?

13. This powerpoint made possible through NRLC with funding
from AB ED and collaboration with Thinking 101 13
x x x
x
x
9030
5
2
6
16
4
20
x x
500
20
50
2
x
300
150
60
15
x
4
1
6
2
20
40
60
2
4
2
8
4
9 3
18 6
9
4
5
1
4
1
2

14. This powerpoint made possible through NRLC with funding
from AB ED and collaboration with Thinking 101
There are 54There are 54
meaningfulmeaningful
computationscomputations
in one page ofin one page of
Two Ways.Two Ways.
__ x 2 = 20 500 ÷ 20 = __ 50 x __ = 500 50 ÷ 10 = __ 10 ÷ 2 = __
5 + __ = 25 __ x 2 = 1 1 x __ = 4 6 ÷ 1/2 = __ 6 x __ = 4
2 x __ = 3/4 12 x __ = 4 __ x 4 = 2 2 ÷ 16 = __ 8 x __ = 4
1/2 x __ = 8 30 ÷ 1 1/2 9 x __ = 90 30 x __ = 90 6 x __ = 3
20 x __ = 3 20 x __ = 10 20 ÷ 40 = __ 60 x __ = 20 1/2 ÷ 3 = __
20 ÷ 40 = 1/2 3 x __ = 1/2 40 ÷ 2 = __ 3 x __ = 60 1/6 x 2 = __
32 x __ = 4 1/4 ÷1/2 = __ 16 x __ = 1 16 ÷ 32 = __ 1/8 x 1/2 = __
__ x 15 = 150 6 x __ = 2 300 ÷ 60 = __ 10 x __ = 60 300 ÷ 150 = __
2 ÷ 6 = __ 1/2 x __ = 1/4 20 ÷ 1/4 = __ 1/2 x 2 = __ 5 x __ = 5
1/2 x __ = 5 __ x 2 + 20 1/4 __ = 5 4 ÷ 4/5 = __ 4/5 x __ = 20
16 ÷ 20 = 4 x __ = 16 25 x __ = 4 4/5 ÷ 5 = __
Courtesy GHWheatley: Coming to Know NumberCourtesy GHWheatley: Coming to Know Number

15. This powerpoint made possible through NRLC with funding
from AB ED and collaboration with Thinking 101
Another type of practice thatAnother type of practice that
focuses on relationships……focuses on relationships……

16. This powerpoint made possible through NRLC with funding
from AB ED and collaboration with Thinking 101
3030 1818
How many ways can you make itHow many ways can you make it
balance?balance?

17. This powerpoint made possible through NRLC with funding
from AB ED and collaboration with Thinking 101
30 18
15 + 15 = 30 so 18 + 12 must15 + 15 = 30 so 18 + 12 must
be 30be 30
Take ten from the 30 and add 2Take ten from the 30 and add 2
to the 18 now you have 20 = 20to the 18 now you have 20 = 20
18 + 2 = 20 and 10 more equals18 + 2 = 20 and 10 more equals
3030
30 – 10 = 20 and 20 –2 = 18 so30 – 10 = 20 and 20 –2 = 18 so
remove 12 from the 30remove 12 from the 30

18. This powerpoint made possible through NRLC with funding
from AB ED and collaboration with Thinking 101
Balances are used toBalances are used to
practice basic addition andpractice basic addition and
subtractions in a way thatsubtractions in a way that
prepares students forprepares students for
algebraic thinking…algebraic thinking…

19. This powerpoint made possible through NRLC with funding
from AB ED and collaboration with Thinking 101
What is the AlgebraicWhat is the Algebraic
Equation ?Equation ?
? ? ? 55
3232

20. This powerpoint made possible through NRLC with funding
from AB ED and collaboration with Thinking 101
3 times n + 5 = 323 times n + 5 = 32
? ? ? 55
3232
What is the AlgebraicWhat is the Algebraic
Equation ?Equation ?

21. This powerpoint made possible through NRLC with funding
from AB ED and collaboration with Thinking 101
Conceptual Understanding:Conceptual Understanding:
When I understand I can transfer and applyWhen I understand I can transfer and apply
my knowledge to new situations. I retainmy knowledge to new situations. I retain
information longer and I enjoy the learninginformation longer and I enjoy the learning
much more. A positive attitude translatesmuch more. A positive attitude translates
directly into higher achievement.directly into higher achievement.

22. This powerpoint made possible through NRLC with funding
from AB ED and collaboration with Thinking 101
A focus on understanding meansA focus on understanding means
“Less Breadth, More Depth“Less Breadth, More Depth ””
Less content at each grade allows students toLess content at each grade allows students to
develop a real understanding of the basics anddevelop a real understanding of the basics and
time to practice and apply those basics in genuinetime to practice and apply those basics in genuine
situations.situations.

23. This powerpoint made possible through NRLC with funding
from AB ED and collaboration with Thinking 101
A fundamental understanding thatA fundamental understanding that
students must gain, Grades 4 tostudents must gain, Grades 4 to
6, is that multiplication is much6, is that multiplication is much
more than just addition.more than just addition.
So you will see strategies forSo you will see strategies for
multiplication facts that are builtmultiplication facts that are built
on models of arrays….on models of arrays….

24. This powerpoint made possible through NRLC with funding
from AB ED and collaboration with Thinking 101
Area models (arrays) create images forArea models (arrays) create images for
multiplication that allow students tomultiplication that allow students to
understand the commutative property.understand the commutative property.
6 x 56 x 5 ==

25. This powerpoint made possible through NRLC with funding
from AB ED and collaboration with Thinking 101
6 x 56 x 5 = 5 x 6= 5 x 6
All I do is turn itAll I do is turn it

26. This powerpoint made possible through NRLC with funding
from AB ED and collaboration with Thinking 101
I can use areaI can use area
models to relatemodels to relate
facts to facts.facts to facts.
Double 6 x 5 solves 12 x 5Double 6 x 5 solves 12 x 5
6 x 5 6 x 5

27. This powerpoint made possible through NRLC with funding
from AB ED and collaboration with Thinking 101
I can use areaI can use area
models to createmodels to create
“families” of facts“families” of facts
6 x 6 + 6 = 7 x 66 x 6 + 6 = 7 x 6
6 x 6

28. This powerpoint made possible through NRLC with funding
from AB ED and collaboration with Thinking 101
I can use areaI can use area
models to solvemodels to solve
factsfacts
9 x 8 = 4 x 8 + 4 x 8 + 1 x 89 x 8 = 4 x 8 + 4 x 8 + 1 x 8
so 9 x 8 = 32 + 32 + 8so 9 x 8 = 32 + 32 + 8
99
88

29. This powerpoint made possible through NRLC with funding
from AB ED and collaboration with Thinking 101
5 groups of 65 groups of 6
equals 30equals 30
I can use area models toI can use area models to
relate multiplication torelate multiplication to
division…division…

30. This powerpoint made possible through NRLC with funding
from AB ED and collaboration with Thinking 101
If you can multiply, you can divideIf you can multiply, you can divide
If 5 groups of 6If 5 groups of 6
equals 30 then 30equals 30 then 30
ddividedivided into 5into 5
equal groupsequal groups
would be 6 in eachwould be 6 in each
group.group.
55
66 3030

31. This powerpoint made possible through NRLC with funding
from AB ED and collaboration with Thinking 101
Or 6 groups of 5,Or 6 groups of 5,
if you pulled itif you pulled it
apart the otherapart the other
way…way…
55
66 3030

32. This powerpoint made possible through NRLC with funding
from AB ED and collaboration with Thinking 101
5 x 6 = 305 x 6 = 30
6 x 5 = 306 x 5 = 30
3030 ÷ 5 = 6÷ 5 = 6
3030 ÷ 6 = 5÷ 6 = 5
55
66
3030
Can you see it??Can you see it??

33. This powerpoint made possible through NRLC with funding
from AB ED and collaboration with Thinking 101
Studying strategies for howStudying strategies for how
multiplication facts are relatedmultiplication facts are related
builds problem solving andbuilds problem solving and
reasoning skills that link to algebra.reasoning skills that link to algebra.
Cut out a 6 times 5 arrayCut out a 6 times 5 array

34. This powerpoint made possible through NRLC with funding
from AB ED and collaboration with Thinking 101
This is a 6 x 5, turn it... It is still a 6 x 5This is a 6 x 5, turn it... It is still a 6 x 5
but now you might label it a 5 x 6but now you might label it a 5 x 6
(especially if you are measuring for windows and doors)(especially if you are measuring for windows and doors)
6 x 5 = 5 x 66 x 5 = 5 x 6

35. This powerpoint made possible through NRLC with funding
from AB ED and collaboration with Thinking 101
Cut it apart to see 6 is broken into 2 and 4. WhenCut it apart to see 6 is broken into 2 and 4. When
you put it back together you can “see” to record theyou put it back together you can “see” to record the
equation.equation.
6 x 5 = (2 x 5) + (4 x 5) or (2+4) x 56 x 5 = (2 x 5) + (4 x 5) or (2+4) x 5
55
2 +2 +
44
55

36. This powerpoint made possible through NRLC with funding
from AB ED and collaboration with Thinking 101
Do you understand my sketch?.Do you understand my sketch?.
6 x 5 = (2 x 5) + (4 x 5)6 x 5 = (2 x 5) + (4 x 5)
Or (2+4) x 5Or (2+4) x 5
2 x 52 x 5 4 x 54 x 5
6 = 2 + 46 = 2 + 4
55

37. This powerpoint made possible through NRLC with funding
from AB ED and collaboration with Thinking 101
Cut it apart in four pieces, then put itCut it apart in four pieces, then put it
together and record the equation.together and record the equation.
22
5 = +5 = +
33
6 = 2 +6 = 2 +
44
(2 x 2 ) + (4 x 2) + (3 x 2) +(3 x 4) = 6 x 5(2 x 2 ) + (4 x 2) + (3 x 2) +(3 x 4) = 6 x 5

38. This powerpoint made possible through NRLC with funding
from AB ED and collaboration with Thinking 101
Do you understand my sketch?Do you understand my sketch?
2 x 22 x 2
4 x 24 x 2
2 x 32 x 3 4 x 34 x 3
2 + 42 + 4
22
++
33
(2 x 2 ) + (4 x 2) + (3 x 2) +(3 x 4) = 6 x 5(2 x 2 ) + (4 x 2) + (3 x 2) +(3 x 4) = 6 x 5

39. This powerpoint made possible through NRLC with funding
from AB ED and collaboration with Thinking 101
44 88
66 1212
2 + 42 + 4
22
++
33
(2 x 2 ) + (4 x 2) + (3 x 2) +(3 x 4) = 6(2 x 2 ) + (4 x 2) + (3 x 2) +(3 x 4) = 6
x 5x 5
6 x 5 = 10 + 206 x 5 = 10 + 20

40. This powerpoint made possible through NRLC with funding
from AB ED and collaboration with Thinking 101
You just performed the distributiveYou just performed the distributive
property..property..
A number property that is criticalA number property that is critical
to understanding multi digitto understanding multi digit
multiplication and division as well asmultiplication and division as well as
algebra.algebra.

41. This powerpoint made possible through NRLC with funding
from AB ED and collaboration with Thinking 101
The move to two digit multiplication:The move to two digit multiplication:
On grid paper draw an area model that would cover a 15 xOn grid paper draw an area model that would cover a 15 x
14 area.14 area.
15 = 10 +15 = 10 +
55
1414
==
1010
++
44

42. This powerpoint made possible through NRLC with funding
from AB ED and collaboration with Thinking 101
1010
++
44
10 + 510 + 5
100100
2020
5050
4040

43. This powerpoint made possible through NRLC with funding
from AB ED and collaboration with Thinking 101
100100 5050
4040 2020
10 + 510 + 5
1010
++
44
Represent what you built in a matrixRepresent what you built in a matrix

44. This powerpoint made possible through NRLC with funding
from AB ED and collaboration with Thinking 101
You can add it two ways !!!You can add it two ways !!!
100100 5050
4040 2020
10 + 510 + 5
1010
++
44
150150
6060
110110
140140 70 = 11070 = 110

45. This powerpoint made possible through NRLC with funding
from AB ED and collaboration with Thinking 101
4040
++
77
30 + 630 + 6
Try 36 xTry 36 x
4747

46. This powerpoint made possible through NRLC with funding
from AB ED and collaboration with Thinking 101
4040
++
77
30 + 630 + 6
30 + 630 + 6
240240
4242
12001200
210210
4040
++
77
I can see it!!I can see it!!
14401440
252252

47. This powerpoint made possible through NRLC with funding
from AB ED and collaboration with Thinking 101
240240
4242
12001200
210210
30 + 630 + 6
4040
++
77
14401440
252252
3636
XX 4747
4242
210210
2424
12001200
3636
XX 4747
252252
14401440
They all result in the sameThey all result in the same
set of numbers being addedset of numbers being added
together!!!together!!!

48. This powerpoint made possible through NRLC with funding
from AB ED and collaboration with Thinking 101
xyxy
yy22
xx22
xyxy
x + yx + y
xx
++
yy
Area models link right to highArea models link right to high
school….school….
xx22
+ xy + xy ++ xy + xy + yy22
oror
xx22
+ 2xy ++ 2xy + yy22

49. This powerpoint made possible through NRLC with funding
from AB ED and collaboration with Thinking 101
Students develop Personal Strategies forStudents develop Personal Strategies for
CalculatingCalculating
When I understand I can build formulas and
procedures that make sense to me. When I practice
my ways of thinking, I become fluent and accurate.
Instead of trying to remember “the rules” I can
explain and justify solutions.

50. This powerpoint made possible through NRLC with funding
from AB ED and collaboration with Thinking 101
Practice with area models leads toPractice with area models leads to
fluency with multiplication and divisionfluency with multiplication and division
based on understanding…..based on understanding…..
Grade 4 student:Grade 4 student:
To remember 7 x 8, I say 5 x 8 = 40 and 2 moreTo remember 7 x 8, I say 5 x 8 = 40 and 2 more
8’s is 16 so 7 x 8 = 56.8’s is 16 so 7 x 8 = 56.
She records the answer as quickly as the student whoShe records the answer as quickly as the student who
just memorized, but she has an understanding that willjust memorized, but she has an understanding that will
lead her to algebra with ease.lead her to algebra with ease.

51. This powerpoint made possible through NRLC with funding
from AB ED and collaboration with Thinking 101
Students who have practicedStudents who have practiced
taking apart and putting togethertaking apart and putting together
numbers are not afraid to think innumbers are not afraid to think in
problem solving situations…problem solving situations…

52. This powerpoint made possible through NRLC with funding
from AB ED and collaboration with Thinking 101
Can I share 136 candiesCan I share 136 candies
with 6 people?with 6 people?
I know 6 x 6 is 36 so they each get 6. Now there isI know 6 x 6 is 36 so they each get 6. Now there is
100 to share. I went from 12 x 6 is 72 in my head to100 to share. I went from 12 x 6 is 72 in my head to
add 2 more 12, then 2 more 12 so 96 is as close as Iadd 2 more 12, then 2 more 12 so 96 is as close as I
can get. That means 12 plus 4 more or 16 sixes. Ican get. That means 12 plus 4 more or 16 sixes. I
checked with multiplication and 6 times 16 is 96. Sochecked with multiplication and 6 times 16 is 96. So
they each get 22.they each get 22.

53. This powerpoint made possible through NRLC with funding
from AB ED and collaboration with Thinking 101
I understandI understand
what 1/3 andwhat 1/3 and
1/4 mean in1/4 mean in
terms of parts ofterms of parts of
a set.a set.
I know 1/3 in myI know 1/3 in my
head. If it was 75head. If it was 75
it would be 25it would be 25
each, but it is 3each, but it is 3
less so 24 each.less so 24 each.
I know 1/4 by 36I know 1/4 by 36
and 36 andand 36 and
halving so 18halving so 18

54. This powerpoint made possible through NRLC with funding
from AB ED and collaboration with Thinking 101
Problem solving should be the focus ofProblem solving should be the focus of
mathematics at all levels.mathematics at all levels.
The answersThe answers mattersmatters because you canbecause you can
explain how and why you know it is theexplain how and why you know it is the
answer.answer.

55. This powerpoint made possible through NRLC with funding
from AB ED and collaboration with Thinking 101
Personal StrategiesPersonal Strategies
• Teachers provide opportunities for students to
represent their thinking in a variety of ways rather
than prescribing how students will record
mathematics symbolically.
• This allows every student to build understanding
• Students compare approaches and solutions to
discover why they work.

56. This powerpoint made possible through NRLC with funding
from AB ED and collaboration with Thinking 101
As parents,As parents,
Ask your child to explain how he or she is thinkingAsk your child to explain how he or she is thinking
Listen carefully and ask your child to help you understandListen carefully and ask your child to help you understand
Ask your child to show you how they are breaking the numbers apart.Ask your child to show you how they are breaking the numbers apart.
Fight the desire to show an “easy way”. Our goal is to engage them inFight the desire to show an “easy way”. Our goal is to engage them in
thinking, that is hard work and it takes time..thinking, that is hard work and it takes time..
Trust that if they practice thinking, practice taking apart and puttingTrust that if they practice thinking, practice taking apart and putting
together numbers, they will gain a deep, rich understanding thattogether numbers, they will gain a deep, rich understanding that
carries them right through to algebra and beyond.carries them right through to algebra and beyond.

57. This powerpoint made possible through NRLC with funding
from AB ED and collaboration with Thinking 101
As parents,As parents,
You will see less homework as much of this work has to be doneYou will see less homework as much of this work has to be done
actively with all students discussing and debating.actively with all students discussing and debating.
If work comes home that you do not understand, tell the teacher youIf work comes home that you do not understand, tell the teacher you
were not able to help with the homework.were not able to help with the homework.
Do not show an “easier” way, showing your way shuts down studentDo not show an “easier” way, showing your way shuts down student
thinking.thinking.
Trust that every teacher wants every child to be successful. We wantTrust that every teacher wants every child to be successful. We want
children to feel confident, to trust their own abilities to think, tochildren to feel confident, to trust their own abilities to think, to
problem solve, to know that it takes time and patience to learn toproblem solve, to know that it takes time and patience to learn to
understand.understand.

58. This powerpoint made possible through NRLC with funding
from AB ED and collaboration with Thinking 101
Why not just learn “the rules?”Why not just learn “the rules?”
• When children are told to just follow rules, before they have theWhen children are told to just follow rules, before they have the
foundational ideas necessary to understand the mathematicsfoundational ideas necessary to understand the mathematics
present in the problems, they try to memorize steps for getting thepresent in the problems, they try to memorize steps for getting the
right answers. It works for a while. But breaks down at the pointright answers. It works for a while. But breaks down at the point
when true understanding becomes necessary for further growth.when true understanding becomes necessary for further growth.
• By Junior High many give up or stop thinking and just try to getBy Junior High many give up or stop thinking and just try to get
through.through.
They stop looking for meaning and decide mathematics is notThey stop looking for meaning and decide mathematics is not
supposed to make sense.supposed to make sense.

59. This powerpoint made possible through NRLC with funding
from AB ED and collaboration with Thinking 101
Frequently Asked QuestionsFrequently Asked Questions
• I hated math in school and can’t do it. My oldest son was doing great at it, butI hated math in school and can’t do it. My oldest son was doing great at it, but
now hates this new math with all the problem solving. He gets so frustratednow hates this new math with all the problem solving. He gets so frustrated
when he does his homework. How can I help him?when he does his homework. How can I help him?
– Keep a positive attitude, build confidence. It is important that he hears
that you believe that he will learn how to do it.
– Develop persistence and be patient – it takes time to teach students
how to think, reason, explain, use different strategies.
– Ask questions: How did you do that? Can you explain that? Can you
try another way? What do we know? What do we have to find out?
Have you done another problem like this one?

60. This powerpoint made possible through NRLC with funding
from AB ED and collaboration with Thinking 101
Basic facts are not being practiced. How can anyone do any math if theyBasic facts are not being practiced. How can anyone do any math if they
haven’t memorized the basic facts?haven’t memorized the basic facts?
• Basic facts are being practiced daily but not drilled and timed.
• Along with being accurate, it is critical that students understand the concepts and develop
number sense. If students don’t know the relationships between numbers, they will not
develop accuracy and efficiency when working with numbers.
• There is no race to see who gets finished fastest. Timed tests develop anxiety not accuracy.
Timed tests will be removed from the PATs (Provincial Achievement Tests) in grades 3 and 6.
• It takes time to learn concepts, and understand relationships between numbers.
• Some students find memorization very difficult, some students find explaining their answers
very difficult. Memorizing without understanding doesn’t last. It must make sense, then they
will remember it. It takes time to find personal strategies that they understand and can use.
The new program recognizes this by having grade K – 9 slowly develop the same concepts.

61. This powerpoint made possible through NRLC with funding
from AB ED and collaboration with Thinking 101
Universities and high schools keep saying that students are arriving with fewer andUniversities and high schools keep saying that students are arriving with fewer and
fewer skills all the time. How will this program address this?fewer skills all the time. How will this program address this?
• It is important that we teach students how to make sense of information and how to work
persistently to solve real life problems.
• In Kindergarten to grade 9, students are taught how to think and reason to understand concepts
and to make sense of mathematical ideas. Students develop personal strategies to solve
problems. Students will be more prepared to handle the more complex and abstract concepts in
junior and senior high.
• As adults, most of the math we use is mental mathematics and estimation. We use math for
shopping, reviewing bank and credit card statements, paying bills, etc. If we need one, a
calculator is always near by. Should we spend 4 years of school drilling students how to do
long division by hand? Students need to understand it, know when to use it, and estimate a
reasonable answer.
• Geometry and measurement are equally important as an adult when following directions, buying
rugs and paint, assembling BBQs, furniture, building decks, doing repairs,etc.
• Data analysis and identifying patterns also important to make sense of data and make valid
interpretations of the huge amount of information we have available today.

62. This powerpoint made possible through NRLC with funding
from AB ED and collaboration with Thinking 101
2007 K – 9 Mathematics Program2007 K – 9 Mathematics Program
• The goal is to prepare our students to:
– Use math confidently to solve problems
– Reason and communicate mathematically
– Appreciate and value mathematics
– Make connections between mathematics and its applications
– Commit themselves to life long learning
– Become mathematically literate adults using mathematics to contribute to
society
• It’s a big goal, but very attainable – with your help. Parents play a huge role in
their child’s education. By encouraging a positive attitude, building persistence,
strategizing in games, discussing with your child real life applications of math
skills, your child will truly succeed.