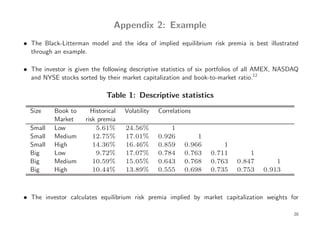
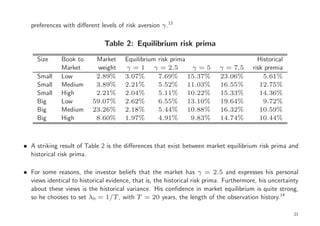
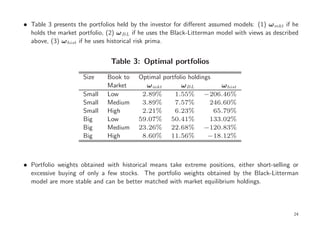
The document discusses the Black-Litterman model in the context of Bayesian portfolio analysis, exploring how parameter uncertainty affects financial decision-making. It emphasizes the integration of market equilibrium risk premia with investors' subjective views on asset returns, highlighting the advantages of using the mixed estimation model. The Black-Litterman model enhances portfolio stability by enabling investors to incorporate non-sample information, contrasting with traditional portfolio selection based solely on past observations.

1. Lecture Notes
The Black-Litterman model in the light of Bayesian
portfolio analysis
Parameter Uncertainty and Learning in Dynamic
Financial Decisions
Daniel A. Bruggisser
December 1, 2010

2. Agenda
1. Introduction
2. Bayesian portfolio analysis
3. The mixed estimation model
4. The Black-Litterman model
5. Relating the Black-Litterman model to shrinkage estimation
6. Conclusion
2

3. Introduction
• Parameter uncertainty is ubiquitous in finance.
• Given that the observation history is rarely a good predictor of the future and that
certain parameters such as the mean of asset returns are difficult to estimate with
precision, it is evident that information other than the sample statistics of past
observations may be very useful in a portfolio selection context.
• Such non-sample information may include fundamental analysis and the beliefs in
a certain economic model such as market efficiency or equilibrium pricing.
• The Black-Litterman model is an application of Bayesian mixed estimation. It is
deeply rooted in the theory of Bayesian analysis.
• The Balck-Litterman model allows the investor to combine two sources of infor-
mation: (1) The market equilibrium risk prima; (2) The investors subjective views
about some of the assets return forecasts.
3

4. Bayesian Portfolio Analysis
• The classical portfolio selection problem:1
max ET [U (WT +1)] = max U (WT +1)p(rT +1|θ)drT +1 (1)
ω ω Ω
f f
s.t. WT +1 = WT ω ′ exp(rT +1 + rT ) + (1 − ι′ω) exp(rT ) , (2)
where Ω is the sample space, U (WT +1) is a utility function, WT +1 is the wealth
at time T + 1, θ is a set parameters, ω are portfolio weights, p(rT +1|θ) is the
f
sample density of returns, rT is the risk free rate, and ι is a vector of ones. The
column vectors ι, ω and rT +1 are of the same dimension.
• The parameter vector θ is assumed to be known to the investor. However, some
parameters are estimates and subject to parameter uncertainty.
4

5. • Bayesian portfolio selection problem:2
max ET [U (WT +1)] = max U (WT +1)p(rT +1|ΦT )drT +1, (3)
ω ω Ω
f f
s.t. WT +1 = WT ω ′ exp(rT +1 + rT ) + (1 − ι′ω) exp(rT ) , (4)
where ΦT is the information available up to time T , and p(rT +1|ΦT ) is the
Bayesian predictive distribution (density) of asset returns.
• Conditioning takes place on ΦT instead of essentially uncertain parameters θ.
• There are many ways to derive the Bayesian predictive distribution depending on
the model at hand, the choice of the prior distribution of uncertain quantities, and
the information the investor assumes as known.
5

6. • Bayesian decomposition, Bayes′ rule and Fubini′s theorem:3
ET [U (WT +1)] = U (WT +1)p(rT +1|ΦT )drT +1 (5)
Ω
= U (WT +1)p(rT +1, θ|ΦT )d(drT +1, θ)
Ω×Θ
= U (WT +1)p(rT +1|θ)p(θ|ΦT )dθdrT +1
Ω Θ
= U (WT +1) p(rT +1|θ)p(ΦT |θ)p(θ)dθ drT +1,
Ω Θ
where Θ is the parameter space, p(rT +1, θ|ΦT ) is the joint density of parameters
and realizations, p(θ|ΦT ) is the posterior density, p(ΦT |θ) is the conditional
likelihood, and p(θ) is the prior density of the parameters.
6

7. The mixed estimation model
• Mixed estimation allows the investor to combine different sources of information.4
Let the sample density of returns be given a multivariate normal density
p(rt|µ, Σ) = N µ, Σ , (6)
and assume that the prior density for the m × 1 vector of means µ also has
multivariate normal density with
p(µ) = N (m0, Λ0) . (7)
The investor expresses views about µ by imposing
p(v|µ) = N (Pµ, Ω) , (8)
where P is an n×m design matrix that selects and combines returns into portfolios
about which the investor is able to express his views. v is a n × 1 vector of views
and the n × n matrix Ω expresses the uncertainty of those views.
7

8. Applying Bayes′ rule, the posterior of µ given the investors views v is then
p(µ|v) ∝ p(v|µ)p(µ). (9)
It emerges that the posterior of µ updated by the views v is (see Appendix 1 for
a proof)
p(µ|v) = N (mv , Λv ) (10)
−1
mv = Λ−1 + P′Ω−1 P
0 Λ−1 m0 + P′Ω−1v
0
−1
Λv = Λ−1 + P′Ω−1 P
0 .
Then, the predictive density of one period ahead returns is obtained by integrating
over the unknown parameter µ
p(rT +1|v, Σ) = p(rT +1|µ, Σ)p(µ|v)dµ, (11)
Θ
8

9. which can be shown to result in (see Appendix 1 for a proof)
p(rT +1|v, Σ) = N mv , Σ + Λv . (12)
An interesting effect of parameter uncertainty is that in the long-run (buy-and-hold
investor), assets are viewed riskier than at short-sight. It can be shown that the
k-period predictive density is (see Appendix 1 for a proof)
p(rT +k |v, Σ) = N (kmv , kΣ + k 2Λv ). (13)
This effect of parameter uncertainty has first been noted by Barberis (2000).
9

10. Black-Litterman model
• The Black-Litterman model
Black & Litterman (1992) suggest using the market equilibrium model as a prior
obtained by reverse optimization5
µequ = γΣω ∗ ,
mkt (14)
where γ is the risk aversion of a power utility investor and ω ∗ are the market
mkt
portfolio weights (fractions of the market capitalization). Black & Litterman
assume a natural conjugate prior for the vector of means such that
p(µ) = N µequ, λ0Σ . (15)
The investor expresses views about µ by imposing
p(v|µ) = N (Pµ, Ω) . (16)
10

11. It follows that the posterior of µ updated by the views is
p(µ|v) = N (mv , Λv ) (17)
−1
−1 −1 −1
mv = (λ0Σ) ′
+PΩ P (λ0Σ) µequ + P′ Ω−1v (18)
−1
−1 ′ −1
Λv = (λ0Σ) +PΩ P . (19)
Then, the Bayesian predictive density of one period ahead returns is obtained by
the same argument as in mixed estimation (see Appendix 1 for a proof)6
p(rT +1|v, Σ) = N mv , Σ + Λv (20)
and the k-period predictive density is again
p(rT +k |v, Σ) = N (kmv , kΣ + k 2Λv ). (21)
• An example of the Black-Litterman model is given in Appendix 2.
11

12. Relating the Black-Litterman model to shrinkage estimation
• The Black-Litterman model can be aligned to shrinkage estimation by matrix
algebra.7
If P and Ω are m × m with full rank (n = m), and v is an m × 1 vector, the
mean of the posterior in (18) can be written in shrinkage form:
µv = δµequ + (I − δ)(P′P)−1 P′v, (22)
where I is an m × m identity matrix with principal diagonal elements of one and
zero elsewhere. δ is called the posterior shrinkage factor. It can be shown that8
−1
−1
δ = (λ0Σ) ′
+PΩ −1
P (λ0Σ)−1 (23)
−1
= [prior covariance]−1 + [conditional covariance]−1 [prior covariance]−1
= [posterior covariance][prior covariance]−1.
12

13. Conclusion (1)
• Bayesian portfolio analysis has a long tradition in finance.
• Given that the observation history is rarely a good predictor of the future, it is
evident that information other than the sample statistics of past observations may
be very useful in a portfolio selection context.
• Furthermore, portfolio choices are by nature subjective decisions and not objective
inference problems as the mainstream literature on portfolio choice might suggest.
Therefore, there is no need to facilitate comparison.9
• The mixed estimation model and the Black-Litterman model in particular allow
the investor to combine different sources of information.
• If the investor uses the market equilibrium risk prima as a prior, the mixed
estimation model is the Black-Litterman model.
13

14. • Portfolios constructed from Black-Litterman model exhibit overall more stability
in the optimal allocation decision compared to the case where sample statistics
are used.
14

15. Appendix 1: Proof of mixed estimation
• Derivation of the posterior
The proof follows Satchell & Scowcroft (2000), Scowcroft & Sefton (2003), and Theil & Goldberger
(1961). The prior on the m × 1 vector of means µ is multivariate normal such that
p(µ) = N (m0 , Λ0) (24)
where m0 is a m × 1 vector and Λ0 is a m × m and matrix assumed non-singular. In explicit
form, the prior can be written as
−m/2 −1/2 1 ′ −1
p(µ) = (2π) |Λ0 | exp − (µ − m0) Λ0 (µ − m0 ) (25)
2
−m/2 −1/2 1 ′ −1 ′ −1 1 ′ −1
= (2π) |Λ0 | exp − µ Λ0 µ + µ Λ0 m0 − µ0Λ0 µ0 (26)
2 2
1
∝ exp − µ′Λ−1µ + µ′Λ−1m0
0 0 . (27)
2
The probability density of the views is also multivariate normal
p(v|µ) = N (Pµ, Ω) (28)
15

16. where P is a n × m design matrix and Ω is an n × n matrix. n is the number of views and m
the number of assets. The explicit form of the views probability is
−1/2 1
p(v|µ) = (2π)−m/2 |Ω| exp − (v − Pµ)′ Ω−1(v − Pµ) (29)
2
1 ′ ′ −1 ′ ′ −1
∝ exp − µ (P Ω P)µ + µ (P Ω v) . (30)
2
Combining (27) and (30) using Bayes’ rule
p(µ|v) ∝ p(v|µ)p(µ) (31)
gives
1
p(µ|v) ∝ exp − µ′(P′ Ω−1P)µ + µ′(P′ Ω−1v) ×
2
1
exp − µ′Λ−1µ + µ′Λ−1m0
0 0 , (32)
2
which implies that the distribution of µ conditional on the views v is also multivariate normal.
16

17. Collecting terms in (32), it follows that
p(µ|v) = N (mv , Λv ) (33)
−1
−1 ′ −1 −1 ′ −1
mv = Λ0 +PΩ P Λ0 m0 + P Ω v (34)
−1
−1 ′ −1
Λv = Λ0 + P Ω P . (35)
• Derivation of the shrinkage form
If P and Ω are m × m with full rank (n = m), and v is an m × 1 vector, the above posterior
can be brought into shrinkage form by expanding the last term in (34) by P(P′P)−1 P′. Then10
−1
−1 ′ −1 −1 ′ −1 ′ −1 ′
mv = Λ0 +PΩ P Λ0 m0 + P Ω P(P P) Pv (36)
has shrinkage form and can be written11
mv = δ m0 + (I − δ)(P′ P)−1P′v (37)
−1
−1 ′ −1 −1
δ = Λ0 +PΩ P Λ0 . (38)
17

18. • Derivation of the Bayesian predictive density
The Bayesian predictive density of one period ahead returns is obtained by integrating over the
unknown parameter µ
p(rT +1 |v, Σ) = p(rT +1 |µ, Σ)p(µ|v)dµ, (39)
Θ
which can be shown to result in
p(rT +1 |v, Σ) = N mv , Σ + Λv . (40)
We can avoid the tedious effort of integration by making use of the well known properties of
multivariate normal densities. Note that p(rT +1 |µ, Σ) = N µ, Σ) and p(µ|v) = N (mv , Λv ).
Therefore, the partitioned matrix for the joint movement of rT +1 and µ is
µ mv Λv H12
v, Σ ∼ N , . (41)
rT +1 mv H21 H22
The following equality must hold for the mean of the conditional density p(rT +1 |µ, Σ)
µ ≡ mv + H21 Λ−1(µ − mv )
v (42)
18

19. and therefore H21 = Λv . By symmetry of the covariance H12 = Λv . Furthermore, because
−1
Σ ≡ H22 − Λv Λv Λv (43)
it is clear that H22 = Σ + Λv
The complete partitioned matrix is then (Bauwens, Lubrano & Richard, 1999, p. 300)
µ mv Λv Λv
v, Σ ∼ N , . (44)
rT +1 mv Λv Σ + Λv
and therefore
p(rT +1 |v, Σ) = N mv , Σ + Λv . (45)
• k-period predictiv density. The argument is that the k-period sample density is p(rT +k |µ, Σ) =
N (kµ, kΣ) and the posterior density of µ is given by p(µ|v) = N (mv , Λv ), then, the Bayesian
predictive density is obtained from solving the integral
p(rT +k |v, Σ) = p(rT +k |µ, Σ)p(µ|v)dµ. (46)
Θ
It can be shown by the same argument as for the one period case, that the k-period predictive
density
p(rT +k |v, Σ) = N (kmv , kΣ + k2 Λv ). (47)
19

20. Appendix 2: Example
• The Black-Litterman model and the idea of implied equilibrium risk premia is best illustrated
through an example.
• The investor is given the following descriptive statistics of six portfolios of all AMEX, NASDAQ
and NYSE stocks sorted by their market capitalization and book-to-market ratio.12
Table 1: Descriptive statistics
Size Book to Historical Volatility Correlations
Market risk premia
Small Low 5.61% 24.56% 1
Small Medium 12.75% 17.01% 0.926 1
Small High 14.36% 16.46% 0.859 0.966 1
Big Low 9.72% 17.07% 0.784 0.763 0.711 1
Big Medium 10.59% 15.05% 0.643 0.768 0.763 0.847 1
Big High 10.44% 13.89% 0.555 0.698 0.735 0.753 0.913
• The investor calculates equilibrium risk premia implied by market capitalization weights for
20

21. preferences with different levels of risk aversion γ .13
Table 2: Equilibrium risk prima
Size Book to Market Equilibrium risk prima Historical
Market weight γ = 1 γ = 2.5 γ=5 γ = 7.5 risk premia
Small Low 2.89% 3.07% 7.69% 15.37% 23.06% 5.61%
Small Medium 3.89% 2.21% 5.52% 11.03% 16.55% 12.75%
Small High 2.21% 2.04% 5.11% 10.22% 15.33% 14.36%
Big Low 59.07% 2.62% 6.55% 13.10% 19.64% 9.72%
Big Medium 23.26% 2.18% 5.44% 10.88% 16.32% 10.59%
Big High 8.60% 1.97% 4.91% 9.83% 14.74% 10.44%
• A striking result of Table 2 is the differences that exist between market equilibrium risk prima and
historical risk prima.
• For some reasons, the investor beliefs that the market has γ = 2.5 and expresses his personal
views identical to historical evidence, that is, the historical risk prima. Furthermore, his uncertainty
about these views is the historical variance. His confidence in market equilibrium is quite strong,
so he chooses to set λ0 = 1/T , with T = 20 years, the length of the observation history.14
21

22. • The views of the investor translate into the following matrices:
   
1 0 0 0 0 0 0.0561

 0 1 0 0 0 0 


 0.1275 

0 0 1 0 0 0 0.1436
   
P= , v= (48)
   
0 0 0 1 0 0 0.0972

   
0 0 0 0 1 0 0.1059
   
   
0 0 0 0 0 1 0.1044
 
0.0603 0 0 0 0 0

 0 0.0289 0 0 0 0 

0 0 0.0271 0 0 0
 
Ω= (49)
 
0 0 0 0.0291 0 0

 
0 0 0 0 0.0227 0
 
 
0 0 0 0 0 0.0193
Using equations (17)-(19), the investor calculates the posterior of µ given the views: With
22

23. equilibrium risk premium µequ and Σ given by
   
0.0769 0.0603 0.0387 0.0347 0.0329 0.0238 0.0189
 0.0552   0.0387 0.0289 0.0270 0.0222 0.0197 0.0165 
   
0.0511  0.0347 0.0270 0.0271 0.0200 0.0189 0.0168
   
µequ = , Σ =  ,
  
 0.0655   0.0329 0.0222 0.0200 0.0291 0.0218 0.0179 
0.0544  0.0238 0.0197 0.0189 0.0218 0.0227 0.0191
   
  
0.0491 0.0189 0.0165 0.0168 0.0179 0.0191 0.0193
the posterior is p(µ|v) = N (mv , Λv ) with
   
0.0901 0.0025 0.0016 0.0014 0.0013 0.0009 0.0007

 0.0657 


 0.0016 0.0012 0.0011 0.0009 0.0008 0.0006 

0.0614 0.0014 0.0011 0.0011 0.0008 0.0007 0.0007
   
µv =  , Λv =  .
   
 0.0751   0.0013 0.0009 0.0008 0.0012 0.0009 0.0007 
0.0638 0.0009 0.0008 0.0007 0.0009 0.0009 0.0008
   
   
0.0542 0.0007 0.0006 0.0007 0.0007 0.0008 0.0008
The investor then calculates his optimal portfolio holdings implied by the Bayesian predictive
distribution
p(rT +1 |v, Σ) = N (mv , Σ + Λv ) (50)
23

24. • Table 3 presents the portfolios held by the investor for different assumed models: (1) ω mkt if he
holds the market portfolio, (2) ω BL if he uses the Black-Litterman model with views as described
above, (3) ω hist if he uses historical risk prima.
Table 3: Optimal portfolios
Size Book to Optimal portfolio holdings
Market ω mkt ω BL ω hist
Small Low 2.89% 1.55% −206.46%
Small Medium 3.89% 7.57% 246.60%
Small High 2.21% 6.23% 65.79%
Big Low 59.07% 50.41% 133.02%
Big Medium 23.26% 22.68% −120.83%
Big High 8.60% 11.56% −18.12%
• Portfolio weights obtained with historical means take extreme positions, either short-selling or
excessive buying of only a few stocks. The portfolio weights obtained by the Black-Litterman
model are more stable and can be better matched with market equilibrium holdings.
24

25. Footnotes
1
See, e.g., Campbell & Viceira (2003, p. 22), Barberis (2000).
2
See, e.g., Barberis (2000), Kandel & Stambaugh (1996, p. 388), Rachev et al. (2008, p. 96), Wachter (2007, p. 14).
3
See Barberis (2000), Brandt (2010, p. 308), Brown (1976, 1978), Kandel & Stambaugh (1996, p. 388), Klein & Bawa
(1976), Pstor (2000), Skoulakis (2007, p. 7), and Zellner & Chetty (1965).
4
Mixed estimation is attributed to the work of Theil & Goldberg (1961). It is also presented in Brandt (2010, p. 313),
Satchell & Scowcroft (2000), Scowcroft & Sefton (2003). The Black & Litterman (1992) model is a special case of mixed
estimation.
5
Note that Black & Litterman (1992) assume simple returns. The exact formula for power utility and continuously
compounded excess returns is µequ = γ Σω ∗ 2
mkt − σ /2 (see Campbell & Viceira, 2003, p. 30). The optimal
1−γ
allocation for a power utility investor with U (WT +1 ) = WT +1 /(1 − γ) and continuously compounded excess returns
is ω = γ Σ µ + σ 2 /2 , where σ 2 is the vector of the diagonal elements of Σ. However, for short investment horizon,
1
the optimal allocation will not be significantly different for continuously compounded excess returns.
6
See also Rachev et al. (2008, p. 148).
7
Posterior shrinkage is a generalization of the Bayes-Stein estimator (Jorion, 1986) and is a direct result from
reformulating the posterior obtained by an informative prior in shrinkage form.
8
See, e.g., Greene (2008, p. 607), Hoff (2009, p. 108), Koop, Poirier & Tobias (2007, p. 26).
25

26. 9
See Brandt (2010, p. 311).
10
See Rachev et al. (2008, p. 146).
11
See, e.g., Greene (2008, p. 607), Hoff (2009, p. 108), Koop, Poirier & Tobias (2007, p. 26).
12
The values of the example are taken from Brandt (2010) who uses monthly data from January 1983 through December
2003.
13
The values of the example are taken from Brandt (2010) who uses monthly data from January 1983 through December
2003.
14
See Rachev et al. (2008, p. 147), who also use λ0 = 1/T . Note that the view forecasts are assumed to be
independent. Therefore, Ω is a diagonal matrix.
26