Dokumen ini membahas konsep limit dan kontinuitas dalam kalkulus, termasuk definisi intuitif dan teorema-teorema terkait. Berbagai contoh limit fungsi serta metode untuk menentukan limit ditunjukkan, termasuk faktorisasi dan rasionalisasi. Selain itu, dijelaskan kriteria kontinuitas fungsi dan contoh diskontinuitas.

1. Pertemuan # 4:
Limit dan Kontinuitas
Limit &
KALKULUS - 1
Slide - 1

2. 2.3 Konsep Limit
Definisi Intuitif
Misalkan y=f(x) suatu fungsi, a dan L bilangan riil
sedemikian hingga:
• Bila x dekat a tetapi tidak sama dg a (x≠a), f(x) dekat
ke L
• Bila x mendekati a tetapi x≠a, maka f(x) mendekati L
• Misalkan f(x) dapat kita buat sedekat mungkin ke L dg
membuat x cukup dekat a tetapi tdk sama dg a
• Maka dapat dikatakan bhw limit f(x) bila x mendekati a
adalah L,
lim f ( x ) = L
x →a
Limit &
KALKULUS - 1
Slide - 2

3. Contoh
x2 − 4
4
lim 2
=
x →2 x + x − 6
5
1.
x
f ( x)
x
1
1 .5
1 .9
0.75
0.7778
0.7959
3
2 .5
2.1
0.83333
0.81818
0.80392
1.999
0.79996
2.001
0.80004
↓
2
Limit &
↓
0 .8
↓
2
KALKULUS - 1
f ( x)
↓
0.8
Slide - 3

4. Teorema Limit
Andaikan n bilangan bulat positif, k konstanta, dan f dan g adalah
fungsi-fungsi yang mempunyai limit di c. Maka :
1)
limk = k
x →c
2)
lim x = c
x →c
3)limkf(x) = k
x →c
8)
lim[ f(x)]
x →c
lim f(x)
n
[
]
= lim f(x)
x →c
n
x →c
4)lim [ f(x) + g(x)] = lim f(x) + lim g(x)
x →c
f(x)
lim g(x) = lim f(x)/ lim g(x)
x →c
x →c
x →c
7)
x →c
9)
x →c
lim
n
f(x) = n limf(x)
x →c
5) lim[ f(x) − g(x)] = lim f(x) − lim g(x)
x →c
x →c
x →c
6) lim[ f(x).g(x)] = lim f(x).lim g(x)
x →c
Limit &
x →c
x →c
KALKULUS - 1
Slide - 4

5. Contoh
1)
lim(3x − 2) = 3 lim x − lim 2 = 4
x →2
x →2
x →2
2) lim(x 2 + 2x − 2) = lim x 2 + 2 lim x − lim 2
x →3
x →3
x →3
x →3
= (3)2 + 2(3) − 2 = 9 + 6 − 2 = 13
3)
3 x − 2 lim(3 x − 2) 3 lim x − lim 2
x →2
= x →2
= x →2
lim 9 x + 7 lim(9 x + 7) 9 lim x + lim 7
x →2
x →2
=
Limit &
x →2
x →2
3(2) − 2 6 − 2
4
=
=
9(2) + 7 18 + 7 25
KALKULUS - 1
Slide - 5

6. 4)
lim
x →4
9 + x 2 = lim(9 + x 2 )
x →4
= (9 + 4 2 ) = 25 = 5
5)
(x + h)2 − x 2
(x 2 + 2hx + h2 − x 2 )
2hx + h2
= lim
= lim(2x + h) = 2x
= lim
lim
h →0
h →0
h →0
h
h
h
h →0
6) lim(2 x + 3)( x − 2) = lim(2 x + 3). lim( x − 2)
x →1
x →1
x →1
= (2.1 + 3).(1 − 2) = 5.(−1) = −5
Limit &
KALKULUS - 1
Slide - 6

7. Limit Fungsi
1)
Beberapa limit fungsi yang istimewa, yaitu :
1)
lim
sin x
x
x →0
2)
3)
=1
untuk x kecil maka sin x ≈ x
x
lim sinx = 1
x →0
lim
tg x
x →0
x
=1
Dapat dibuktikan berdasarkan (1) sbb :
tanx
sinx
lim
= lim
x →0
x →0 x(cosx)
x
sinx
1
. lim
= 1.1 = 1
x →0
x →0 (cosx)
x
= lim
Limit &
KALKULUS - 1
Slide - 7

8. 4)
x
x
lim tan x = 1
x →0
6) lim(1 + x ) 1 / x = e
x →0
5)
Bukti :
1
Misalkan x = y , berarti x → 0
maka y → ∝ sehingga :
lim(1+ x)
1/x
x →0
7) lim ln(1+ x) = 1
x →0
x
 1
lim 1 +  = e
x → ±∞
 x
Bukti :
1 y
= lim (1+ ) = e
y → ±∞
y
ln(1+ x)
= lim ln(1+ x)1/x
x →0
x →0
x
lim
= ln lim(1+ x)1/x = ln e = 1
x →0
Limit &
KALKULUS - 1
Slide - 8

9. Contoh :
tan3x
 tan3x  6x  1
= lim

.
x →0 tan6x
x →0
 3x  tan6x  2
1) lim
=
2)
1
tan3x
1
1
1
lim
.
= .1.1 =
2 3x →0 3x lim tan6x 2
2
6x →0
6x
 2
lim 1+ 
x →∞
 x
x
Misalkan x = 2y, maka y→ ∝ bila x →∝,
sehingga :
x

2 
 2
lim 1+  = lim 1+
 2y 

x →∞
 x  x →∞ 

3)
2y
2
  1 y 


=  lim 1+   = e 2
y →∞ 
y 
 
 

3
3
 1  x    1  x 
1

 


lim 1+  = lim 1+   =  lim 1+   = e3
x →∞
x →∞
 x
 x   x →∞ x  

 

Limit &
3x
KALKULUS - 1
Slide - 9

10. Beberapa macam metode untuk menentukan limit :
a) Menentukan limit dengan memfaktorkan :
Umumnya metode ini digunakan untuk menyelesaikan limit
aljabar pada fungsi pecahan :
Langkah-langkah yang digunakan adalah menyederhanakan
bentuk pecahan tersebut dengan memfaktorkan.
Contoh
x −1
lim x − 1
x →1
2
1)
=
=
x 2 + 5x + 6
(x + 2)(x + 3)
lim 2
= lim
2) x →2
x + 4x + 3 x →2 (x + 1)(x + 3)
(x + 1)(x − 1)
lim (x − 1)
x →1
(x + 2) 4
= lim
=
x →2 (x + 1)
3
lim(x + 1) = 2
x →1
Limit &
KALKULUS - 1
Slide - 10

11. b. Menentukan limit dengan merasionalkan bentuk akar :
Agar pecahan dapat disederhanakan pembilang dan
penyebut dikalikan dengan akar sekawannya.
Contoh :
2) lim
3 − 4x + 1
1) lim
x−2
x →2
x →1
x −1
x +3 −2
2
= lim
8 − 4x
(x − 2)(3 + 4x + 1)
= lim
− 4(x − 2)
(x − 2)(3 + 4x + 1)
= lim
−4
2
=−
3
3 + 4x + 1
x →2
x →2
Limit &
x →1
x2 + 3 + 2
x2 + 3 − 2 x2 + 3 + 2
(x − 1)( x 2 + 3 + 2)
= lim
x →1
(x 2 + 3) − 4
9 − (4x + 1)
= lim
x−2
x →2
x →2
= lim
(x − 1)
KALKULUS - 1
(x − 1)( x 2 + 3 + 2)
= lim
x →1
x2 − 1
(x − 1)( x 2 + 3 + 2)
= lim
x →1
(x − 1)(x + 1)
( x 2 + 3 + 2) 4
= lim
= =2
x →1
x +1
2
Slide - 11

12. c. Menentukan limit dengan membagi pembilang dan
penyebut dengan variabel pangkat tertinggi.
Metode ini digunakan untuk jenis fungsi pecahan dengan x mendekati tak
hingga (x → ∼), dilakukan dengan membagi pembilang dan penyebut dengan
variabel pangkat tertinggi.
1
lim x = 0
x →∞
Contoh :
x 3 − 4x 2 + 7
1) lim
2
3
x → ∞ 3 − 6x − 2x
x3
= lim
x →∞
=−
3
x
x
4x 2
3 −
6x
3 −
2
x
2)
x
3
+7
2x
3 −
3
x
2x 3
2x 3 x 3
lim 2
= lim 2 3
x →∞ x + 1
x →∞ x
x + 1 x3
3
x3
1
2
Limit &
KALKULUS - 1
2
x →∞ 1 x + 1 x 3
= lim
= ∞(tak ada limit)
Slide - 12

13. Limit Kiri dan Limit kanan
Jika x mendekati a dari kiri, maka x → aJika x mendekati a dari kanan, maka x → a+
Secara limit kedua pernyataan diatas ini ditulis sebagai berikut :
lim f(a) ada, berarti fungsi memiliki limit kiri
x →a −
lim f(a) ada, berarti fungsi memiliki limit kanan
x →a +
lim f(a) ada, mengandung arti bahwa keduanya limit kiri
x→a
Limit &
dan kanan ada dan sama.
KALKULUS - 1
Slide - 13

14. Contoh :
Selidiki :
1
lim
x → 0 3 + 21 / x
Jawab :
1
−
x → 0 , maka
2 1 / x →0.
Untuk :
→- ∝ dan
x
Maka :
1
1
1
lim
−
x →0
3+ 2
1/ x
=
3+0
=
3
1
1/ x
Untuk : x → 0 , maka x →+∝ dan 2
→∝.
+
Maka :
lim
+
x →0
1
1
= =0
3 + 21 / x ∞
Limit kiri ≠ limit kanan, sehingga
Limit &
1
lim
x → 0 3 + 21 / x
KALKULUS - 1
tidak ada.C
Slide - 14

15. Kontinuitas
Sebuah fungsi f(x) dikatakan kontinu di x = xo jika :
(i) f(xo) terdefinisi,
lim
(ii) x→ x f(x)
o
ada,
(iii) xlim f(x) = f(x o )
→x
Contoh :
o
f(x) = x2 + 1 kontinu di x = 2, karena lim f(x) = 5 = f(2)
:
x→ 2
Persyaratan ini mengandung arti bahwa fungsi hanya mungkin kontinu pada
titik dalam daerah definisinya.
Sebuah fungsi yg kontinu disetiap titik dlm suatu interval dikatakan kontinu
dlm interval tersebut, dan diskontinu pada x = xo jika satu atau lebih
syarat untuk kontinuitas tidak berlaku dititik tersebut.
Limit &
KALKULUS - 1
Slide - 15

16. Contoh diskontinuitas :
1) f ( x ) =
1
x−2
adalah diskontinu pada x = 2, karena :
(i) f(2) tidak terdefinisikan (mempunyai penyebut nol)
(ii) lim f ( x)
x→2
tidak ada (sama dengan ∞)
Fungsi ini kontinu dimana-mana kecuali pada x = 2 dimana
fungsi tsb dikatakan memp. diskontinuitas yg berhingga.
Limit &
KALKULUS - 1
Slide - 16

17. Contoh-contoh :
1) Hitunglah :
a) lim 5x = 5 lim x = 5.2 = 10
b ) lim(x 2 − 4x + 1) = 4 − 8 + 1 = −3
x − 2 lim(x − 2) 1
c) lim
= x →3
=
x →3 x + 2
lim(x + 2) 5
d) lim 25 − x 2 = lim(25 − x 2 )
x →2
x →2
x →3
x →2
x→4
x→4
= 9 =3
2) Hitunglah :
x−4
x−4
1
1
= lim
= lim
=
x → 4 x 2 − x − 12
x → 4 (x + 3)(x − 4)
x →4 x + 3
7
a) lim
Limit &
KALKULUS - 1
Slide - 17

18. x 3 − 27
(x − 3)(x 2 + 3x + 9)
x 2 + 3x + 9 9
= lim
= lim
=
b) lim 2
x →3 x − 9
x →3
x →3
(x − 3)(x + 3)
x+3
2
c)
d)
(4 − x 2 )(3 + x 2 + 5 )
= lim
x →2
4 − x2
x2 + x − 2
lim
x →1 (x − 1)2
(x − 1)(x + 2)
= lim
x →1
(x − 1)2
x+2
= lim
x→4 x − 1
= lim(3 + x 2 + 5 ) = 6
= ∞; tak ada limit
lim
x →2
4 − x2
3 − x2 + 5
= lim
x →2
4 − x2
(3 + x 2 + 5 )
3 − x 2 + 5 (3 + x 2 + 5 )
x →2
Limit &
KALKULUS - 1
Slide - 18

19. 3) Hitung :
3x − 2
3 − 2/x 3 − 0 1
= lim
=
=
x →∞ 9x + 7
x →∞ 9 + 7/x
9+0 3
a) lim
b)
c)
6x 2 + 2x + 1
6 − 2/x + 1/x 2 6 + 0 + 0
lim 2
= lim
=
=1
2
x →∞ 6x − 3x + 4
x →∞ 6 − 3/x + 1/x
6−0−0
4x 3
4
lim
= lim
= ∞ (tidak ada limit)
x →∞ x 2 + 5
x →∞ 1/x + 5/x 2
Limit &
KALKULUS - 1
Slide - 19

20. Soal-soal :
1) Selesaikan :
a) lim(x 2 − 4x)
x→2
b) lim
x →1
1/3
 4y + 8y 

f) lim

y →2
 y+4 
3
u2 − 2u + 1
g) lim
u→ 2
u2 + 4
x −1
x2 + 3 − 2
c) lim (x 3 + 2x 2 − 3x − 4)
(3x − 1)2
h) lim
x → −1 (x + 1)3
x 2 + 3x + 2
d) lim 2
x → −1 x + 4x + 3
(y − 1)(y 2 + 2y − 3)
i) lim
y →1
y 2 − 2y + 1
(w + 2)(w 2 − w − 6)
e) lim
w →−2
w 2 + 4w + 4
j) lim (2w 4 − 9w 3 + 19) −1/2
x → −1
Limit &
KALKULUS - 1
w →5
Slide - 20

21. 3) Hitung :
sin(4x)
e) lim
x→0 2sinxcosx
1− cosx
x →0
x
a) lim
sin2 (x/4)
f) lim
x →0
x2
tan(3x)
b) lim
x→0 sin(2x)
sin(2x) − 2sinx
c) lim
x →0
sin(3x)
g) lim
x 2
d) lim
x →0 1 − cosx
h) lim
Limit &
sin(x + a) + sin(x − a)
x →0
x
5sin(x + 1)
x →0 tan(x + 1)
KALKULUS - 1
Slide - 21

22. 4) Tentukan :
a) lim [ln(9x + 1) − ln(3x + 1)]
x→ ∞
6) Tentukan titik2 diskontinu
& jenis diskontinuitas
dari fungsi-fungsi :
b) lim {ln(x + 4x − 5) − ln(x − 1)}
2
x →∞
 1
c) lim 1+ 
n→ ∞
 n
n+ 5
 5x − 1 
d) lim 

x →∞ 5x + 1


 n + 10 
e) lim 

n→ ∞ n + 5


x −1
b) f(x) = 2
x −1
4x
c) f(x) =
3n −1
1 

f) lim 1+

n→∞
 n+3
Limit &
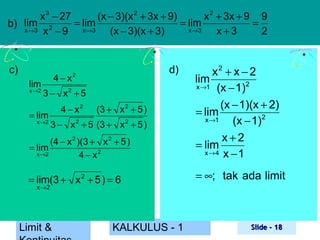
x 3 − 27
a) f(x) = 3
x −9
4 − x2
3 − x2 + 5
x 4 − 16
d) f(x) = 2
x −4
5n −1
KALKULUS - 1
Slide - 22