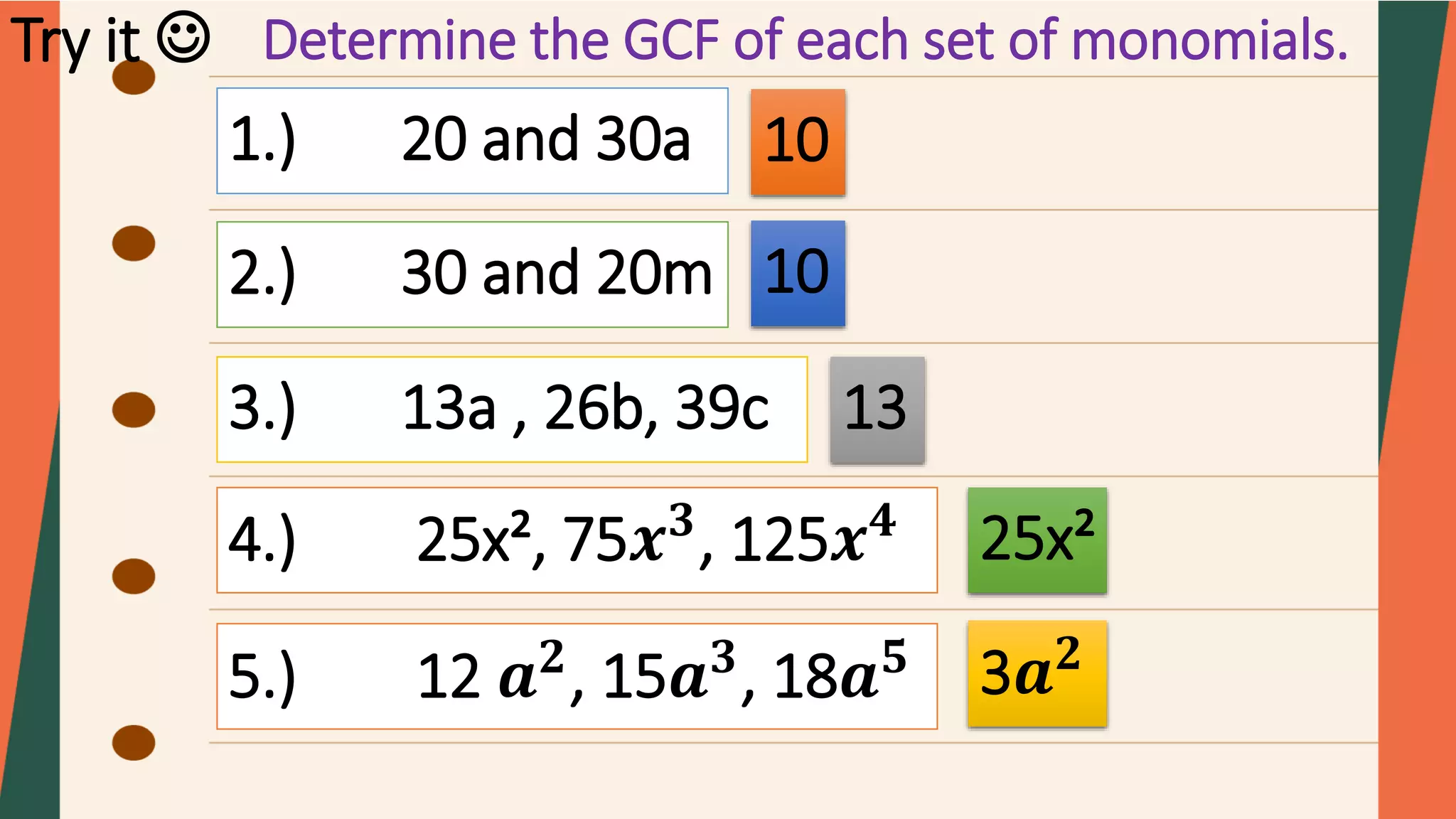
This document contains a lesson on factoring polynomials. It begins with examples of factoring various polynomials and identifying the greatest common factor. It then discusses key terminology related to factoring like common monomial factor and factor. The document provides step-by-step worked examples of factoring polynomials. It concludes with a generalization section and seat work problems for students to practice factoring polynomials.

1. Good Afternoon
Grade 8

2. Answers:
Learning Task 1:
1. C
2. A
3. D
4. B
5. E
Learning Task 2:
1. (x+6)(x-3)
2. (3x+3)(x-4)
3. (18x-15)(x+1)
4. (5x+2)(x+6)
5. 3(x+2)(x²-2x+4)
Learning Task 3:
1. x=0, x=8
2. x=0,x=10
3. x=3, x= -9

3. Review Time 
3(4)
12

4. Review Time 
-2(10)
-20

5. Review Time 
-2(-7)
14

6. Review Time 
3(-9)
-27

7. Review Time 
x(x)
𝒙𝟐

8. Review Time 
x(x)(x)
𝒙𝟑

9. Review Time 
x(x)(x)(y)
𝒙𝟑
𝒚

10. Review Time 
2x(3𝒙𝟐
)
𝟔𝒙𝟑

11. Review Time 
-6m(3𝒏𝟐
)
−𝟏𝟖𝒎𝒏𝟐

12. Review Time 
-7y(-7y)
𝟒𝟗𝒚𝟐

13. Review Time 
What are the factors of 4?
1 · 4 2 · 2
𝑇ℎ𝑒 𝑓𝑎𝑐𝑡𝑜𝑟𝑠 𝑜𝑓 4 𝑎𝑟𝑒 1, 2 & 4.

14. Review Time 
What are the factors of 8?
1 · 8 2 · 4
𝑇ℎ𝑒 𝑓𝑎𝑐𝑡𝑜𝑟𝑠 𝑜𝑓 8 𝑎𝑟𝑒 1, 2, 4 & 8.

15. Review Time 
What are the factors of 2?
1 · 2
𝑇ℎ𝑒 𝑓𝑎𝑐𝑡𝑜𝑟𝑠 𝑜𝑓 2 𝑎𝑟𝑒 1 & 2.

16. Review Time 
What are the factors of -2?
-1 · 2 1 · -2
𝑇ℎ𝑒 𝑓𝑎𝑐𝑡𝑜𝑟𝑠 𝑜𝑓 − 2 𝑎𝑟𝑒 1, −1, 2 & − 2.

17. Review Time 
What are the factors of -9?
-1 · 9 1 · -9
𝑇ℎ𝑒 𝑓𝑎𝑐𝑡𝑜𝑟𝑠 𝑜𝑓 − 9 𝑎𝑟𝑒 1, −1, 3, −3,
9 & − 9.
3 · -3

18. Review Time 
What are the factors of 𝒙𝟑
?
x · x · x

19. Review Time 
What are the factors of 𝒎𝟐
?
m · m

20. Finding the products Finding the factors
x · x = x² x² = (x)(x)
y · y = y² y² = (y)(y)
3 · 4 = 12 12 = (3)(4)
3x · 4x = 12x² 12x² = (2)(2)(3)(x)(x)
3xy · 4xy = 12x²y² 12x²y² = (2)(2)(3)(x)(x)(y)(y)
What is your observation from the given examples?

21. Did you remember what is GCF?
Greatest Common Factor
4 6
1 4
2 2
1 6
2 3
1, 2, 4 1, 2, 3, 6
2

22. Did you remember what is CMF?
Common Monomial Factor
x² 2x²
1 1
x x
1 2
x x
1 and x² 1, 2 and x²
x²

23. Polynomial CMF Factored Form
x² + 2x x x(x + 2)
4x² + 6x 2x 2x(2x + 3)
3x² + 6x 3x 3x(x + 2)
5x² + 10x³ 5x² 5x²(1 + 2x)
6x⁴ - 14x² 2x² 2x²(3x² - 7)

24. Factoring is finding two or more factors of a
number or a polynomial.
The Greatest Common Factor (GCF) of two or
more monomials is the common factor having
the greatest numerical factor and with
variables having the least degree. Thus, the
term 𝒂𝒙𝒏
is the GCF of a polynomial if;
1. a is the greatest integer that divides each
of the coefficients of the polynomials, and
2. n is the smallest exponents of x in all terms
of the polynomial

25. Terminologies:
CMF – Common Monomial Factor (the
factor contained in every term)
Factor – an exact divisor of a number
Monomial – a mathematical expression
containing one term

26. Example 1:
Find the Greatest Factor of each pair of
monomials.
A.) 12a and 36ab
B.) 6a and 20a²b
C.) – 8x²y and 16xy
12a
2a
-8xy

27. Example 2:
Factor completely.
A.) 5x + 10
B.) . 25x²𝒚𝟑
– 55x𝒚𝟑
C.) 12a²𝒃𝟒 - 16𝒂𝟑𝒃𝟐 + 20𝒂𝟓𝒃𝟑
5(x + 2)
5xy³(5x – 11)
4a²b²(3b² - 4a +5a³b)

28. Example 3:
A.) 5a(a + 3) – c(a + 3)
B.) 6(3b – 1) + 5a(1 – 3b) + 4c(3b – 1)
(a + 3)(5a – c)
(3b – 1)(6 – 5a + 4c)

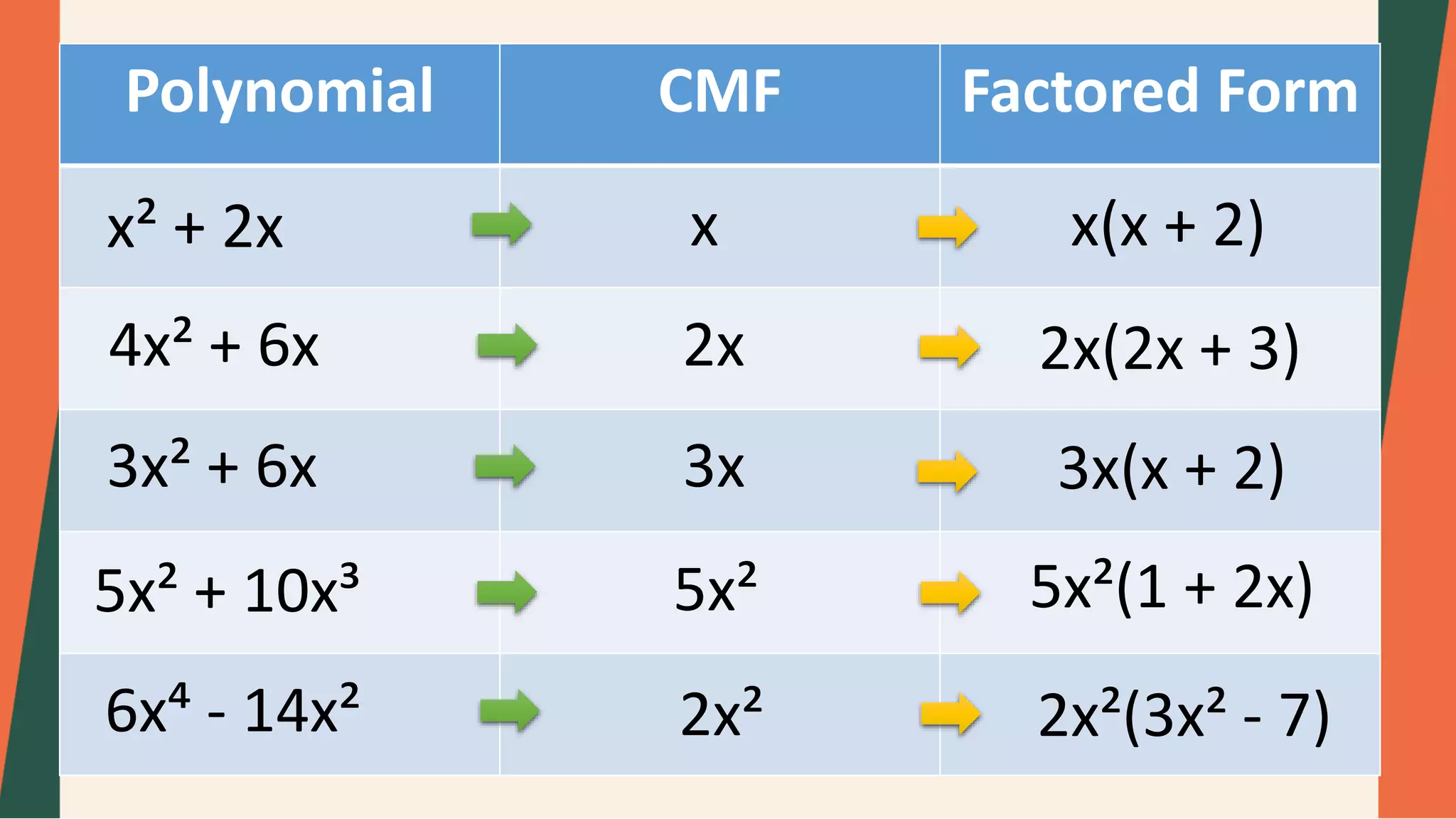
29. Example 3:
D.) 6x²(y + 2)² + 12x(𝒚 + 𝟐)𝟒
6x(y + 2)²[x + 2(y + 2)²]
C.) 𝐩𝟑 𝐧 + 𝟐 + 𝟐𝐩𝟐 𝐧 + 𝟐 − 𝟓𝐩(𝐧 + 𝟐)
p(n + 2)(p² + 2p – 5)

30. Try it  Determine the GCF of each set of monomials.
1.) 20 and 30a 10
2.) 30 and 20m
3.) 13a , 26b, 39c
4.) 25x², 75𝒙𝟑
, 125𝒙𝟒
10
13
25x²
5.) 12 𝒂𝟐
, 15𝒂𝟑
, 18𝒂𝟓 3𝒂𝟐

31. Try it 
Write a polynomial in each to complete
each statement.
A.) 7p² - 7p = 7p( )
B.) 6a²b + 24𝒂𝟑
= 6a²( )
p – 1
b + 4a

32. The formula for the perimeter of a
rectangle is given by P = 21 + 2w, where 1
represents the length and w represents the
width. Use Factoring to rewrite the
formula.
Practical Application
The GCF of the terms is 2.
P = 2l + 2w
P = 2(l + w)

33. A. Fill in the each blank to make a true statement.
Generalization
1. After multiplying, we have a(b + c) = ________.
2. By factoring, we have ab + ac = ___________.
3. The term 4𝒙𝟑
is the GCF of a polynomial if
______ is the greatest integer that divides each
of the coefficient of the polynomial and _____ is
the smallest exponent of x in all terms of the
polynomial.
ab + ac
a(b + c)
4
3

34. Generalization
B. What is factoring?
C. What is CMF?
Common Monomial Factor
Factoring is finding two or more factors
of a number or a polynomial.

35. Seat Work:
POLYNOMIAL CMF FACTORED
FORM
1.) 25 + 45x
2.) 24a + 48b
3.) x2 + 2x
4.) 5x2 – 10x3
5.) 25x2y3 + 55xy3
5 5(5 + 9x)
8 8(3a + 6b)
x x(x + 2)
5x² 5x²(1 – 2x)
5xy³ 5xy³(5x + 11)