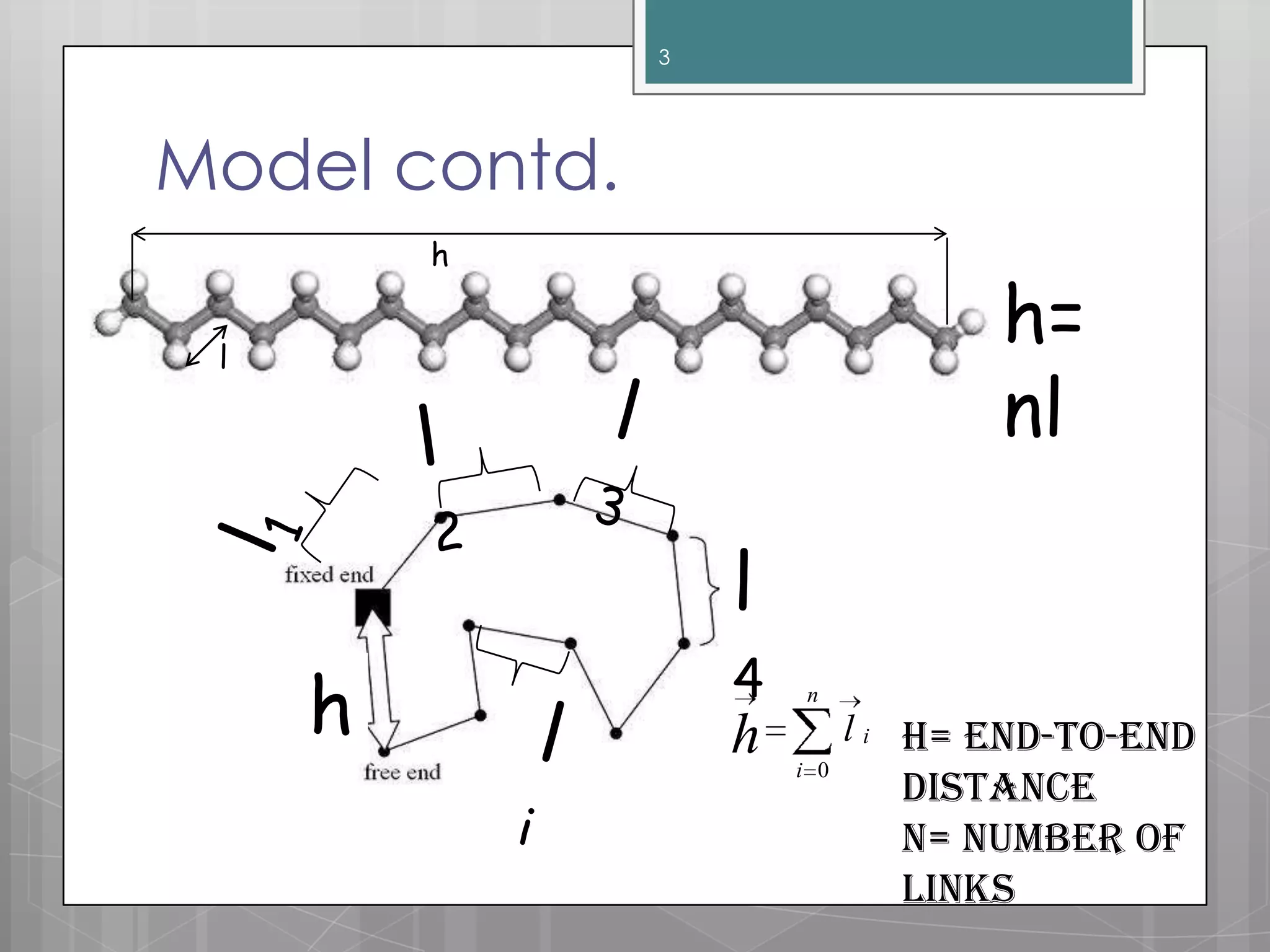
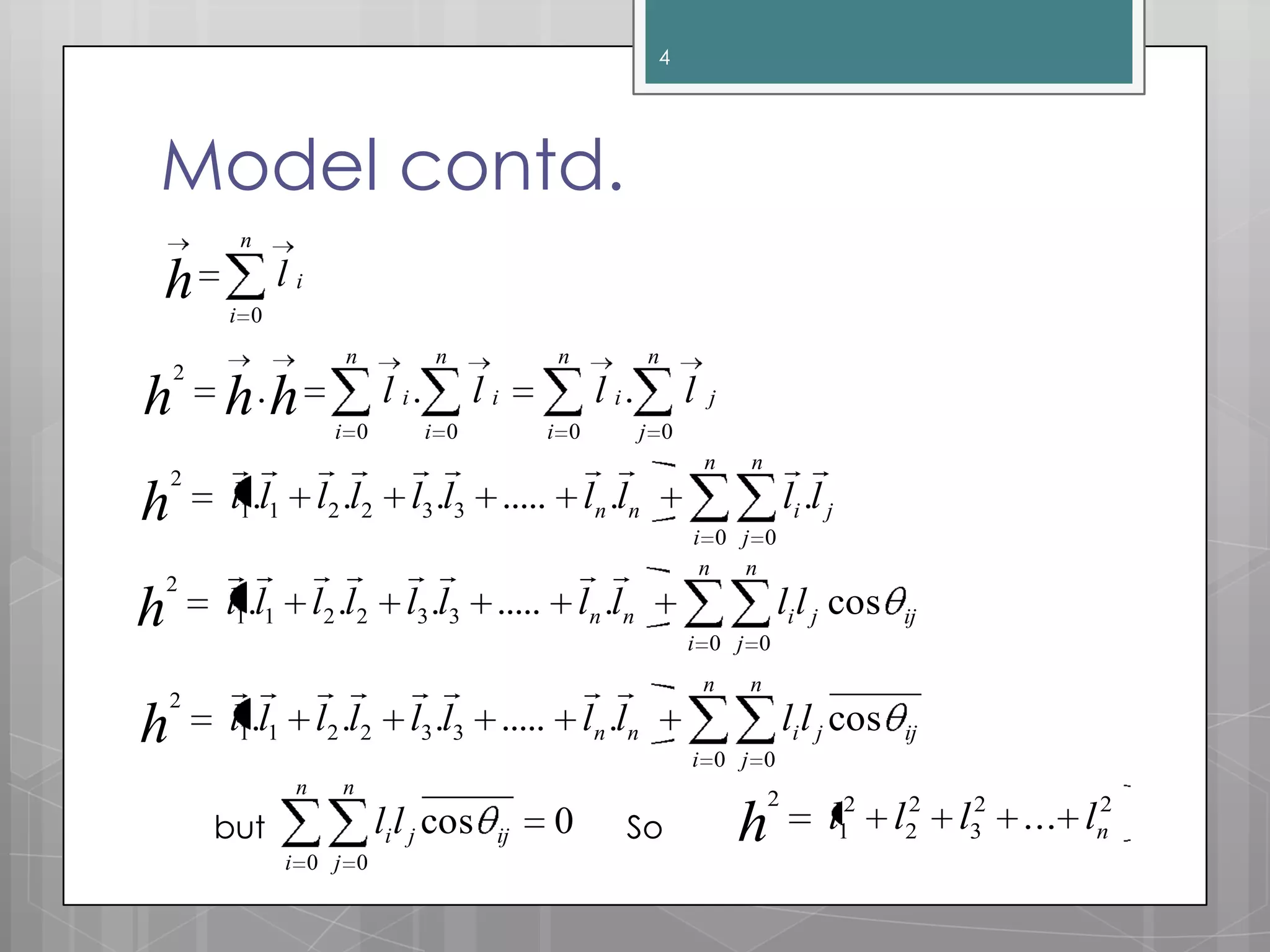
The document discusses polymer chain dimensions using the freely jointed chain model and Gaussian distribution function. It describes the freely jointed chain model, which assumes no restrictions on bond angles, rotations, or van der Waals volume. The model shows that the root mean square end-to-end distance of an ideal chain is proportional to the square root of the number of links. It then introduces the Gaussian distribution function and shows that it gives the same results as the freely jointed chain model for the average end-to-end distance. The document finally notes some corrections needed for real chains, which include restrictions due to bond angles, steric hindrance from bulky groups, and excluded volume effects.

1. Polymer
Conformation
& Chain
Dimension
Aman Pratap Singh Rajvi
2010B2AB716P1

2. Model: Freely Jointed Model or
Random Flight Model
 Assumptions:
 No restrictions of – Valence Angle, Rotation &
Vander-waals’ Volume
 Short range correlations between
neighboring monomers are not excluded.
 Ideal chain models do not take interactions
caused by conformations in space into
account.
 Ideal chains allow the polymer to cross itself.
 Fully idealized hypothetical model.
2

3. Model contd.
3
l
h
h=
nl
l
4
h n
i
ilh 0
h= end-to-end
distance
n= number of
links

4. Model contd.
4
n
i
ilh 0
n
j
j
n
i
i
n
i
i
n
i
i llllhhh 0000
2
...
n
i
n
j
jinn llllllllllh 0 0
332211
2
..........

n
i
n
j
ijjinn llllllllllh 0 0
332211
2
cos.........

n
i
n
j
ijjinn llllllllllh 0 0
332211
2
cos.........

n
i
n
j
ijjill
0 0
0cosbut So
22
3
2
2
2
1
2
... nllllh

5. Model contd.
 Mean square bond length:

 If all bonds are of same length, i.e., l
 Root Mean Square (RMS) end-to-end distance=
=
5
n
llll
l n
av
22
3
2
2
2
12 ...
n
h
lav
2
2

22
avnlh

2
22222
2
...
l
n
nl
n
llll
lav
nlnl2

6. Using Gaussian Distribution
Function
 n= no. of segments
 l= length of each link
 Gaussian Distribution
Function=
6
),,(
22
3
2
1
zyxwe
b rb
r
dy
dx
dz

7. Gaussian Distribution Function
contd.
 Taking spherical coordinates
7
dr
r
ddre
b
drw rb 22
3
2
1
sin),,(
22
2
3
2
1
4)(
22
re
b
rw rb
r=radius of
spherical shell
b=3/2nl2

8. Gaussian Distribution Function
contd.
 Which is same as what we got from Freely
Jointed Chain Model
8
2
0
0
2
2
)(
)(
nl
drrw
drrwr
r RMS end-to-end Distance nl

9. Considering Real Chain
 Restriction due to valance bond angle
9
cos1
cos122
nlr

10. Real Chain contd.
 Restrictions because of Steric Hindrance
as a result of presence of bulky group
10
cos1
cos1
cos1
cos122
nlr Dihedral angle

11. Real Chain contd.
 Correction due to excluded volume
11
lnCr N
2
1
2
)(
Expansion factor which is a
measure of excluded volume
2
2
0
nl
r
0: Excluded volume
1: No excluded volume
22222
.)( nlClnCr NN
2
2
0
nl
r
CN
Unperturbed Mean square
end-to-end distance
Mean square end-to-end
distance

12. Thank You
12