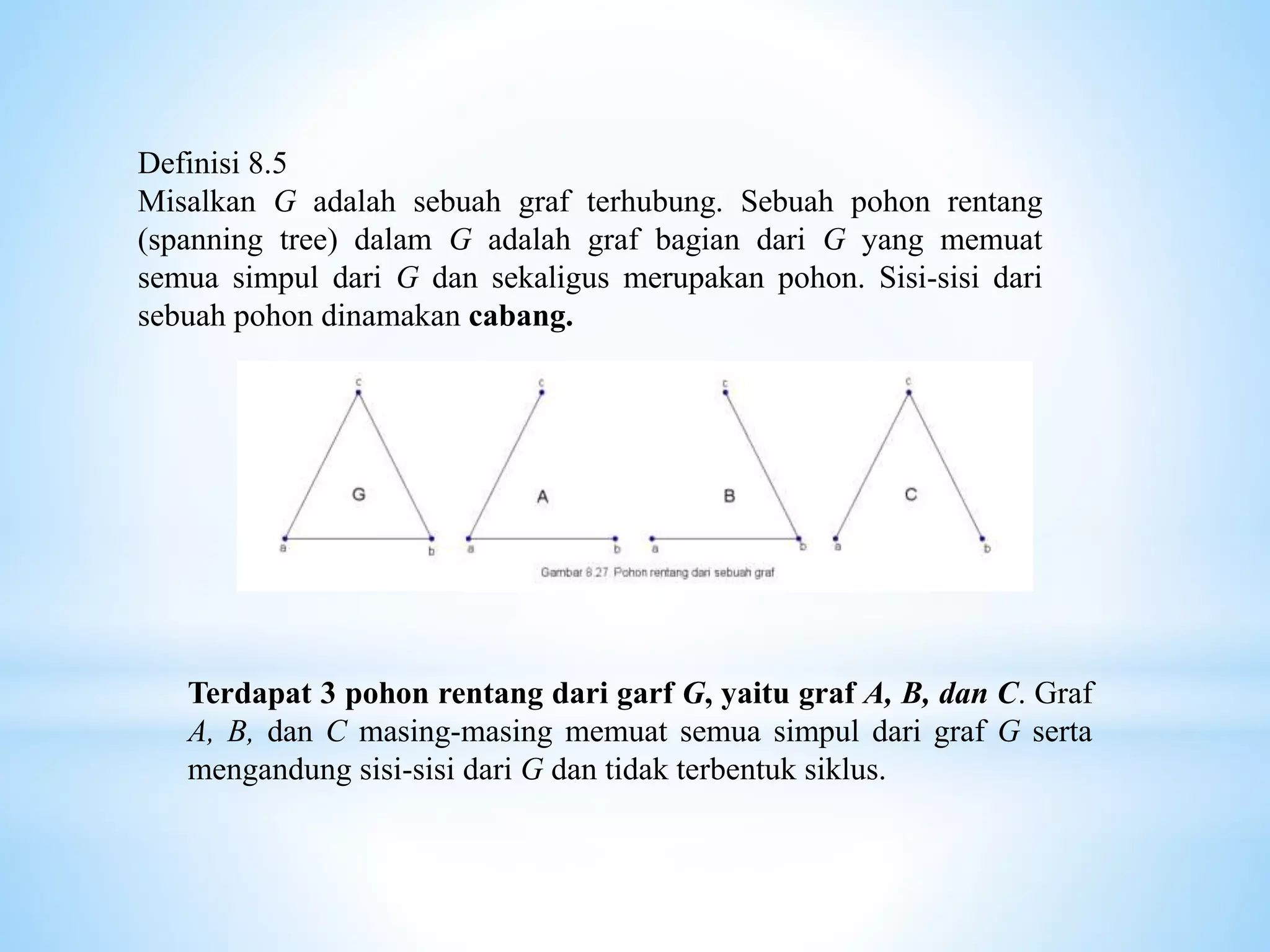
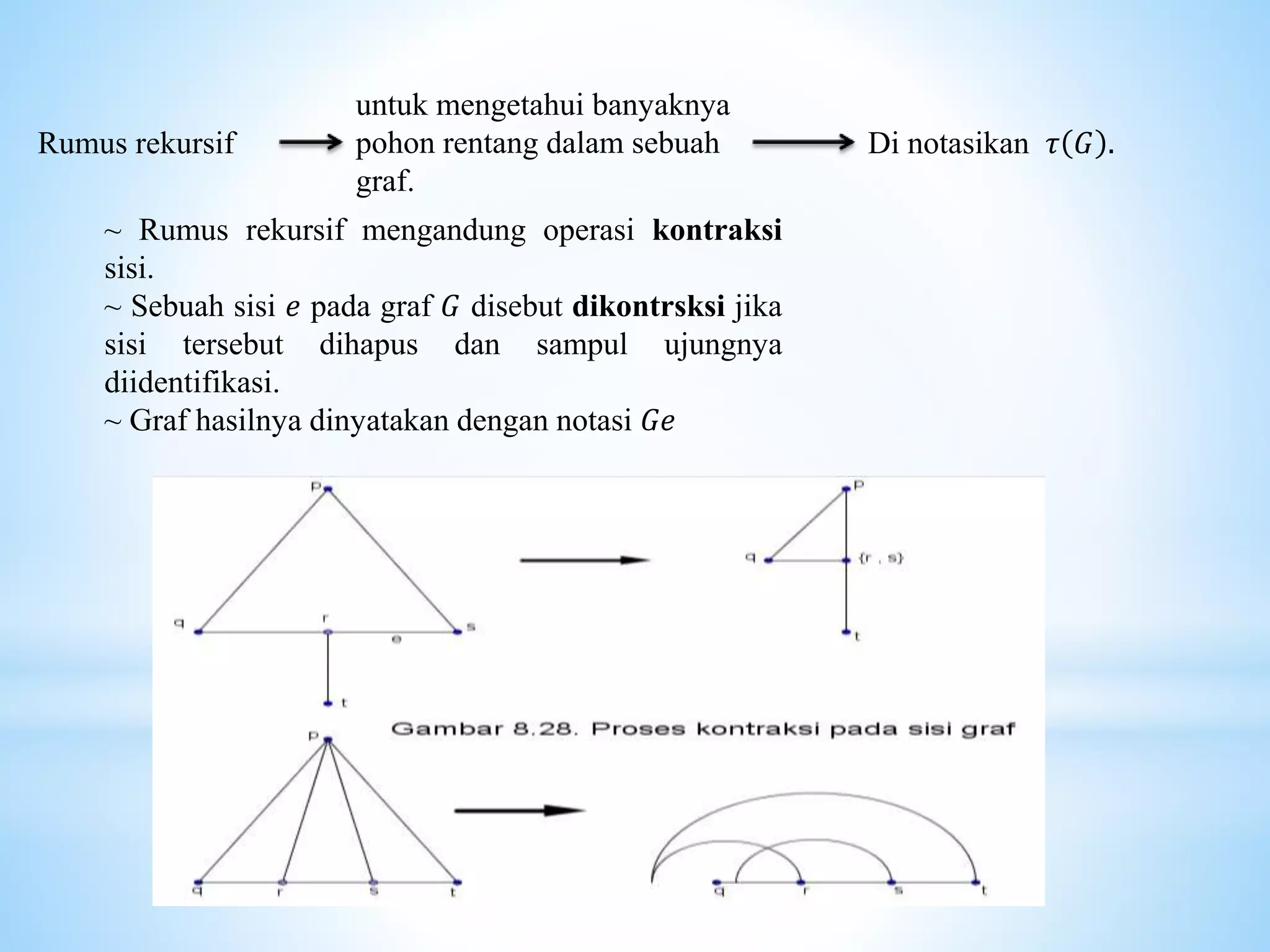
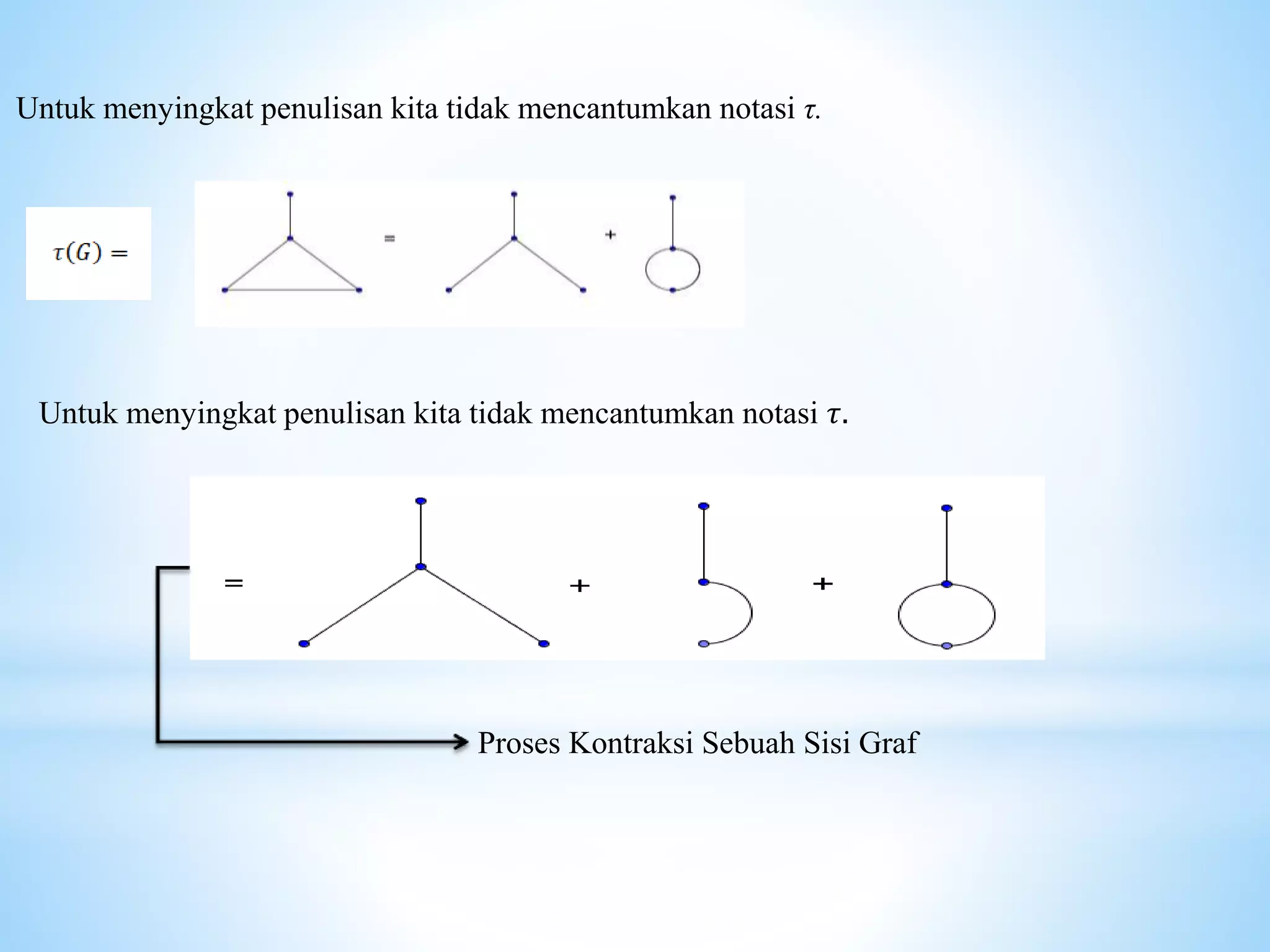
Dokumen ini membahas konsep pohon rentang dalam teori graf, menjelaskan definisi, sifat-sifat, dan teorema yang mendasari keberadaan pohon rentang dalam graf terhubung. Selain itu, juga dijelaskan tentang proses kontraksi sisi dan rumus untuk menghitung jumlah pohon rentang dalam graf lengkap. Teorema-teorema yang disajikan memberikan bukti keterhubungan antara simpul dalam graf dan eksistensi pohon rentang.

1. POHON RENTANG
Kelompok 3 :
~ Endah Nisa Fauziah
~ Nurhayati
~ Sari Agustina
Matkul : Matematika Diskrit
Dosen : Nia Kania, M. Pd.

2. F merupakan graf bagian dari G,
karena graf G memuat semua simpul
dan sisi yang ada pada graf F.
Maka :
Graf F merupakan pohon, dan
dinamakan pohon rentang
(spanning tree).
POHON RENTANG
Hutan rentang merupakan bagian dari sebuah graf tak
terhubung, dan tiap-tiap komponennya merupakan
pohon.

3. Definisi 8.5
Misalkan G adalah sebuah graf terhubung. Sebuah pohon rentang
(spanning tree) dalam G adalah graf bagian dari G yang memuat
semua simpul dari G dan sekaligus merupakan pohon. Sisi-sisi dari
sebuah pohon dinamakan cabang.
Terdapat 3 pohon rentang dari garf G, yaitu graf A, B, dan C. Graf
A, B, dan C masing-masing memuat semua simpul dari graf G serta
mengandung sisi-sisi dari G dan tidak terbentuk siklus.

4. Teorema 8.6
Misalkan 𝐺 = (𝑉, 𝐸) merupakan sebuah graf sederhana. G terhubung jika dan
hanya jika G mempunyai sebuah pohon rentang.
Bukti :
Jika 𝐺 mempunyai sebuah pohon rentang 𝑇, maka untuk setiap pasangan simpul
𝑢, 𝑣 yang berlainan dalam 𝑉 sebuah himpunan bagian dari himpunan sisi pada 𝑇
memberikan sebuah lintasan yang unik antara 𝑢 dan 𝑣, dan dengan demikian 𝐺
merupakan graf terhubung. Sebaliknya, jika 𝐺 merupakan graf terhubung dan 𝐺
bukanlah sebuah pohon, maka hapuslah semua loop dari 𝑔. Jika graf bagian yang
dihasilkan 𝐺1 tidak merupakan sebuah pohon, maka 𝐺1 harus memuat sebuah
siklus. Hapuslah sebuah sisi, misalnya 𝑒1, dari 𝐺1 dan misalkan 𝐺2 = 𝐺1 − 𝑒1. Jika
𝐺2 tak memuat siklus, maka 𝐺2 merupakan pohon rentang bagi graf 𝐺 karena 𝐺2
memuat semua simpul dalam 𝐺, bebas dari loop, dan terhubung. Jika 𝐺2 memuat
sebuah siklus, misalnya kita namakan 𝐺2, maka hapuslah sebuah sisi 𝑒2 dari 𝐺2 dan
perhatikan graf bagian 𝐺3 = 𝐺2 − 𝑒2 = 𝐺1 − {𝑒1−𝑒2}. Berikutnya, jika 𝐺3 tak
memuat siklus, maka kita mempunyai pohon rentang bagi 𝐺. Kalau tidak demikian
halnya, kita teruskan prosedur ini dalam terhingga iterasi, yang akan mengantar
kita pada graf bagian rentang dari 𝐺 yang tanpa loop, terhubung dan tanpa siklus,
yang sekaligus mengisyaratkan bahwa graf bagian tersebut merupakan graf rentang
bagi 𝐺.

5. Teorema 8.7
Misalkan 𝑇 adalah sebuah pohon rentang dari graf terhubung 𝐺 dan
misalkan 𝑒 sebagai sisi dari 𝐺 yang tidak pada 𝑇 . Maka 𝑇 + 𝑒
mengandung sebuah siklus unik.
Bukti :
Karena 𝑇 tidak memuat siklus, tiap siklus dari 𝑇 + 𝑒 memuat 𝑒. Selain itu,
𝐺 merupakan sebuah siklus dari 𝑇 + 𝑒 jika dan hanya jika 𝐺𝑒 merupakan
sebuah lintasan dalam 𝑇 yang menghubungkan simpul ujung dari 𝑒.
Berdasarkan Teorema sebelumnya, yang menyatakan bahwa tiap dua
simpul dalam sebuah pohon dihubungkan dengan sebuah lintasan yang
unik, maka 𝑇 + 𝑒 memuat siklus yang unik.

6. ~ Rumus rekursif mengandung operasi kontraksi
sisi.
~ Sebuah sisi 𝑒 pada graf 𝐺 disebut dikontrsksi jika
sisi tersebut dihapus dan sampul ujungnya
diidentifikasi.
~ Graf hasilnya dinyatakan dengan notasi 𝐺𝑒
Rumus rekursif
untuk mengetahui banyaknya
pohon rentang dalam sebuah
graf.
Di notasikan 𝜏 𝐺 .

7. Teorema 8.8
Jika 𝑒 merupakan sebuah pengait dari 𝐺, maka 𝜏 𝐺 = 𝜏 𝐺 − 𝑒 +
𝜏 𝐺. 𝑒
Bukti :
Pohon rentang dari sebuah graf 𝐺 yang tidak mengandung sisi 𝑒 adalah juga
sebuah rentang dari 𝐺𝑒, dan sebaliknya, maka 𝜏(𝐺. 𝑒) merupakan banyaknya
pohon rentang dari 𝐺 yang tidak mengandung sisi 𝑒.
Tentukan banyaknya pohon rentang dari graf berikut :
Contoh :

8. Untuk menyingkat penulisan kita tidak mencantumkan notasi τ.
Untuk menyingkat penulisan kita tidak mencantumkan notasi 𝜏.
Proses Kontraksi Sebuah Sisi Graf

9. Teorema 8.9
Misalkan 𝑛 menyatakan banyaknya simpul pada graf lengkap 𝐾 𝑛. Maka berlaku
𝜏(𝐾 𝑛) = 𝑛 𝑛−2.
Bukti :
Misalkan simpul dari graf 𝐾 𝑛 adalah 1, 2, 3, … , 𝑛. Kita tahu bahwa 𝑛 𝑛−2 adalah
banyaknya barisan dengan panjang 𝑛 − 2 yang dapat dibentuk dari simpul-simpul
1, 2, 3, … , 𝑛. Dengan demikian untuk membuktikan teorema ini kita cukup
menciptakan korespondensi satu-satu antara pohon rentang-pohon rentang dari 𝐾 𝑛
dan barisan tersebut.

10. Terimakasih 