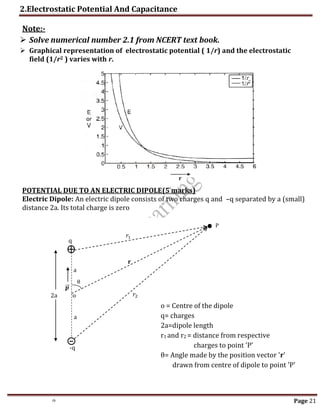
1. The document discusses electrostatic potential and capacitance. It defines electrostatic potential energy as the work done by an external force in bringing a charge from infinity to a point in an electric field. 2. The potential due to a point charge is directly proportional to the charge and inversely proportional to the distance from the point charge. The potential due to an electric dipole depends on the cosine of the angle between the position vector and the dipole axis. 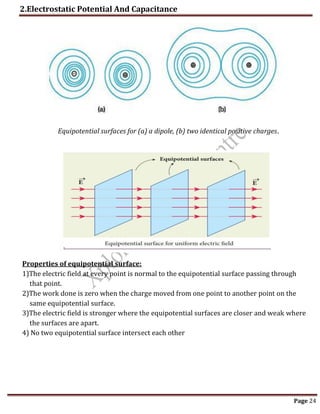3. Equipotential surfaces represent points in space with the same electric potential. Electric field lines are perpendicular to equipotential surfaces. Potential decreases in the direction of increasing electric field strength.

1. 2.Electrostatic Potential And Capacitance
th Page 18
INTRODUCTION
POTENTIAL ENERGY:-
When an external force does work in taking a body from a point to another against a
force like spring force or gravitational force, that work stored in the form of potential
energy of the body.
Gravitational Field:- The space around an mass where another mass experience a force of
attraction .The work done stored in this field is called as Gravitational Potential energy.
The gravitational P.E. depends on the height of a mass above the earth surface.
Electric Field:- The space around an charge where another charge experience a force of
attraction/repulsion .The work done stored in this field is called as Electrical Potential
energy.
The electrical P.E. depends on the position of charged particle in the electric field.
ELECTRICAL POTENTIAL ENERGY:-
Potential energy of charge q at a point (in the presence of field due to any charge
configuration) is the work done by the external force in bringing the charge q from infinity
to that point.
The external force is equal and opposite to the electric force (i.e, Fext= –FE).
Explaination:
Consider the field E due to a charge Q placed at the origin. Now, imagine that we
bring a test charge q from a point R to a point P against the repulsive force on it due to the
charge Q as shown in figure.(where Q, q > 0). Bringing the charge q from R to P, we apply an
external force Fext just enough to counter the repulsive electric force FE (i.e, Fext= –FE).
`
If the external force is removed on reaching P, the electric force will take the charge
away from Q this happen due to stored energy (potential energy) at P is used to provide
kinetic energy to the charge q .Thus, work done by external forces in moving a charge
q from R to P is,
P
R
q
Q

2. 2.Electrostatic Potential And Capacitance
Page 19
𝑊𝑅𝑃 = ∫ 𝐹𝑒𝑥𝑡
𝑃
𝑅
∙ 𝒅𝒓
𝑊𝑅𝑃 = − ∫ 𝐹𝐸
𝑃
𝑅
∙ 𝒅𝒓
This work done is against electrostatic repulsive force and gets stored as potential energy.
 Some important feature of electric potential energy are:
1. It is a scalar quantity measured in Joule.
2. The work done by an electrostatic field in moving a charge from one point to another
depends only on the initial and the final points and is independent of the path taken
to go from one point to the other.
3. Electric potential energy difference between two points as the work required to be
done by an external force in moving (without accelerating) charge q from one point
to another for electric field of any arbitrary charge configuration.
i.e ∇𝑈 = 𝑈𝑃 − 𝑈𝑅 = 𝑊𝑅𝑃
ELECTROSTATIC POTENTIAL(V):
Work done by an external force in bringing a unit positive charge from infinity to a
point is called as electrostatic potential (V ) at that point.
𝑽 =
𝑾
𝒒
NOTE: 1) Electric potential is scalar quantity.
2)Unit is Volt(V)
POTENTIAL DUE TO A POINT CHARGE:(5marks)
Consider a positive point charge 'Q' placed at origin. Let a point 'P' is located at
distance r from the origin where electrical potential is to be calculated. To do this we must
bring a unit positive test charge (+1C) from infinity to that point .
P
r
dx
O
Q
A
B
x
∞
+1C

3. 2.Electrostatic Potential And Capacitance
Page 20
r
∞
Consider any arbitrary points A and B separated by small distance 'dx'. When a unit
positive charge brought at 'A' from infinity then repulsive force on positive test charge is
given by Coulombs law,
𝐹 =
𝑄×1
4𝜋𝜀0𝑥2-------------------------------(1)
The work done in moving a unit positive charge from A to B through a small displacement
is given by
dw = Force x Displacement
𝑑𝑤 = −𝐹 × 𝑑𝑥
𝑑𝑤 = −
𝑄
4𝜋𝜀0𝑥2 × 𝑑𝑥
work done (W) by the external force is obtained by integrating the above equation between
the limit x=∞ and x=r
𝑊 = − ∫
𝑄
4𝜋𝜀0𝑥2 × 𝑑𝑥
𝑟
∞
=
𝑄
4𝜋𝜀0𝑥
|
𝑊 =
𝑄
4𝜋𝜀0
[
1
𝑟
−
1
∞
]
𝑊 =
𝑄
4𝜋𝜀0𝑟
From definition of electrostatic potential at point P is
𝑉 =
𝑊
𝑞
but q=1C
𝐕 =
𝐐
𝟒𝛑𝛆𝟎𝐫
Define 1 volt potential(Define unit of potential)
The potential difference between two points is said to be 1 volt if 1 joule of work is done in
moving a positive charge of 1 coulomb from one point to the other against the electrostatic
force.

4. 2.Electrostatic Potential And Capacitance
th Page 21
r
Note:-
 Solve numerical number 2.1 from NCERT text book.
 Graphical representation of electrostatic potential ( 1/r) and the electrostatic
field (1/r2 ) varies with r.
POTENTIAL DUE TO AN ELECTRIC DIPOLE(5 marks)
Electric Dipole: An electric dipole consists of two charges q and –q separated by a (small)
distance 2a. Its total charge is zero
2a
q
-q
θ
a
a
o
𝑟1
𝑟2
r
𝒑
⃗
⃗
o = Centre of the dipole
q= charges
2a=dipole length
r1 and r2 = distance from respective
charges to point 'P'
θ= Angle made by the position vector 'r'
drawn from centre of dipole to point 'P'
P

5. 2.Electrostatic Potential And Capacitance
Page 22
As we know that the electrical potential is scalar quantity. Hence the total potential at point
'P' due to dipole is the sum of the potential due to +q charge and -q charge respectively.
V+q =
q
4πε0r1
and V−q = −
q
4πε0r2
V = V+q + V−q
V =
q
4πε0r1
−
q
4πε0r2
V =
q
4πε0
[
1
r1
−
1
r2
]
V =
q
4πε0
[
r2 − r1
r1r2
]
but for ' r ≪ a ' then from diagram r1 = r2 = r and r2 − r1 = 2a cos θ
V =
q
4πε0
[
2a cosθ
r2 ] but P=2qa (dipole moment)
𝐕 =
𝐏 𝐜𝐨𝐬𝛉
𝟒𝛑𝛆𝟎𝐫𝟐
Note:1) Potential on the dipole axis(θ=0o or 180o).------------------- V = ±
P
4πε0r2 (1 mark)
2) The potential in the equatorial plane (θ=90o ) is zero.----- V= 0 (1 mark)
3) Total charge on the dipole is ZERO.(1 marks)
th

6. 2.Electrostatic Potential And Capacitance
Page 23
POTENTIAL DUE TO A SYSTEM OF CHARGES
V = V1 + V2 + V3 + V4 + V5 … … . Vn
V =
q1
4πε0r1P
+
q1
4πε0r2P
+
q1
4πε0r3P
+
q1
4πε0r4P
+
q1
4πε0r5P
…… ….
qn
4πε0rnP
𝐕 =
𝟏
𝟒𝛑𝛆𝟎
[
𝐪𝟏
𝐫𝟏𝐏
+
𝐪𝟐
𝐫𝟐𝐏
+
𝐪𝟑
𝐫𝟑𝐏
+
𝐪𝟒
𝐫𝟒𝐏
+
𝐪𝟓
𝐫𝟓𝐏
…….
𝐪𝐧
𝐫𝐧𝐏
]
 Assignment: Solve numerical number 2.2 and 2.3 from NCERT text book.
EQUIPOTENTIAL SURFACES:-
An equipotential surface is a surface with a constant value of potential at all points on
the surface.
𝑞1 𝑞5
𝑞4
𝑞3
𝑞2
P
Consider five charges
placed at their
respective positions
as shown in figure.
The potential at point
P due to all charges is
the algebric sum of
potential due to each
charges at that point.

7. 2.Electrostatic Potential And Capacitance
Page 24
Equipotential surfaces for (a) a dipole, (b) two identical positive charges.
Properties of equipotential surface:
1)The electric field at every point is normal to the equipotential surface passing through
that point.
2)The work done is zero when the charge moved from one point to another point on the
same equipotential surface.
3)The electric field is stronger where the equipotential surfaces are closer and weak where
the surfaces are apart.
4) No two equipotential surface intersect each other

8. 2.Electrostatic Potential And Capacitance
Page 25
Relation between field and potential(3 marks):-
Consider two closely spaced equipotential
surfaces A and B with potential values V and
V + dV, where dV is the change in V in the
direction of the electric field E.
Let P be a point on the surface B. δl is the
perpendicular distance of the surface A from P.
Let a unit test charge 𝑞𝑜 is moving from B to
A, then force on charge is
𝐹 = 𝑞𝑜𝐸
⃗ ……………(1)
The work done in moving charge from B to A is
𝑑𝑤 = 𝑞𝑜(𝑉𝐴 − 𝑉𝐵)= 𝑞𝑜(𝑉 − 𝑉 − 𝑑V)= −𝑞𝑜𝑑V..(2)
But
work done =Force x displacement
𝑑𝑤 = 𝐹. 𝑑𝑙 ……(3)
Substituting equation 91) abd (2) in eqn.(3) we get
−𝑞𝑜𝑑V = 𝑞𝑜𝐸
⃗⃗⃗ 𝑑𝑙
𝑬
⃗⃗ = −
𝒅𝑽
𝒅𝒍
Negative sign indicates that Potential decreases in the direction of electric field.
POTENTIAL ENERGY OF A SYSTEM OF CHARGES
Electrical potential energy of a system of point charges may be defined as the amount
of work done in assembling the charges at their respective location from infinity.
1)Potential energy of a system of TWO charges q1 and q2 in the absence of external
electric field:- (3 mark)
Consider two location P1 and P2 in space. Let a charge 𝑞1 brought from infinity to 𝑃1,to
do this no work id done because there is no electric field yet.
Now electrical potential due to charge 𝑞1 at point 𝑃2 at distance 𝑟12 from 𝑃1 is
𝑞1 𝑞2
𝑃1 𝑃2
𝒓𝟏𝟐
W1 = 0
∞

9. 2.Electrostatic Potential And Capacitance
th Page 26
𝑃3
𝑃1
𝑃2
V1 =
q1
4πε0r12
Hence work done in bringing a charge 𝑞2 from infinity to point 𝑃2is
W2 = Potential × charge
W2 = V1 × q2
W2 =
q1q2
4πε0r12
Hence the net work done is by the two charges is stored in the form of electrical potential
energy
U = W1 + W2
𝐔 =
𝐪𝟏𝐪𝟐
𝟒𝛑𝛆𝟎𝐫𝟏𝟐
2)Potential energy of a system of THREE charges q1 q2 and q3 in the absence of
external electric field:- (3 mark)
Let a charges 𝑞1 brought from infinity to 𝑃1 ,to do this no work is done because there is
no electric field yet.
Now electrical potential due to charge 𝑞1 at point 𝑃2 at distance 𝑟12 from 𝑃1 is
V1 =
q1
4πε0r12
Hence work done in bringing a charge 𝑞2 from infinity to point 𝑃2is
W2 = Potential × charge
W1 = 0

10. th Page 27
W2 = V1 × q2
W2 =
q1q2
4πε0r12
Now electrical potential due to charges 𝑞1 and 𝑞2 at point 𝑃3is sum of the potentials
V3 =
q1
4πε0r13
+
q2
4πε0r23
And work done to bring charge 𝑞3 from infinity to point 𝑃3 is
W3 = V3 × q3 = [
q1
4πε0r13
+
q2
4πε0r23
] × q3
W3 =
q1q3
4πε0r13
+
q2q3
4πε0r23
Hence the net work done is by the three charges is stored in the form of electrical potential
energy
U = W1 + W2 + W3
U = 0 +
q1q2
4πε0r12
+
q1q3
4πε0r13
+
q2q3
4πε0r23
Note:-1) This unit of electrical potential energy is electron volt or ‘eV’.(1 mark)
2)1eV=1.6 × 10–19J. (1 mark)
3) Solve numerical number 2.5 from NCERT text book.
POTENTIAL ENERGY IN AN PRESENCE OF EXTERNAL FIELD
1)Potential energy of a single charge:-
The potential energy of the charge q in the field is equal to the work done in bringing the
charge from infinity to the point. Now, we know that the potential at infinity is always taken
to be zero; the work done in bringing a charge from infinity to the point is given as,
U= qV
𝐔 =
𝟏
𝟒𝛑𝛆𝟎
(
𝐪𝟏𝐪𝟐
𝐫𝟏𝟐
+
𝐪𝟐𝐪𝟑
𝐫𝟐𝟑
+
𝐪𝟑𝐪𝟏
𝐫𝟑𝟏
)
2.Electrostatic Potential And Capacitance

11. 2.Electrostatic Potential And Capacitance
th Page 28
2)Potential energy of a system of two charges in an external field
Let us consider a system of two charges 𝑞1 and 𝑞2 located at a distance 𝑟1 and
𝑟2 from the origin. Let these charges be placed in an external field of magnitude E.
Let the work done in bringing the charge 𝑞1 from infinity to 𝑟1 be given as
W1 = 𝑞1𝑉(𝑟1)
The work done in bringing the charge 𝑞2 from infinity to 𝑟2 against the external field
can be given as
W2= 𝑞2𝑉(𝑟2)
We note that, 𝑞2 has to bring from infinity to 𝑟2 in the electric field due to 𝑞1 along
with the external electric field E, then work done in this case given as,
W3 =
q1q2
4πε0r12
Here, r12 is the distance between 𝑞1 and 𝑞2 .We can add these two to get the total work
done in bringing q2 from infinity to r2.
Thus, the total work done required to bring both the charges from infinity to the
present configuration or the total potential energy of the system can be given as
𝐔 = 𝒒𝟏𝑽(𝒓𝟏) + 𝒒𝟐𝑽(𝒓𝟐) +
𝐪𝟏𝐪𝟐
𝟒𝛑𝛆𝟎𝐫𝟏𝟐
Practice below diagrams
𝐔 = 𝒒𝟏𝑽(𝒓𝟏) + 𝒒𝟐𝑽(𝒓𝟐) +
𝐪𝟏𝐪𝟐
𝟒𝛑𝛆𝟎𝐫𝟏𝟐

12. 2.Electrostatic Potential And Capacitance
th Page 29
POTENTIAL ENERGY OF A DIPOLE IN AN EXTERNAL FIELD(5 marks)
Consider a dipole placed in a uniform electric field(E), the dipole experiences no net
force; but experiences a torque(τ) ,which will tend to rotate it (unless p is parallel or
antiparallel to E).
𝝉 = 𝒑 × 𝑬
Let an external torque ( 𝝉𝒆𝒙𝒕 = 𝑷𝑬𝒔𝒊𝒏𝜭) is required to neutralize the torque (𝝉) due to
electric field and must be equal in magnitude. Let the dipole rotated from and angle 𝜃0 to 𝜃1
.The amount of work done by the external torque will be given by,
𝑊 = ∫ 𝜏𝑒𝑥𝑡
𝜃1
𝜃0
∙ 𝑑𝜃
𝑊 = ∫ 𝑃𝐸𝑠𝑖𝑛𝛳
𝜃1
𝜃0
∙ 𝑑𝜃 = 𝑃𝐸 ∫ 𝑠𝑖𝑛𝛳
𝜃1
𝜃0
∙ 𝑑𝜃
𝑊 = 𝑃𝐸(cos 𝜃0 − cos 𝜃1)
This work is stored as the potential energy of the system
𝑼 = 𝑷𝑬(𝐜𝐨𝐬 𝜽𝟎 − 𝐜𝐨𝐬 𝜽𝟏)
Now when 𝜃0 =
𝜋
2
and 𝜃1 = 𝜃 where the potential energy is zero can be taken as reference
angular position. Then 𝑼 = 𝑷𝑬(𝐜𝐨𝐬
𝝅
𝟐
− 𝐜𝐨𝐬 𝜽) = −𝑷𝑬 𝐜𝐨𝐬 𝜽

13. 2.Electrostatic Potential And Capacitance
th Page 30
Note:-
1) When θ = 0 , i.e., P is aligned in the direction of E, potential energy is minimum.(1 mark)
2)When θ = π , i.e., P is aligned in the opposite direction of E, potential energy is maximum.
ELECTROSTATIC PROPERTIES OF CONDUCTORS
Conductors contain mobile charge carriers. In metallic conductors, these charge
carriers are electrons. In a metal, the outer (valence) electrons part away from their atoms
and are free to move. These electrons are free within the metal but not free to leave the
metal.
In an external electric field, they drift against the direction of the field. The positive
ions made up of the nuclei and the bound electrons remain held in their fixed positions. In
electrolytic conductors, the charge carriers are both positive and negative ions. Some of
the important points about the electrostatic properties of a conductor are as follows:
1)The electrostatic field is zero inside a conductor.
2) Electrostatic field lines are normal to the surface at every point in a charged conductor.
3) In the static conditions, the interior of the conductor contains no excess charge.
4) The electrostatic potential at any point throughout the volume of the conductor is always
constant and the value of the electrostatic potential at the surface is equal to that at any
point inside the volume.
5) Electric field at the surface of a charged conductor is E =
𝝈
𝜺𝟎
where σ, surface charge density.
ELECTROSTATIC SHIELDING:- (1 mark)
The phenomenon of making a region free from any electric field is called electrostatic
shielding.
Applications:-
1) In lightening thunderstorm, it is safe to sit inside the car, rather than near a tree or in
open ground. The metallic body of the car acts as electrostatic shielding from lightening.
2) In coaxial cable, the central conductor is protected by electrostatic shield by connecting
the outer conductor to the ground.
DIELECTRICS AND POLARISATION:-
Dielectrics are non-conducting substances. They are the insulating materials and are
bad conductors of electric current. Dielectric materials can hold an electrostatic charge.
Examples: Mica, Plastics, Glass, Porcelain and Various Metal Oxides. You must also remember
that even dry air is also an example of a dielectric

14. 2.Electrostatic Potential And Capacitance
th Page 31
Classification of Dielectrics
1. Polar Molecules: Polar molecule in which the centre of positive and negative charges
are separated (even when there is no external field).
Examples: H2O, CO2, NO2 etc.
The molecule has permanent (or intrinsic) dipole moment.
When the electric field is not present, it causes the electric dipole moment of
these molecules in a random direction. This is why the average dipole moment is zero.
If the external electric field is present, the molecules assemble in the same
direction as the electric field.
2. Non-Polar Molecule: Unlike polar molecules, in non-polar molecules, the centre of
positive charge and negative coincide.
Examples: O2, N2, H2 etc.
The molecule then has no permanent (or intrinsic) dipole moment.
Polar Molecules behavior in electric field
Non-Polar Molecules behavior in electric
field

15. 2.Electrostatic Potential And Capacitance
th Page 32
𝝌
POLARISATION :Polar or non-polar, a dielectric develops a net dipole moment in the
presence of an external field. The dipole moment per unit volume is called polarisation and
is denoted by P. For linear isotropic dielectrics,
P = eE
Where Xe is a constant characteristic of the dielectric and is known as the electric
susceptibility of the dielectric medium.
CAPACITORS AND CAPACITANCE
 A capacitor is a system of two conductors separated by an insulator.
 The capacitor is an electrical component that has the ability to store energy. The
energy is stored in the form of electric charge.
 The total charge of the capacitor is zero.
 The electric field in the region between the conductors is proportional to the charge Q.
 The potential difference V is the work done per unit positive charge in taking a small
test charge from the conductor 2 to 1 against the field.
 Consequently, V is also proportional to Q, and the ratio Q/V is a constant:
𝐂 =
𝐐
𝐕
The constant C is called the capacitance of the capacitor. C is independent of Q or V.
+Q
-Q

16. 2.Electrostatic Potential And Capacitance
th Page 33
Note:-
1)The capacitance C depends only on the only on the geometrical configuration (shape,
size, separation) of the system of two conductors.
2)The S.I. unit of capacitance is Farad.(F)
3)1Farad= 1Coulomb per volt.(1F=1CV-1)
THE PARALLEL PLATE CAPACITOR(5 marks)
(Derive the expression for the capacitance of parallel plate capacitor absence of
dielectric medium.)
A parallel plate capacitor consists of two large plane parallel conducting plates separated
by a small distance.
Let a parallel plate capacitor where each plate having an area A and d the separation
between them. The two plates have charges Q and –Q. Plate 1 has surface charge density
σ=Q/A and plate 2 has a surface charge density σ=–Q/A.
From Gauss law, we know that electric field due to a
plane charged sheet is,
E =
σ
ε0
In the inner region between the plates 1 and 2, the
electric fields due to the two charged plates added,
E =
σ
2ε0
+
σ
2ε0
=
σ
ε0
but σ = 𝑄/𝐴
E =
Q
ε0A
Now for uniform electric field, potential difference is simply the electric field times the
distance between the plates, that is,
𝑉 = 𝐸𝑑 =
Q
ε0A
𝑑.......................(1)
but from definition of the capacitance
C =
Q
V
… … … … … … … … … … … … . (2)
from equation (1) and (2) we get
𝑪 =
𝜺𝟎𝑨
𝒅

17. 2.Electrostatic Potential And Capacitance
th Page 34
The capacitance C of parallel plate capacitor depends only on the:(3 marks)
1) Dielectric constant of medium between plates
The effect of dielectric on capacitance is that the capacitance value increases when the
dielectric is either constant or when the relative permittivity is large. Air acts as a dielectric
between the two parallel plates.
2)Spacing on the capacitance between the two plates
The effect of spacing on the capacitance is that it is inversely proportional to the distance
between the two plates. Mathematically it is given as:
𝐶 ∝
1
𝑑
3) Area of the plate on the capacitance
The effect of area of the plate is that the capacitance is directly proportional to the area.
Larger the plate area more is the capacitance value. Mathematically it is given as:
𝐶 ∝ 𝐴
EFFECT OF DIELECTRIC ON CAPACITANCE
(Derive the expression for the capacitance of parallel plate capacitor presence of
dielectric medium of constant 'K')
Capacitor with parallel plates of area A, separated by a distance d, the charge on
each plate is +Q and –Q. The corresponding charge density can be given as ±σ. Where, then
capacitance when the medium between the plate is vacuum is given by,
𝑪𝟎 =
𝜺𝟎𝑨
𝒅
As the dielectric medium is inserted between the plates, it gets polarized by the field and
the charges get arranged such that they act as two charged sheets with a surface charge
density of σp and – σp, as shown in the figure below
The net surface charge density then becomes equivalent to ±(σ – σp)
Dielectric slab

18. 2.Electrostatic Potential And Capacitance
th Page 35
E =
(σ – σp)
ε0
Hence potential difference across the plate is
𝑉 = 𝐸𝑑 =
(σ – σp)
ε0
𝑑
But σp is directly proportional to 𝐸0,
(σ – σp) =
σ
K
Where ‘K’ is a constant characteristic of the dielectric
𝑉 =
σ𝑑
ε0K
=
Q𝑑
Aε0K
But C =
Q
V
C =
𝜺𝟎𝑲𝑨
𝒅
Where 𝜀0𝐾 = 𝜀 called permittivity of medium,
Hence 𝐾 =
𝜺
𝜺𝟎
𝐂 = 𝑪𝟎𝑲
From above equation depict that by inserting dielectric medium between the plate can
increase the capacitance by ‘K’ times that of capacitance in vacuum.

19. 2.Electrostatic Potential And Capacitance
th Page 36
COMBINATION OF CAPACITORS
Capacitors in series:- When capacitors are connected in series, the magnitude of
charge Q on each capacitor is same. The potential difference across C1 and C2 is different
i.e., V1 and V2
We know Q = C1 V1 = C2 V2
For equivalent circuit Q = CV
The total potential difference across combination is
V = V1 + V2
𝑄
𝐶𝑒𝑞
=
𝑄
𝐶1
+
𝑄
𝐶2
The equivalent capacitance is
𝟏
𝑪𝒆𝒒
=
𝟏
𝑪𝟏
+
𝟏
𝑪𝟐
In case of more than two capacitors, the relation is:
1
𝐶𝑒𝑞
=
1
𝐶1
+
1
𝐶2
+
1
𝐶3
… … .
1
𝐶𝑛
 When capacitors are connected in series their resultant capacitance 𝐶𝑒𝑞 is the sum of
the reciprocal of individual capacitances.
 The value of equivalent capacitance of system is smaller than the individual one.
𝐶𝑛
𝐶3
𝐶2
𝐶1
Q Q Q Q -Q
-Q
-Q
-Q

20. 2.Electrostatic Potential And Capacitance
th Page 37
Parallel combination of capacitors :-When capacitors are connected in parallel, the
magnitude of potential on each capacitor is same. The charge stored in each capacitor
is different Q1 and Q2.
 When capacitors are connected in parallel their resultant capacitance 𝐶𝑒𝑞 is the sum
of the individual capacitances.
 The value of equivalent capacitance of system is larger than the individual one.
As we know 𝐶 =
Q
V
apply this equation on each capacitor
𝑄1 = 𝐶1𝑉 and 𝑄2 = 𝐶2𝑉
For equivalent circuit 𝑄 = 𝐶𝑒𝑞𝑉
The equivalent capacitor is one with charge
Q = Q1 + Q2
Q = 𝐶𝑒𝑞V = C1V + C2V
The effective capacitance 𝑪𝒆𝒒 = C1 + C2
The general formula for effective capacitance C for
parallel combination of n capacitors is,
Q = Q1 + Q2 + ... + Qn
i.e., CV = C1V + C2V + ... CnV
which gives C = C1 + C2 + ... Cn
-Q1
-Q2
-Qn
+Q1
+Q2
+Qn
C1
C2
Cn

21. 2.Electrostatic Potential And Capacitance
th Page 38
ENERGY STORED IN A CAPACITOR: Capacitor store the energy in the form of charge.
Basically it build the electric field between the plates. Let a capacitor has ±q charge on its
plate at any instant of time 't' .
Now a small charge dq moving from one plate to another plate in time dt.
Then potential across plate is given by
V=
𝑞
𝐶
hence work done by moving charge dq is given by
dw = Vdq by definition of potential
dw=
𝑞
𝐶
𝑑𝑞
The work done in charging capacitor fully i.e. up to charge Q is given by
Integrating above equation from limit 0 to Q
∫ 𝑑𝑤 = ∫
𝑞
𝐶
𝑑𝑞
𝑄
0
𝑈
0
=
1
𝐶
∫ 𝑞. 𝑑𝑞
𝑄
0
Q
𝑈 =
1
𝐶
[
𝑞2
2
]
𝑈 =
1
𝐶
[
𝑄2
2
−
02
2
]
𝑼 =
𝑸𝟐
𝟐𝑪
but Q=CV
0
dq
−𝑞
+𝑞
𝑼 =
𝟏
𝟐
𝑪𝑽𝟐

22. 2.Electrostatic Potential And Capacitance
th Page 39
1)Energy stored in the capacitor
𝑼 =
𝑸𝟐
𝟐𝑪
=
(𝑨𝝈)𝟐
𝟐
×
𝒅
𝑨𝜺𝟎
2)The surface charge density 𝝈 is related to the electric field E between the plates
𝑬 =
𝝈
𝜺𝟎
3) Energy stored in the capacitor from 1 and 2 we get
𝑼 =
𝟏
𝟐
𝜺𝟎𝑬𝟐
× 𝑨𝒅
4)Energy density is defined as energy stored per unit volume of space.
𝑼 =
𝟏
𝟐
𝜺𝟎𝑬𝟐

23. 2.Electrostatic Potential And Capacitance
th Page 40

24. 2.Electrostatic Potential And Capacitance
th Page 41
1. Define electric potential energy.
2. Is the work done by electrostatic field in moving a charge from one point to another
depend on the path that it moves?
3. While defining the electrostatic potential due to a point charge, the reference of unit
positive charge moving from infinity is considered. Why?
4. Define electrostatic potential at a point.
5. Mention SI unit of electric potential.
6. Write the expression for work done in moving a charge from one point to another in an
electric field.
7. Write the expression for electric potential due to a point charge.
8. How does electric potential due to a point charge vary with distance from it?
9. How does electric potential due to a short electric dipole vary with distance?
10. What is the potential at a point which is at a distance of 9 cm from a point charge 1nC?
11. What is the work done in bringing a charge of 3mC through a potential difference of
4000 V?
12. What is the electric potential inside a uniformly charged spherical shell?
13. Write the expression for electric potential due to system of charges.
14. What is an equipotential surface?
15. Draw equipotential surfaces for a uniform electric field.
16. Draw equipotential surfaces for a dipole.
17. Draw equipotential surfaces for two identical positive charges.
18. What is the work done to move a charge from one point to another point on an
equipotential surface?
19. Write the relation between the electric field and potential.
20. Write the expression for potential energy of system of three charges.
21. Define potential energy of a point charge ‘q’ kept in an external electric field.
22. Define electron volt.
23. Write the energy equivalence between electron volt and joule.
24. Write the expression for potential energy of system of two charges in an external
electric field.
25. What are the charge carriers in electrolytic conductors?
26. What is the value of electrostatic field inside a charged conductor?
27. What is the direction of electric field on the surface of a charged conductor?
28. What is electrostatic shielding?
29. Where electrostatic shielding is made use of?
30. What is a dielectric?
31. What is polarization of a dielectric?
32. Define electric capacitance of a capacitor.
ONE MARK QUESTIONS

25. 2.Electrostatic Potential And Capacitance
Page 42
33. What is a capacitor?
34. Draw the circuit symbol of a capacitor.
35. Draw the circuit symbol of a variable capacitor.
36. Give SI unit of electrical capacitance.
37. Define dielectric strength of a dielectric medium.
38. Mention the SI unit of dielectric strength.
39. What is the value of dielectric strength of air?
40. Define farad, the unit of capacitance.
41. Write the expression for electric field between the two plates of parallel plate capacitor.
42. Express dielectric constant in terms of permittivity of free space.
43. Write the expression for equivalent of capacitance of two capacitors connected in series
combination.
44. Write the expression for equivalent capacitance of two capacitors connected in parallel
combination.
45. Write the expression for energy stored in a capacitor.
46. Which form of energy is stored in the capacitor?
47. Write the expression for energy stored in the capacitor in terms of electric field.
1. Draw the curves representing the variation of electrostatic potential and field with the
distance from a point charge.
2. Find the potential at a point P due to a charge of 4×10-9 C located 9 cm away from it.
3. Write the expression for the potential at any point due to an electric dipole and explain
the terms.
4. What work is done in moving any charge from the center of a charged spherical shell to
any point inside it? Justify your answer.
5. Distinguish between polar and non-polar dielectrics.
6. What are the factors on which capacitance of a capacitor depend?
7. Write the expression for capacitance of a parallel plate capacitor and explain the terms.
8. A material of dielectric constant 2 is inserted between the plates of a capacitor 3 micro
F. calculate the new value of the capacitance.
9. Find the energy stored in a capacitor of capacitance 5nF when connected to a potential
of 6V source.
10. Write the expression for energy density in case of a charged capacitor and explain the
symbols used.
TWO MARK QUESTIONS

26. 2.Electrostatic Potential And Capacitance
Page 43
1. Derive the expression for potential due to a system of charges.
2. Obtain the expression for the relation between electric field and electric potential.
3. Arrive at the expression for the potential energy of a system of two charges in the
absence of an external electric field.
4. Obtain the expression for the potential energy of a system of two charges in the
presence of an external electric field.
5. Capacitance of a parallel plate capacitor is 1F and the plates are separated by 1cm. Find
the area of each plate of the capacitor.
6. Obtain an expression for the capacitance of a parallel plate capacitor.
7. Derive the expression for the effective capacitance of a series combination of two
capacitors.
8. Arrive at the expression for the effective capacitance of a parallel combination of two
capacitors.
9. Derive the expression for the energy stored in a capacitor.
1. Define electrostatic potential due to a point charge and arrive at the expression for
electric potential at a point due to a point source charge.
2. Obtain the expression for electrostatic potential at any point due to a short electric
dipole.
3. List out the important results regarding the (static charges) electrostatics of a
conductor.
4. Arrive at the expression for the capacitance of a parallel plate capacitor when a
dielectric is introduced between its plates.
1. PQRS is a square of side 1m. Four charges +10nC, -20nC, +30nC & +20nC are placed at
the corners PQRS respectively. Calculate the electric potential at the intersection of the
diagonals. [509V]
2. Charges +2nC, +4nC, and +8nC are placed at the corners ABC respectively of a square of
side 0.2m. Calculate the work done to transfer a charge of +2nC from the corner D to the
center of thesquare. [627.4X10-9J]
3. A battery of 10V is connected to a capacitor of capacitance 0.1F. The battery is now
removed and this capacitor is connected to a second uncharged capacitor. If the charge
distributes equally on these two capacitors, find the total energy stored in each
capacitor, and compare with the initial energy of the first capacitor. [2.5J, 0.5 times]
Three mark questions
Five mark questions
Numerical problems

27. 2.Electrostatic Potential And Capacitance
Page 44
4. A spherical drop of water carrying a charge of 3 X10-10C has a potential of 500V at its
surface. Find the radius of the drop. If two such drops of the same charge and radius
combine to form a single spherical drop, calculate the potential at the surface of the new
drop. [ 5.4X10-3m, 794V]
5. Two capacitors of capacitances 2µF and 8µF are connected in series and the resulting
combination is connected across a 300V battery. Calculate the charge, potential
difference and the energy stored in each capacitor.
[Charge=4.8X10-4C, Potential=240V, 60V, Energy=5.76X10-2J &1.44X10-2J]