This document summarizes a PhD thesis on wind effects in tensile membrane structures. It discusses form-finding methods like the force density method and dynamic relaxation method. It then applies these to analyze a tensile membrane roof and develop a real-time form-finding method for boat sails using fiber optic sensors. For the roof, it examines the effects of prestress, orthotropic properties, and wind through numerical simulation. It also validates the sail form-finding using image-based systems to address uncertainties in fiber optic technology. The thesis contributes methods to analyze membrane structures and assess wind effects in addition to developing a patented real-time sail monitoring algorithm.

1. Wind Effects in Tensile
Membrane Structures
Pedro Gil Marques de Queirós Ferreira
Elsa de Sá Caetano
2016

2. PhD 2016 | 2
2016 CONSTRUCT PhD Workshop
Wind Effects in Tensile Membrane Structures
• Motivation
– Growing use of tensile membranes in special
structures has brought increased demand in the
assessment of their structural behavior
– Membrane structures are characterized by: high
flexibility, leading to strong geometric nonlinear
behavior; complex shapes; slight prestress;
orthotropic materials; and construction methods
– Recent damages due to aerodynamic and
ponding effects of these lightweight structures
and lack of standards motivated this work

3. PhD 2016 | 3
2016 CONSTRUCT PhD Workshop
Wind Effects in Tensile Membrane Structures
• Objectives & Tasks
– The work focused two main aspects
• Form-finding
• Characterization of the wind effects in membranes
– Two types of examples
• Roof of a multisport arena
– Role of prestress & orthotropy on structural behavior
– Wind effects considering generation of stochastic wind
loads and numerical evaluation of membrane response
through a simplified model, characterizing the
aerodynamic mass, stiffness and damping
• 470 Sailboat
– Develop and validate a methodology of form-finding of
a boat sail in real-time based on strain measurements
• Case studies
– Roof
– Sailboat

4. PhD 2016 | 4
2016 CONSTRUCT PhD Workshop
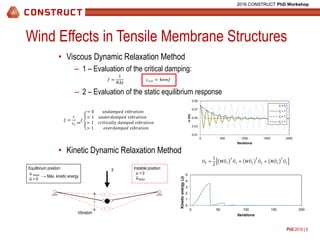
Wind Effects in Tensile Membrane Structures
– Structural form-finding and optimization methods
• Force Density Method (FDM): 1lFDM and 2nlFDM
– Independent of the material properties and linearize the
Equilibrium equations using a force density coefficient q
= t/l for the truss elements
• Surface Stress Density Method
– Analogous to FDM setting a surface stress density
coefficient qs for the constant strain triangle elements
• Dynamic Relaxation Method: Viscous & Kinetic model
– Explicit direct time-integration of the dynamic
Equilibrium equations using central finite differences.
[Cs Xf q F]1,2 + Qz
2 X t l
Cs Xf Xini qs F Xend t l S σ = 4qsS
Cs Xf Xini F (E A ti )truss el. Xend t l
kN/m
0 2 4 6 8 10
0
1
2
3
4
5
6
7
8
9
10
1 2
3
4 5
6
7 8
9
Geometria Inicial - MDFl
x
y
0 2 4 6 8 10
0
1
2
3
4
5
6
7
8
9
10
1
2
3
4 5
6
7 8
9
Geometria Inicial - MDFl
x
y
0 2 4 6 8 10
0
1
2
3
4
5
6
7
8
9
10
1
2
3
4 5
6
7 8
9
Geometria Inicial - MDFl
x
y
0 2 4 6 8 10
0
1
2
3
4
5
6
7
8
9
10
1 2
3
4 5
6
7 8
9
Geometria Inicial - MDFl
x
y

5. PhD 2016 | 5
2016 CONSTRUCT PhD Workshop
Wind Effects in Tensile Membrane Structures
• Linear Force Density Method (lFDM)
– Example of a cooling tower
 Solution is obtained iteratively: rinf ≈ 9
m, rsup ≈ 7 m, Hc ≈ 21 m e Hm ≈ 25 m
Configuração a) b) c)
qs (N/m) 400 400 400
qcomp (N/m) -2800 -3000 -3000
qc,v (N/m) 100 100 1000
qc,h (N/m) 100 100 100
Configuração a) b) c)
qs (N/m) 400 400 400
qcomp (N/m) -2800 -3000 -3000
qc,v (N/m) 100 100 1000
qc,h (N/m) 100 100 100
Suspension cables
Upper compression ring
Lateral cable net (horizontal
or circumferential and vertical
cables)
Mast
Lower compression ring

6. PhD 2016 | 6
2016 CONSTRUCT PhD Workshop2016 CONSTRUCT PhD Workshop
Wind Effects in Tensile Membrane Structures
• Viscous Dynamic Relaxation Method
– 1 – Evaluation of the critical damping:
– 2 – Evaluation of the static equilibrium response
• Kinetic Dynamic Relaxation Method
𝑓 =
1
𝑁∆𝑡
𝑐 𝑐𝑟𝑖𝑡 = 4𝜋𝑚𝑓
𝑈𝑘 =
1
2
𝑀𝑈𝑥
𝑇
𝑈𝑥 + 𝑀𝑈𝑦
𝑇
𝑈𝑦 + 𝑀𝑈𝑧
𝑇
𝑈𝑧
0
1
2
3
4
5
0 50 100 150 200
Kineticenergy(J)
Iterations
0.01
0.03
0.05
0.07
0.09
0 500 1000 1500 2000
u(m)
Iterations
ξ = 0
ξ < 1
ξ = 1
ξ > 1
Equilibrium position:
→ Máx. kinetic energy
𝑢 𝑚á𝑥
𝑢 = 0
Instable position:
𝑢 = 0
𝑢 𝑚á𝑥
Vibration
F
𝜉 =
𝑐
𝑐 𝑐
𝜉
= 0 𝑢𝑛𝑑𝑎𝑚𝑝𝑒𝑑 𝑣𝑖𝑏𝑟𝑎𝑡𝑖𝑜𝑛
< 1 𝑢𝑛𝑑𝑒𝑟𝑑𝑎𝑚𝑝𝑒𝑑 𝑣𝑖𝑏𝑟𝑎𝑡𝑖𝑜𝑛
= 1 𝑐𝑟𝑖𝑡𝑖𝑐𝑎𝑙𝑙𝑦 𝑑𝑎𝑚𝑝𝑒𝑑 𝑣𝑖𝑏𝑟𝑎𝑡𝑖𝑜𝑛
> 1 𝑜𝑣𝑒𝑟𝑑𝑎𝑚𝑝𝑒𝑑 𝑣𝑖𝑏𝑟𝑎𝑡𝑖𝑜𝑛

7. PhD 2016 | 7
2016 CONSTRUCT PhD Workshop
Wind Effects in Tensile Membrane Structures
– Roof of a multisport arena
• Tensile membrane roof structure located in Cartuja Island, Seville
• Doubly symmetric tubular metallic structure in plan, nearly rectangular in
plan 24 x 46 m2, including suspended cables and calibrated rods
• Tensile membrane made of PES/PVC, comprised by 4-top (hip. parab.)
and 4-lateral modules (flat)
Tubular section F 323x8 (mmxmm)
Tubular section F 200x6 (mmxmm)
Tubular section F 150x5 (mmxmm)
Cable F 36 mm
Calibrated rod F 25 mm
U – warp
T – fill

8. PhD 2016 | 8
2016 CONSTRUCT PhD Workshop
Wind Effects in Tensile Membrane Structures
– Roof of a multisport arena
• Form-finding of the membrane with prestress of 2 kN/m
through all implemented methods and specialized
software, and comparing the same premises of
orthotropic orientations, showed slightly different results
• Numerical simulation studies of the influence of the
prestress, orientation of orthotropic directions, and
Poisson coefficient evidenced significant differences on
the static and dynamic responses of the membrane
• Nonlinear dynamic analysis in time domain considering
geometric nonlinearity and large displacements showed
dynamic amplification coefficients Rdyn of about 0,8
• Identification of wrinkles on the corners of the lateral
modules due to non-economic shapes
0
1
2
3
4
5
6
7
0
20
40
60
80
100
120
140
160
0 10 20 30 40
Frequência(Hz)
Fatordeparticipação
Modo
X
Y
Z
Freq.
3.79
5.97
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
1.E-12
1.E-08
1.E-04
1.E+00
0 5 10 15 20
Fatordehibridização(FH)
Amplitude
Frequência (Hz)
Dir. x
FH
Participationfactor
Mode
Frequency(Hz)
Disp.(m)
Amplitude
Hybridizationfactor
Frequency (Hz)Time (s)
-0.002
-0.001
0.000
0.001
0.002
0.003
100 150 200 250 300
Deslocamento(m)
Tempo (s)
Rdin = 1.08
Ux, quasi-estático
Ux, din
quasi-static
0
5
10
15
20
25
30
35
40
45
50
0 100 200 300 400 500 600 700 800
Velocidade(m/s)
Tempo (s)
1
534
Velocity(m/s)
Time (s)

9. PhD 2016 | 9
2016 CONSTRUCT PhD Workshop
Wind Effects in Tensile Membrane Structures
– Form-finding of a boat sail in real-time
• This work describes a monitoring system based
on fiber optic strain gauge sensors used to
reconstruct in real time the form of a sail
• The installation of FBG sensors on a beam allows
to obtain curvatures in specific cross-sections,
and evaluate, by interpolation, the coordinates of
the deformed beam and consequently the most
significant parameters of the sail shape
• Uncertainties related to optical technology,
require the calibration and validation of the results
through an alternative system.
• Since large amplitudes of deformations are
measured, the fiber optic monitoring system was
validated based on a imaging based system
Draft position
Chord
Camber(cm)
(%)(cm)

10. Conclusions
• Implementation of form-finding routines
• Application to a tensile membrane roof
• Identification of more relevant aspects of
the behavior through parametric analysis
• Wind action and effects assessment
• Sail case: development, implementation
and validation of an algorithm already
patented for real-time assessment of sail
shape. This methodology can be used for
SHM of other engineering applications