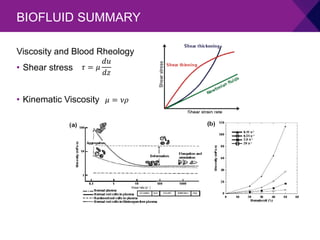
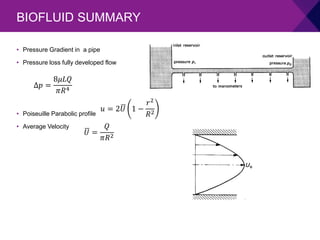
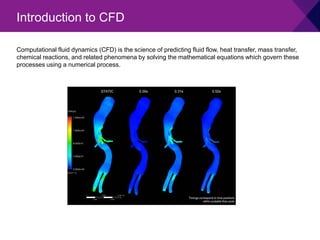
The document discusses computational fluid dynamics (CFD) and its advantages and limitations. CFD uses numerical methods to solve equations that govern fluid flow, heat transfer, and other related phenomena. It allows for inexpensive and fast simulations of real or ideal conditions to obtain comprehensive flow parameter data, though solutions depend on the accuracy of the physical models and boundary conditions used.

1. Dr Patrick Geoghegan
Book: H. Versteeg and W. Malalasekera An Introduction to
Computational Fluid Dynamics: The Finite Volume Method Chapter 2
FEA/CFD for
Biomedical
Engineering
Week 8: CFD –
Continuity

2. BIOFLUID SUMMARY

3. 1st Year revision
• Hydrostatic Pressure
• Conservation of mass
• Bernoulli equation
BIOFLUID SUMMARY
𝑝𝑝1 − 𝑝𝑝2 = 𝜌𝜌𝜌𝜌𝜌
̇
𝑚𝑚 = 𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐 = 𝜌𝜌1𝐴𝐴1𝑢𝑢1 = 𝜌𝜌2𝐴𝐴2𝑢𝑢2
𝑝𝑝1 +
1
2
𝜌𝜌𝑢𝑢1
2
+ 𝜌𝜌𝑔𝑔ℎ1 = 𝑝𝑝2 +
1
2
𝜌𝜌𝑢𝑢2
2
+ 𝜌𝜌𝑔𝑔ℎ2

4. Viscosity and Blood Rheology
• Shear stress
• Kinematic Viscosity
BIOFLUID SUMMARY
𝜏𝜏 = 𝜇𝜇
𝑑𝑑𝑑𝑑
𝑑𝑑𝑑𝑑
𝜇𝜇 = 𝜈𝜈𝜈𝜈

5. • Pressure Gradient in a pipe
• Pressure loss fully developed flow
• Poiseuille Parabolic profile
• Average Velocity
BIOFLUID SUMMARY
Δ𝑝𝑝 =
8𝜇𝜇𝜇𝜇𝜇𝜇
𝜋𝜋𝑅𝑅4
𝑢𝑢 = 2�
𝑈𝑈 1 −
𝑟𝑟2
𝑅𝑅2
�
𝑈𝑈 =
𝑄𝑄
𝜋𝜋𝑅𝑅2

6. • Boundary Layer
• Boundary layer thickness (u=0.99U)
• Pipe entrance length
• Reynolds Number
• For smooth pipes of circular cross section:
• Laminar flow: Re < ~2300-2500
• Transitional flow: ~2300-2500 < Re < 4000
• Turbulent flow: Re > 4000
BIOFLUID SUMMARY
𝑋𝑋 = 0.06𝑑𝑑 𝑅𝑅𝑅𝑅
𝑅𝑅𝑅𝑅 =
𝜌𝜌𝜌𝜌𝜌𝜌
𝜇𝜇
=
𝑈𝑈𝑈𝑈
𝜈𝜈
𝑅𝑅𝑅𝑅 =
𝑈𝑈𝑈𝑈
𝜈𝜈

7. Laminar Flow
• Path line each particles are parallel
• Low velocity
• Viscosity plays a significant part in laminar
• Velocity profile shown as parabolic curve
Turbulent Flow
• Particles are irregular path line
• High velocity
• Inertia plays a significant part in turbulent
• Velocity profile shown as logarithm curve
BIOFLUID SUMMARY

8. • Womersley Number
• Angular Frequency
• Flow rate in a venturi
• Wall Shear Stress
Equation Overview
𝛼𝛼 =
𝑑𝑑
2
𝜔𝜔
𝜈𝜈
=
𝑑𝑑
2
𝜔𝜔𝜔𝜔
𝜇𝜇
𝜔𝜔 = 2𝜋𝜋𝜋𝜋 =
2𝜋𝜋
𝑇𝑇
𝑄𝑄 =
2∆𝑝𝑝
𝜌𝜌 ⁄
1 𝐴𝐴2
2
− ⁄
1 𝐴𝐴1
2
𝜏𝜏 = 𝜇𝜇 �
𝑑𝑑𝑑𝑑
𝑑𝑑𝑑𝑑 𝑧𝑧=0
0 0.2 0.4 0.6 0.8 1
200
400
600
800
1000
Re
t / τ
0 0.2 0.4 0.6 0.8 1
1.5
1.7
1.9
2.1
2.3
2.5
2.7
2.9
3.1
x 10
4
Pressure
(Pa)
0 0.2 0.4 0.6 0.8 1
1.5
1.7
1.9
2.1
2.3
2.5
2.7
2.9
3.1
x 10
4
Pressure
(Pa)

9. CFD Basics Part 1

10. Computational fluid dynamics (CFD) is the science of predicting fluid flow, heat transfer, mass transfer,
chemical reactions, and related phenomena by solving the mathematical equations which govern these
processes using a numerical process.
Introduction to CFD

11. The governing equations (Navier-Stokes, continuity, energy, etc.) have
been known for a long time, but to solve these manually is only possible
in the simplest of cases –hence CFD
Introduction to CFD
( ) ( ) ( ) Mx
S
u
x
p
u
t
u
+
∇
+
∂
∂
−
=
⋅
∇
+
∂
∂
grad
µ
ρ
ρ
u

12. Relatively low cost.
• Using physical experiments and tests to get essential engineering data for design can be expensive.
• CFD simulations are relatively inexpensive, and costs are likely to decrease as computers become
more powerful.
Speed.
• CFD simulations can be executed in a short period of time.
• Quick turnaround means engineering data can be introduced early in the design process.
Advantages of CFD

13. Ability to simulate real conditions.
• Many flow and heat transfer processes can not be (easily) tested, e.g.
hypersonic flow.
• CFD provides the ability to theoretically simulate any physical condition.
Ability to simulate ideal conditions.
• CFD allows great control over the physical process, and provides the ability to
isolate specific phenomena for study.
Advantages of CFD

14. Comprehensive information.
• Experiments only permit data to be extracted at a limited number of
locations in the system (e.g. pressure and temperature probes, heat
flux gauges, LDV, etc.).
• CFD allows the analyst to examine a large number of locations in the
region of interest, and yields a comprehensive set of flow parameters
for examination.
Advantages of CFD

15. Physical models.
• CFD solutions rely upon physical models of real world processes (e.g.
turbulence, compressibility, chemistry, multiphase flow, etc.).
• The CFD solutions can only be as accurate as the physical models on
which they are based.
Boundary conditions
• As with physical models, the accuracy of the CFD solution is only as
good as the initial/boundary conditions provided to the numerical model
Rubbish in = Rubbish Out!
Limitations of CFD