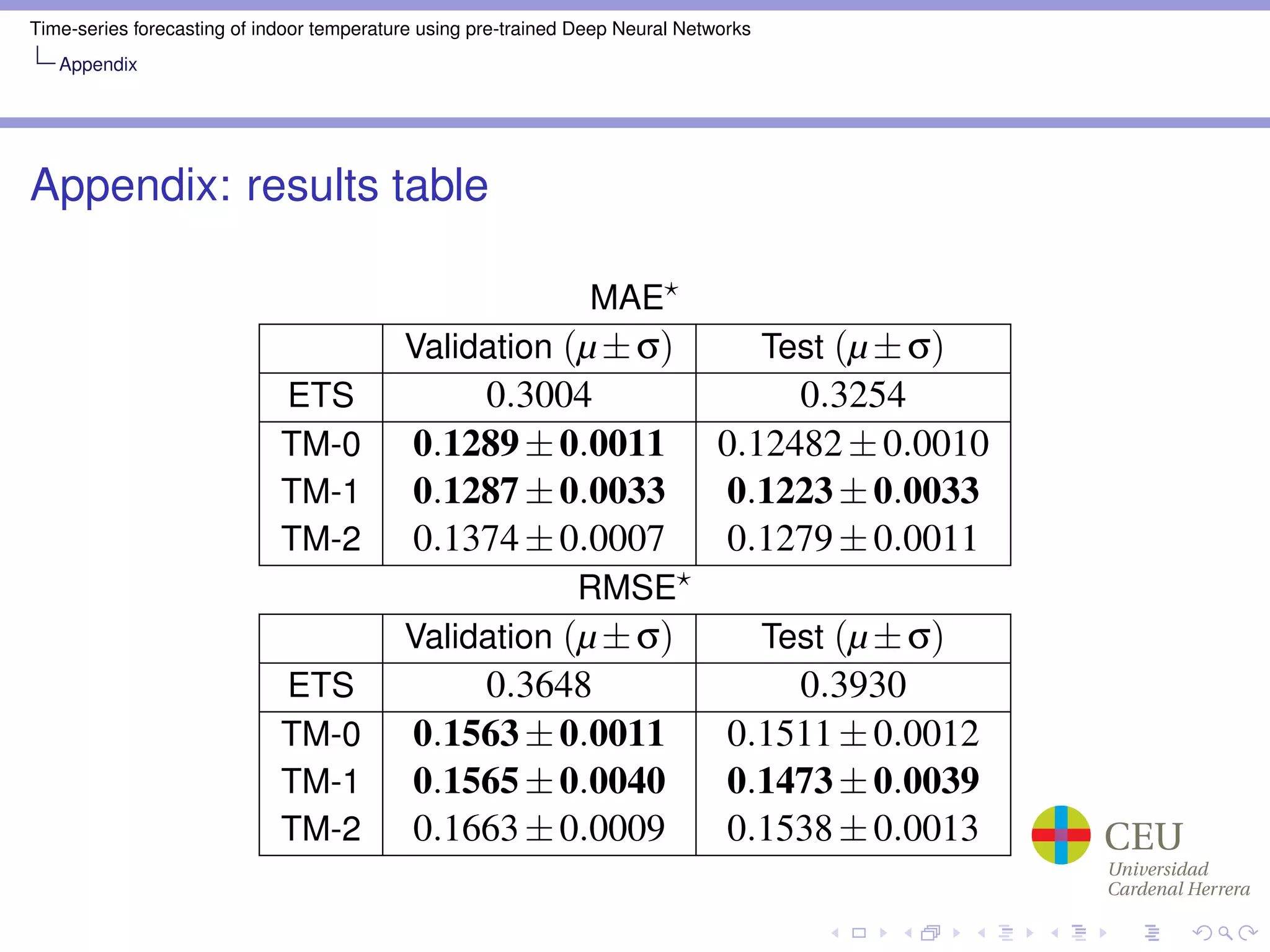
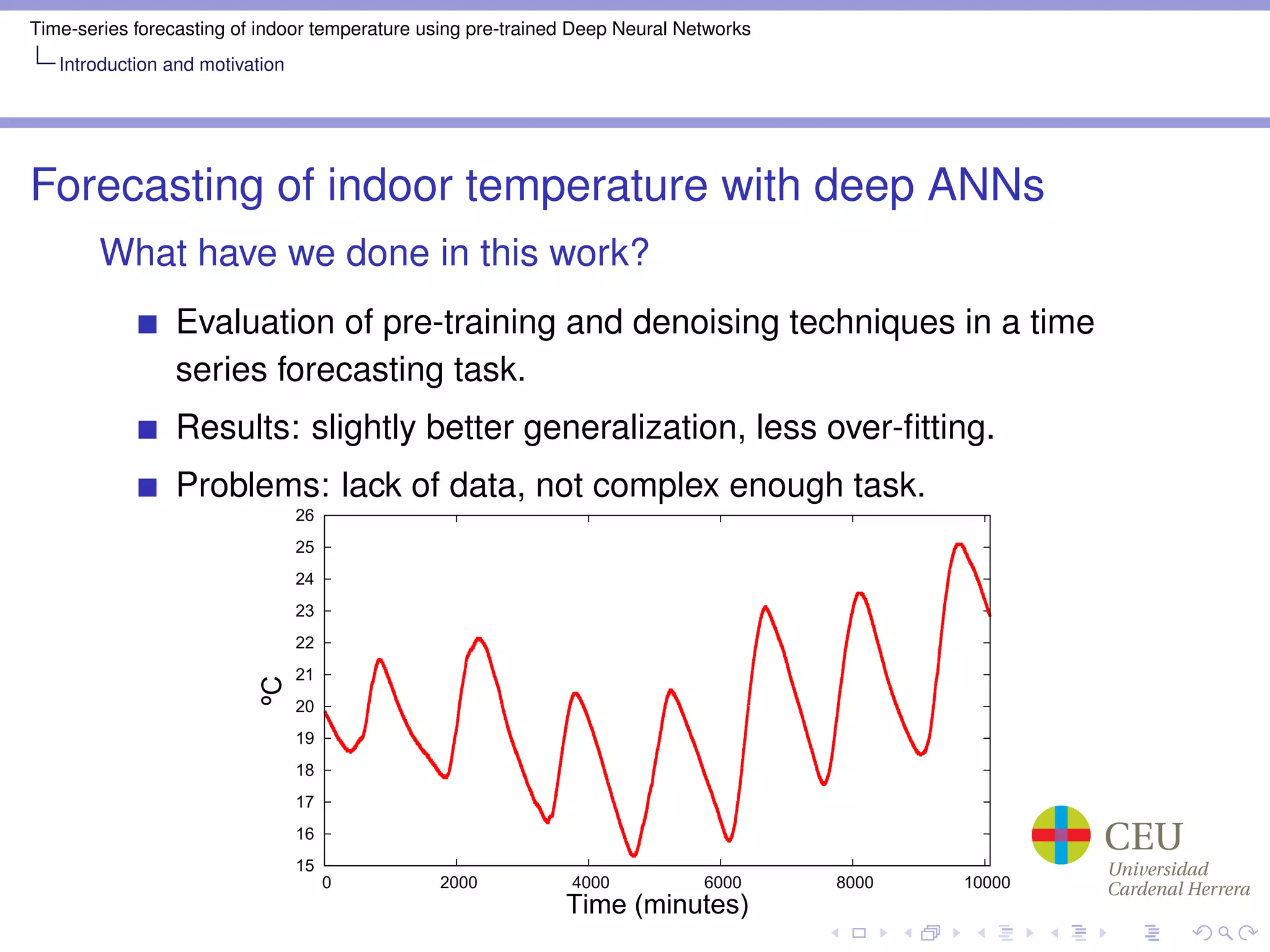
The document discusses time-series forecasting of indoor temperature using pre-trained deep neural networks, focusing on techniques such as stacked denoising auto-encoders and various training methods. Experiments showed improved generalization and less overfitting with pre-training, although limitations like sparse data were noted. Future work aims to enhance forecasting by increasing input window size and employing multivariate models.

1. Time-series forecasting of indoor temperature using pre-trained Deep Neural Networks
Time-series forecasting of indoor temperature
using pre-trained Deep Neural Networks
P. Romeu, F. Zamora-Mart´ınez, P. Botella-Rocamora, J. Pardo
Embedded Systems and Artificial Intelligence group
Departamento de ciencias f´ısicas, matem´aticas y de la computaci´on
Escuela Superior de Ense˜nanzas T´ecnicas (ESET)
Universidad CEU Cardenal Herrera, 46115 Alfara del Patriarca, Valencia (Spain)
ICANN – September 11, 2013

2. Time-series forecasting of indoor temperature using pre-trained Deep Neural Networks
Index
1 Introduction and motivation
2 Stacked Denoising Auto-Encoders
3 Time series forecasting
4 Experimentation
5 Conclusions and future work

3. Time-series forecasting of indoor temperature using pre-trained Deep Neural Networks
Introduction and motivation
Index
1 Introduction and motivation
2 Stacked Denoising Auto-Encoders
3 Time series forecasting
4 Experimentation
5 Conclusions and future work

4. Time-series forecasting of indoor temperature using pre-trained Deep Neural Networks
Introduction and motivation
Introduction and motivation
Time series forecasting: prediction future values given past data.
¯s = s0,...,si−1,si,si+1,...
Non-linear relationships could be found between the elements.
ANNs were widely used for this task, normally shallow models.
Deep architectures has been successful in computer vision,
speech signal processing, classification, . . .
Time series forecasting with deep architectures is starting to
receive interest (as far as we know, using Restricted Boltzmann
Machines).

5. Time-series forecasting of indoor temperature using pre-trained Deep Neural Networks
Introduction and motivation
Deep architectures on time series
Expectations
Time series are characterized by more or less complex
dependencies. For indoor temperature forecasting:
Known dependencies: time of the day, day of the year.
Hidden dependencies: number of people in a room.
Short-term dependencies and long-term dependencies.
Normally, expert knowledge is introduced to take into account
known dependencies; data preprocessing: detrend, deseasoned.
A deep model could learn some of these dependencies using
several layers.

6. Time-series forecasting of indoor temperature using pre-trained Deep Neural Networks
Introduction and motivation
Forecasting of indoor temperature with deep ANNs
What have we done in this work?
Evaluation of pre-training and denoising techniques in a time
series forecasting task.
Results: slightly better generalization, less over-fitting.
Problems: lack of data, not complex enough task.
15
16
17
18
19
20
21
22
23
24
25
26
0 2000 4000 6000 8000 10000
ºC
Time (minutes)

7. Time-series forecasting of indoor temperature using pre-trained Deep Neural Networks
Stacked Denoising Auto-Encoders
Index
1 Introduction and motivation
2 Stacked Denoising Auto-Encoders
3 Time series forecasting
4 Experimentation
5 Conclusions and future work

8. Time-series forecasting of indoor temperature using pre-trained Deep Neural Networks
Stacked Denoising Auto-Encoders
Stacked Denoising Auto-Encoders
A Denoising Auto-Encoder is a neural network which receives a
noisy input and produces its cleaned version.
Gaussian additive noise (σ): ˙x = x+N (0,σ2
I)
Masking noise (p): ˜x = MN(˙x) with p probability.
Encoding: h(˜x) = so ftsign(b+W ˜x)
Decoding (denoising): ˆx = g(h(˜x)) = so ftsign(c+WT
h(˜x))
˙x
h(˜x)
˜x ˆx
W WT
x
GN(x)
MN(˙x)
x is an input vector, h(·) is the hidden layer vector, b and c are bias
vectors, W is a weights matrix, softsign(·) =
x
1+|x|

9. Time-series forecasting of indoor temperature using pre-trained Deep Neural Networks
Stacked Denoising Auto-Encoders
Stacked Denoising Auto-Encoders
Greedy training building layer-by-layer auto-encoders.
Stack all the trained weights to produce the final result.
Stack a forecasting layer (linear activation).
Train the whole neural network.

10. Time-series forecasting of indoor temperature using pre-trained Deep Neural Networks
Time series forecasting
Index
1 Introduction and motivation
2 Stacked Denoising Auto-Encoders
3 Time series forecasting
4 Experimentation
5 Conclusions and future work

11. Time-series forecasting of indoor temperature using pre-trained Deep Neural Networks
Time series forecasting
Time series forecasting
Univariate vs multivariate.
Single-step-ahead vs multi-step-ahead.
Iterative forecasting vs direct forecasting.
Multiple Input One Output vs Multiple Input Multiple Output.
ˆst+H
t+1 = F(st
t−I+1)
MIMO modelling is natural in ANNs, because they take profit of the
input/output mapping.
F is a forecasting model, H the number of predicted samples, I the number of past
samples taken as input.

12. Time-series forecasting of indoor temperature using pre-trained Deep Neural Networks
Experimentation
Index
1 Introduction and motivation
2 Stacked Denoising Auto-Encoders
3 Time series forecasting
4 Experimentation
5 Conclusions and future work

13. Time-series forecasting of indoor temperature using pre-trained Deep Neural Networks
Experimentation
Dataset
Dataset
Captured during 2011, March
and June.
1 minute sampling period.
Reduced and smoothed by
computing mean every 15
samples.
Differences between adjacent
samples were computed to
remove the trend.
Partition # of samples # of days
Training 2016 21
Validation 672 7
Test 672 7

14. Time-series forecasting of indoor temperature using pre-trained Deep Neural Networks
Experimentation
Evaluation measures
Evaluation measures
Mean Absolute Error (MAE)
Root Mean Square Error (RMSE)
MAE (t) =
1
|D|
|D|
∑
t=I
1
H
H
∑
h=1
|ˆst+h −st+h|
RMSE (t) =
1
|D|
|D|
∑
t=I
1
H
H
∑
h=1
(ˆst+h −st+h)2
|D| is the size of the dataset, H the future horizon, ˆst+h the forecasted value, st+h the
ground truth.

15. Time-series forecasting of indoor temperature using pre-trained Deep Neural Networks
Experimentation
Experiments
Experiments
Different training modes comparison
TM-0 consists in a standard training of an ANN.
TM-1 pre-train the ANN using SDAE and fine-tuning of the whole
network
TM-2 pre-train the ANN using SDAE and fine-tuning of only last
layer (forecasting layer).

16. Time-series forecasting of indoor temperature using pre-trained Deep Neural Networks
Experimentation
Experiments
Experiments
Training description
Back-propagation with mini-batch size 32.
Mean Square Error (MSE) loss function.
Future horizon of 12 samples (three hours).
Minimum of 50 epochs, maximum of 4000.
Random search hyper-parameter optimization:
learning rate, momentum, weight decay,
number of hidden layers, hidden layer sizes,
number of inputs,
mask noise percentage.
3600 experiments for tuning.

17. Time-series forecasting of indoor temperature using pre-trained Deep Neural Networks
Experimentation
Results
Results
Best topologies
- TM-0: 60 — 756 — 60 — 12
- TM-1: 48 — 648 — 920 — 16 — 12
- TM-2: 96 — 712 — 12
TM-0 has convergence problems with deep networks:
33% of two layered network experiments do not converge.
58% of three layered network experiments do not converge.
Note that the topologies are not the same in the three cases, we took the best
topology for each training mode.

18. Time-series forecasting of indoor temperature using pre-trained Deep Neural Networks
Experimentation
Results
Results
20 random initializations of best hyper-parameters
0.115
0.120
0.125
0.130
0.135
0.140
TM-0 TM-1 TM-2
MAE*
Validation
Test
0.135
0.140
0.145
0.150
0.155
0.160
0.165
0.170
TM-0 TM-1 TM-2
RMSE*

19. Time-series forecasting of indoor temperature using pre-trained Deep Neural Networks
Experimentation
Results
Results
MSE of training partition during training
0.010
0.014
0.019
0.025
0.034
0.046
0.063
0.086
0.117
0.159
0 200 400 600 800 1000 1200 1400
TrainingMSE(log-scaled)
Epochs
TM-0
TM-1
TM-2

20. Time-series forecasting of indoor temperature using pre-trained Deep Neural Networks
Experimentation
Results
Results
MAE of test partition during training
0.117
0.159
0.216
0.293
0.398
0 200 400 600 800 1000 1200 1400
TestMAE*(log-scaled)
Epochs
best val TM-0
best val TM-1
best val TM-2
TM-0
TM-1
TM-2

21. Time-series forecasting of indoor temperature using pre-trained Deep Neural Networks
Conclusions and future work
Index
1 Introduction and motivation
2 Stacked Denoising Auto-Encoders
3 Time series forecasting
4 Experimentation
5 Conclusions and future work

22. Time-series forecasting of indoor temperature using pre-trained Deep Neural Networks
Conclusions and future work
Conclusions and future work
Pre-training, denoising techniques, and random hyper-parameter
optimization were used to carry out deep ANNs training in a
forecasting task.
Slightly better generalization performance at test set and a
reduction in over-fitting was observed (TM-1).
Fine-tuning phase of the whole deep model was needed to
ensure good results (TM-1 vs TM-2).
The short benefit of SDAE could be due to the low dimensionality
of the task.
In the future, this work will be extended by using larger
forecasting input window combined with multivariate forecasting.

23. Time-series forecasting of indoor temperature using pre-trained Deep Neural Networks
Conclusions and future work
Questions?
Thanks for your attention!

24. Time-series forecasting of indoor temperature using pre-trained Deep Neural Networks
Appendix
Appendix: Hyper-parameter optimization
Grid search part
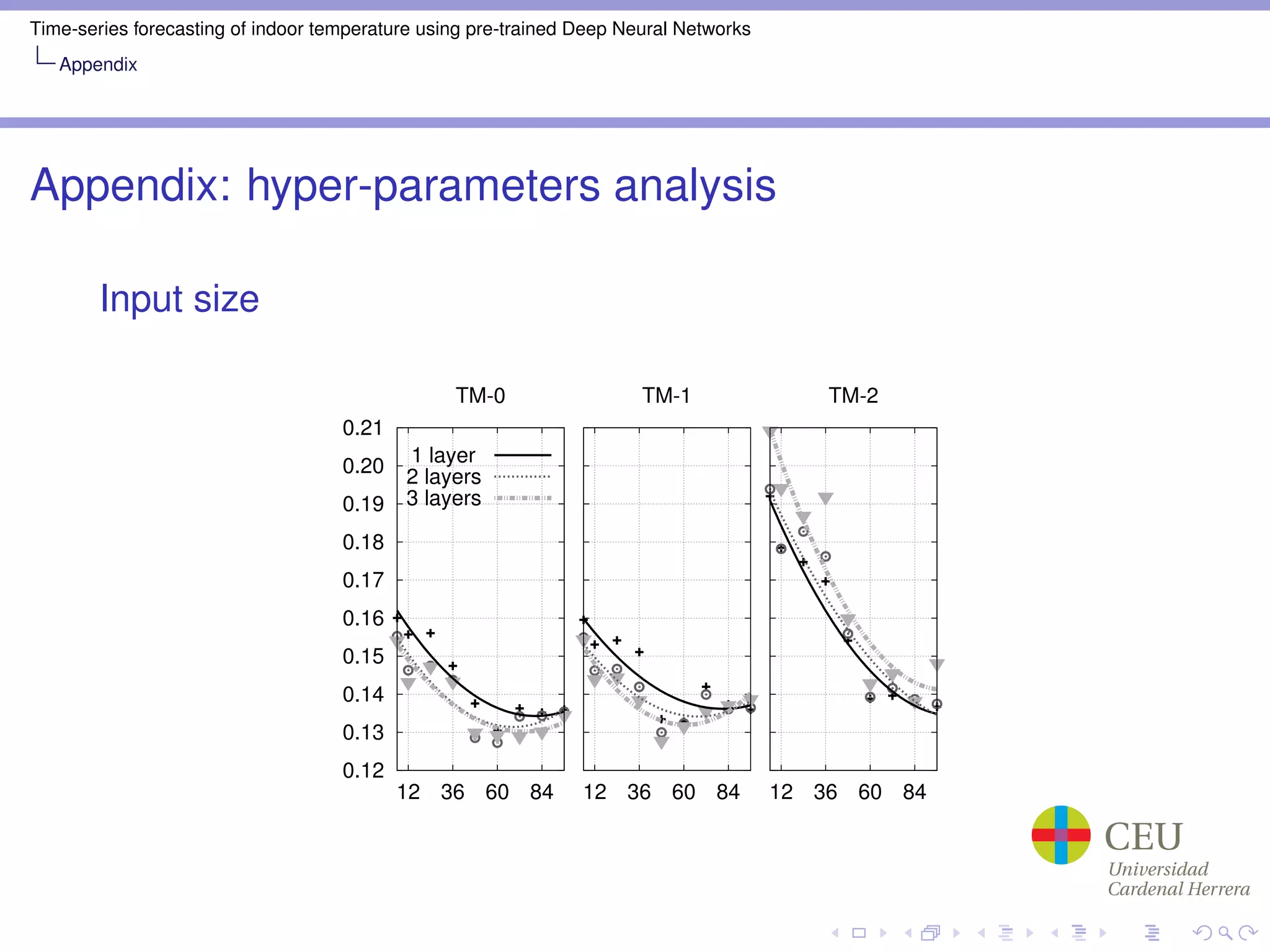
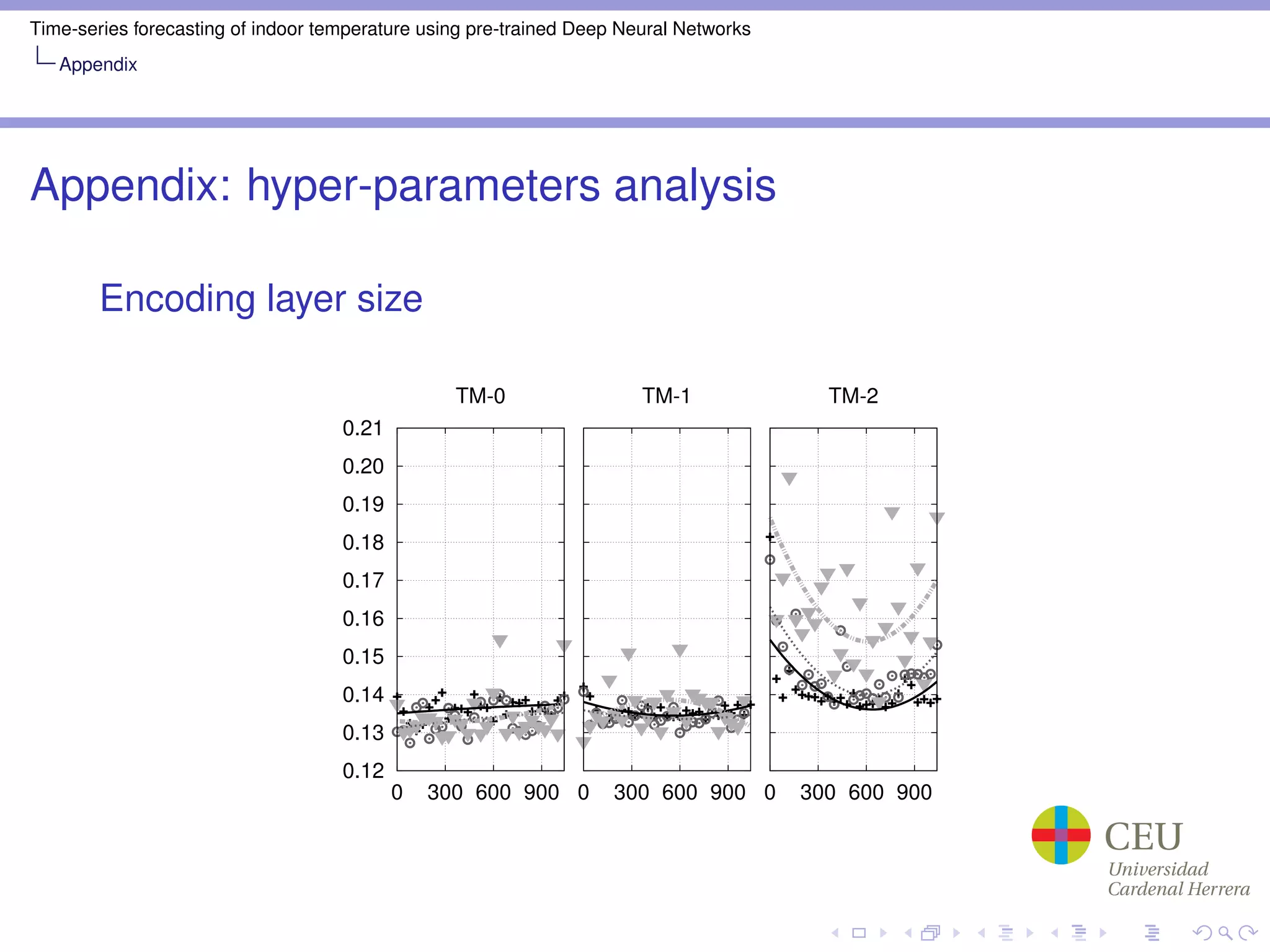
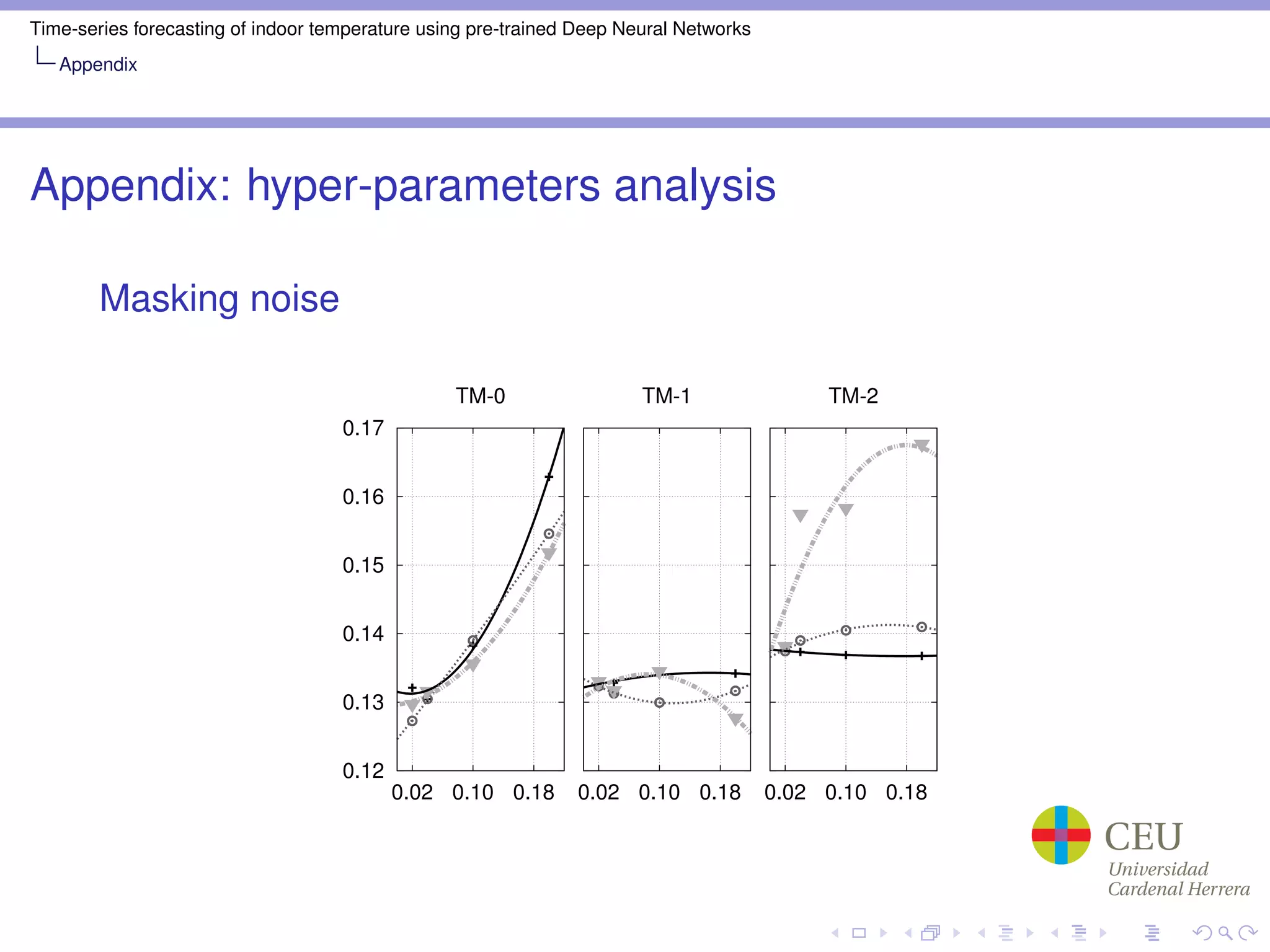
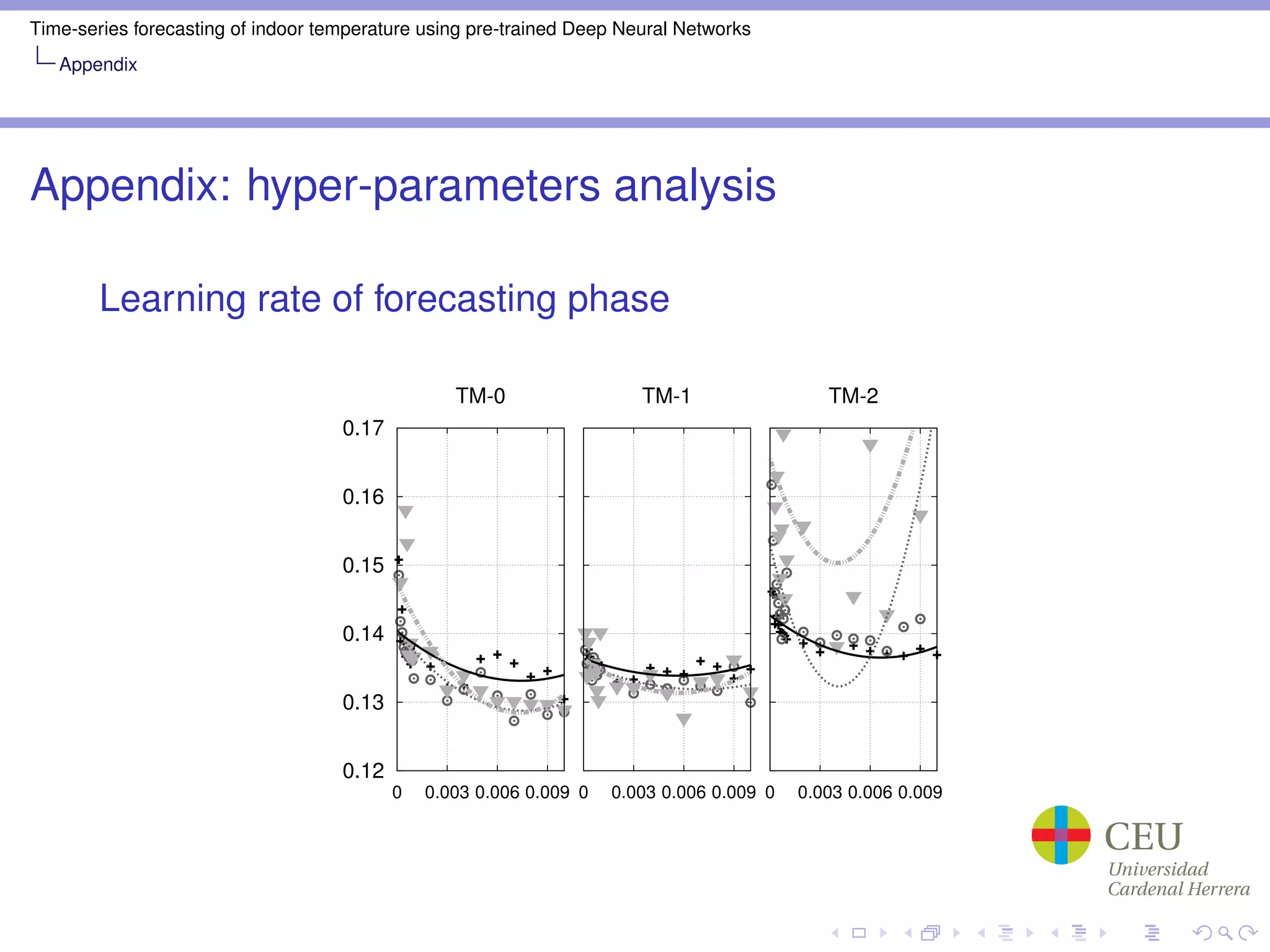
Train Mode: TM-0, TM-1, TM-2
Number of hidden layers: 1, 2, 3
Mask Noise: 0.02, 0.04, 0.10, 0.20
Random search part
100 random trials for every grid sweep
Input size: 12, 24, 36, 48, 60, 72, 84, 96
Learning rate: [10−3
,10−2
]
Momentum: ∼ N (10−3
,5×10−3
), ignoring negative values
Weight decay: [0,10−5
]
Hidden layer sizes: [4,1024]

25. Time-series forecasting of indoor temperature using pre-trained Deep Neural Networks
Appendix
Appendix: hyper-parameters analysis
Input size
0.12
0.13
0.14
0.15
0.16
0.17
0.18
0.19
0.20
0.21
12 36 60 84
TM-0
12 36 60 84
TM-1
1 layer
2 layers
3 layers
12 36 60 84
TM-2

26. Time-series forecasting of indoor temperature using pre-trained Deep Neural Networks
Appendix
Appendix: hyper-parameters analysis
Encoding layer size
0.12
0.13
0.14
0.15
0.16
0.17
0.18
0.19
0.20
0.21
0 300 600 900
TM-0
0 300 600 900
TM-1
0 300 600 900
TM-2

27. Time-series forecasting of indoor temperature using pre-trained Deep Neural Networks
Appendix
Appendix: hyper-parameters analysis
Masking noise
0.12
0.13
0.14
0.15
0.16
0.17
0.02 0.10 0.18
TM-0
0.02 0.10 0.18
TM-1
0.02 0.10 0.18
TM-2

28. Time-series forecasting of indoor temperature using pre-trained Deep Neural Networks
Appendix
Appendix: hyper-parameters analysis
Learning rate of forecasting phase
0.12
0.13
0.14
0.15
0.16
0.17
0 0.003 0.006 0.009
TM-0
0 0.003 0.006 0.009
TM-1
0 0.003 0.006 0.009
TM-2

29. Time-series forecasting of indoor temperature using pre-trained Deep Neural Networks
Appendix
Appendix: results table
MAE
Validation (µ±σ) Test (µ±σ)
ETS 0.3004 0.3254
TM-0 0.1289±0.0011 0.12482±0.0010
TM-1 0.1287±0.0033 0.1223±0.0033
TM-2 0.1374±0.0007 0.1279±0.0011
RMSE
Validation (µ±σ) Test (µ±σ)
ETS 0.3648 0.3930
TM-0 0.1563±0.0011 0.1511±0.0012
TM-1 0.1565±0.0040 0.1473±0.0039
TM-2 0.1663±0.0009 0.1538±0.0013