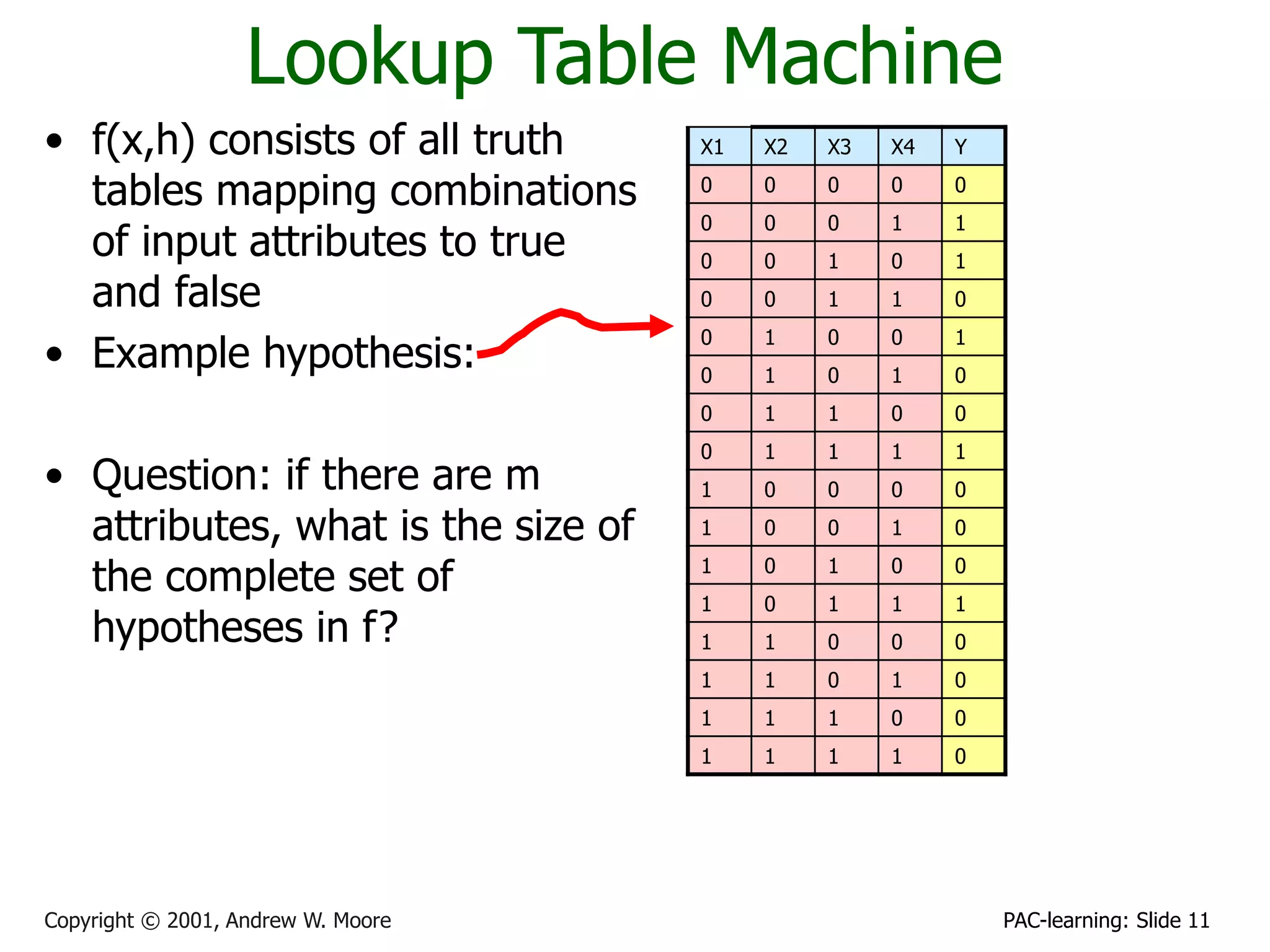
This document contains slides from a lecture on PAC (Probably Approximately Correct) learning given by Andrew W. Moore. The slides provide examples of different types of learning machines (classifiers) with different hypothesis spaces and calculate the number of training examples needed to PAC learn each machine to guarantee a low probability of error. For instance, it is shown that an AND-literals machine with m attributes has 3m possible hypotheses and the number of training examples needed to PAC learn is proportional to log(3m).

1. Nov 30th, 2001
Copyright © 2001, Andrew W. Moore
PAC-learning
Andrew W. Moore
Associate Professor
School of Computer Science
Carnegie Mellon University
www.cs.cmu.edu/~awm
awm@cs.cmu.edu
412-268-7599
Note to other teachers and users of these slides. Andrew would
be delighted if you found this source material useful in giving
your own lectures. Feel free to use these slides verbatim, or to
modify them to fit your own needs. PowerPoint originals are
available. If you make use of a significant portion of these slides
in your own lecture, please include this message, or the
following link to the source repository of Andrew’s tutorials:
http://www.cs.cmu.edu/~awm/tutorials . Comments and
corrections gratefully received.

2. PAC-learning: Slide 2
Copyright © 2001, Andrew W. Moore
Probably Approximately Correct
(PAC) Learning
• Imagine we’re doing classification with categorical
inputs.
• All inputs and outputs are binary.
• Data is noiseless.
• There’s a machine f(x,h) which has H possible
settings (a.k.a. hypotheses), called h1, h2 .. hH.

3. PAC-learning: Slide 3
Copyright © 2001, Andrew W. Moore
Example of a machine
• f(x,h) consists of all logical sentences about X1, X2
.. Xm that contain only logical ands.
• Example hypotheses:
• X1 ^ X3 ^ X19
• X3 ^ X18
• X7
• X1 ^ X2 ^ X2 ^ x4 … ^ Xm
• Question: if there are 3 attributes, what is the
complete set of hypotheses in f?

4. PAC-learning: Slide 4
Copyright © 2001, Andrew W. Moore
Example of a machine
• f(x,h) consists of all logical sentences about X1, X2
.. Xm that contain only logical ands.
• Example hypotheses:
• X1 ^ X3 ^ X19
• X3 ^ X18
• X7
• X1 ^ X2 ^ X2 ^ x4 … ^ Xm
• Question: if there are 3 attributes, what is the
complete set of hypotheses in f? (H = 8)
True X2 X3 X2 ^ X3
X1 X1 ^ X2 X1 ^ X3 X1 ^ X2 ^ X3

5. PAC-learning: Slide 5
Copyright © 2001, Andrew W. Moore
And-Positive-Literals Machine
• f(x,h) consists of all logical sentences about X1, X2
.. Xm that contain only logical ands.
• Example hypotheses:
• X1 ^ X3 ^ X19
• X3 ^ X18
• X7
• X1 ^ X2 ^ X2 ^ x4 … ^ Xm
• Question: if there are m attributes, how many
hypotheses in f?

6. PAC-learning: Slide 6
Copyright © 2001, Andrew W. Moore
And-Positive-Literals Machine
• f(x,h) consists of all logical sentences about X1, X2
.. Xm that contain only logical ands.
• Example hypotheses:
• X1 ^ X3 ^ X19
• X3 ^ X18
• X7
• X1 ^ X2 ^ X2 ^ x4 … ^ Xm
• Question: if there are m attributes, how many
hypotheses in f? (H = 2m)

7. PAC-learning: Slide 7
Copyright © 2001, Andrew W. Moore
And-Literals Machine
• f(x,h) consists of all logical
sentences about X1, X2 ..
Xm or their negations that
contain only logical ands.
• Example hypotheses:
• X1 ^ ~X3 ^ X19
• X3 ^ ~X18
• ~X7
• X1 ^ X2 ^ ~X3 ^ … ^ Xm
• Question: if there are 2
attributes, what is the
complete set of hypotheses
in f?

8. PAC-learning: Slide 8
Copyright © 2001, Andrew W. Moore
And-Literals Machine
• f(x,h) consists of all logical
sentences about X1, X2 ..
Xm or their negations that
contain only logical ands.
• Example hypotheses:
• X1 ^ ~X3 ^ X19
• X3 ^ ~X18
• ~X7
• X1 ^ X2 ^ ~X3 ^ … ^ Xm
• Question: if there are 2
attributes, what is the
complete set of hypotheses
in f? (H = 9)
True True
True X2
True ~X2
X1 True
X1 ^ X2
X1 ^ ~X2
~X1 True
~X1 ^ X2
~X1 ^ ~X2

9. PAC-learning: Slide 9
Copyright © 2001, Andrew W. Moore
And-Literals Machine
• f(x,h) consists of all logical
sentences about X1, X2 ..
Xm or their negations that
contain only logical ands.
• Example hypotheses:
• X1 ^ ~X3 ^ X19
• X3 ^ ~X18
• ~X7
• X1 ^ X2 ^ ~X3 ^ … ^ Xm
• Question: if there are m
attributes, what is the size of
the complete set of
hypotheses in f?
True True
True X2
True ~X2
X1 True
X1 ^ X2
X1 ^ ~X2
~X1 True
~X1 ^ X2
~X1 ^ ~X2

10. PAC-learning: Slide 10
Copyright © 2001, Andrew W. Moore
And-Literals Machine
• f(x,h) consists of all logical
sentences about X1, X2 ..
Xm or their negations that
contain only logical ands.
• Example hypotheses:
• X1 ^ ~X3 ^ X19
• X3 ^ ~X18
• ~X7
• X1 ^ X2 ^ ~X3 ^ … ^ Xm
• Question: if there are m
attributes, what is the size of
the complete set of
hypotheses in f? (H = 3m)
True True
True X2
True ~X2
X1 True
X1 ^ X2
X1 ^ ~X2
~X1 True
~X1 ^ X2
~X1 ^ ~X2

11. PAC-learning: Slide 11
Copyright © 2001, Andrew W. Moore
Lookup Table Machine
• f(x,h) consists of all truth
tables mapping combinations
of input attributes to true
and false
• Example hypothesis:
• Question: if there are m
attributes, what is the size of
the complete set of
hypotheses in f?
X1 X2 X3 X4 Y
0 0 0 0 0
0 0 0 1 1
0 0 1 0 1
0 0 1 1 0
0 1 0 0 1
0 1 0 1 0
0 1 1 0 0
0 1 1 1 1
1 0 0 0 0
1 0 0 1 0
1 0 1 0 0
1 0 1 1 1
1 1 0 0 0
1 1 0 1 0
1 1 1 0 0
1 1 1 1 0

12. PAC-learning: Slide 12
Copyright © 2001, Andrew W. Moore
Lookup Table Machine
• f(x,h) consists of all truth
tables mapping combinations
of input attributes to true
and false
• Example hypothesis:
• Question: if there are m
attributes, what is the size of
the complete set of
hypotheses in f?
X1 X2 X3 X4 Y
0 0 0 0 0
0 0 0 1 1
0 0 1 0 1
0 0 1 1 0
0 1 0 0 1
0 1 0 1 0
0 1 1 0 0
0 1 1 1 1
1 0 0 0 0
1 0 0 1 0
1 0 1 0 0
1 0 1 1 1
1 1 0 0 0
1 1 0 1 0
1 1 1 0 0
1 1 1 1 0
m
H 2
2


13. PAC-learning: Slide 13
Copyright © 2001, Andrew W. Moore
A Game
• We specify f, the machine
• Nature choose hidden random hypothesis h*
• Nature randomly generates R datapoints
•How is a datapoint generated?
1.Vector of inputs xk = (xk1,xk2, xkm) is
drawn from a fixed unknown distrib: D
2.The corresponding output yk=f(xk , h*)
• We learn an approximation of h* by choosing
some hest for which the training set error is 0

14. PAC-learning: Slide 14
Copyright © 2001, Andrew W. Moore
Test Error Rate
• We specify f, the machine
• Nature choose hidden random hypothesis h*
• Nature randomly generates R datapoints
•How is a datapoint generated?
1.Vector of inputs xk = (xk1,xk2, xkm) is
drawn from a fixed unknown distrib: D
2.The corresponding output yk=f(xk , h*)
• We learn an approximation of h* by choosing
some hest for which the training set error is 0
• For each hypothesis h ,
• Say h is Correctly Classified (CCd) if h has
zero training set error
• Define TESTERR(h )
= Fraction of test points that h will classify
correctly
= P(h classifies a random test point
correctly)
• Say h is BAD if TESTERR(h) > e

15. PAC-learning: Slide 15
Copyright © 2001, Andrew W. Moore
Test Error Rate
• We specify f, the machine
• Nature choose hidden random hypothesis h*
• Nature randomly generates R datapoints
•How is a datapoint generated?
1.Vector of inputs xk = (xk1,xk2, xkm) is
drawn from a fixed unknown distrib: D
2.The corresponding output yk=f(xk , h*)
• We learn an approximation of h* by choosing
some hest for which the training set error is 0
• For each hypothesis h ,
• Say h is Correctly Classified (CCd) if h has
zero training set error
• Define TESTERR(h )
= Fraction of test points that i will classify
correctly
= P(h classifies a random test point
correctly)
• Say h is BAD if TESTERR(h) > e
)
bad
is
|
)
,
(
Set,
Training
(
)
bad
is
|
CCd
is
(
h
y
h
x
f
k
P
h
h
P
k
k 



R
)
1
( e



16. PAC-learning: Slide 16
Copyright © 2001, Andrew W. Moore
Test Error Rate
• We specify f, the machine
• Nature choose hidden random hypothesis h*
• Nature randomly generates R datapoints
•How is a datapoint generated?
1.Vector of inputs xk = (xk1,xk2, xkm) is
drawn from a fixed unknown distrib: D
2.The corresponding output yk=f(xk , h*)
• We learn an approximation of h* by choosing
some hest for which the training set error is 0
• For each hypothesis h ,
• Say h is Correctly Classified (CCd) if h has
zero training set error
• Define TESTERR(h )
= Fraction of test points that i will classify
correctly
= P(h classifies a random test point
correctly)
• Say h is BAD if TESTERR(h) > e
)
bad
is
|
)
,
(
Set,
Training
(
)
bad
is
|
CCd
is
(
h
y
h
x
f
k
P
h
h
P
k
k 



R
)
1
( e



)
bad
a
learn
we
( h
P









h
h
P
bad
a
contains
s
'
CCd
of
set
the
 
 bad
is
^
CCd
is
. h
h
h
P

















bad)
is
^
CCd
is
(
:
bad)
is
^
CCd
is
(
bad)
is
^
CCd
is
(
2
2
1
1
H
H h
h
h
h
h
h
P
 


H
i
i
i h
h
P
1
bad
is
^
CCd
is
 


H
i
i
i h
h
P
1
bad
is
|
CCd
is
  R
i
i H
h
h
P
H )
1
(
bad
is
|
CCd
is e




17. PAC-learning: Slide 17
Copyright © 2001, Andrew W. Moore
PAC Learning
• Chose R such that with probability less than d we’ll
select a bad hest (i.e. an hest which makes mistakes
more than fraction e of the time)
• Probably Approximately Correct
• As we just saw, this can be achieved by choosing
R such that
• i.e. R such that
R
H
h
P )
1
(
)
bad
a
learn
we
( e
d 










d
e
1
log
log
69
.
0
2
2 H
R

18. PAC-learning: Slide 18
Copyright © 2001, Andrew W. Moore
PAC in action
Machine Example
Hypothesis
H R required to PAC-
learn
And-positive-
literals
X3 ^ X7 ^ X8 2m
And-literals X3 ^ ~X7 3m
Lookup Table
And-lits or
And-lits
(X1 ^ X5) v
(X2 ^ ~X7 ^ X8)
X1 X2 X3 X4 Y
0 0 0 0 0
0 0 0 1 1
0 0 1 0 1
0 0 1 1 0
0 1 0 0 1
0 1 0 1 0
0 1 1 0 0
0 1 1 1 1
1 0 0 0 0
1 0 0 1 0
1 0 1 0 0
1 0 1 1 1
1 1 0 0 0
1 1 0 1 0
1 1 1 0 0
1 1 1 1 0
m
2
2
m
m 2
2
3
)
3
( 







d
e
1
log
69
.
0
2
m







d
e
1
log
)
3
(log
69
.
0
2
2 m







d
e
1
log
2
69
.
0
2
m







d
e
1
log
)
3
log
2
(
69
.
0
2
2 m

19. PAC-learning: Slide 19
Copyright © 2001, Andrew W. Moore
PAC for decision trees of depth k
• Assume m attributes
• Hk = Number of decision trees of depth k
• H0 =2
• Hk+1 = (#choices of root attribute) *
(# possible left subtrees) *
(# possible right subtrees)
= m * Hk * Hk
• Write Lk = log2 Hk
• L0 = 1
• Lk+1 = log2 m + 2Lk
• So Lk = (2 k-1)(1+log2 m) +1
• So to PAC-learn, need











d
e
1
log
1
)
log
1
)(
1
2
(
69
.
0
2
2 m
R k

20. PAC-learning: Slide 20
Copyright © 2001, Andrew W. Moore
What you should know
• Be able to understand every step in the math that
gets you to
• Understand that you thus need this many records
to PAC-learn a machine with H hypotheses
• Understand examples of deducing H for various
machines
R
H
h
P )
1
(
)
bad
a
learn
we
( e
d 










d
e
1
log
log
69
.
0
2
2 H
R