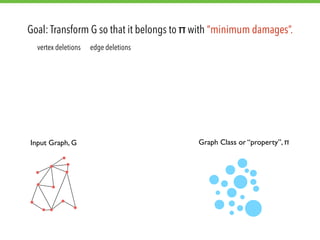
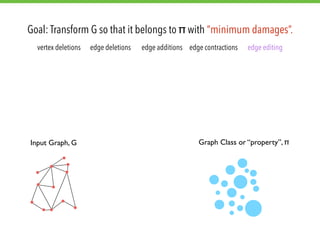
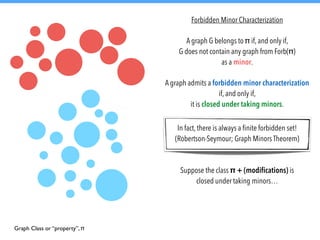
The document explores graph modification problems, focusing on the goal of transforming an input graph to belong to a specified class or property with minimal changes. It discusses various modification operations, such as vertex deletions and edge additions, and their implications on different graph classes and properties. Additionally, the document touches on algorithmic complexity and problem-solving approaches related to graph classification and modification.

1. Graph Modification
Problems
A Modern Perspective

3. Setting the stage: Definitions and Preliminary Observations

4. Setting the stage: Definitions and Preliminary Observations
Brief excursions into specific examples

5. Setting the stage: Definitions and Preliminary Observations
Brief excursions into specific examples
Current Trends & Future Directions

6. Ingredients of a typical Graph Modification Problem

8. Input Graph, G

9. Input Graph, G Graph Class or “property”, ᴨ

10. Goal: Transform G so that it belongs to ᴨ with “minimum damages”.
Input Graph, G Graph Class or “property”, ᴨ

11. Goal: Transform G so that it belongs to ᴨ with “minimum damages”.
Input Graph, G Graph Class or “property”, ᴨ

12. Goal: Transform G so that it belongs to ᴨ with “minimum damages”.
Input Graph, G Graph Class or “property”, ᴨ

13. Goal: Transform G so that it belongs to ᴨ with “minimum damages”.
vertex deletions
Input Graph, G Graph Class or “property”, ᴨ

14. Goal: Transform G so that it belongs to ᴨ with “minimum damages”.
vertex deletions edge deletions
Input Graph, G Graph Class or “property”, ᴨ

15. Goal: Transform G so that it belongs to ᴨ with “minimum damages”.
vertex deletions edge deletions edge additions
Input Graph, G Graph Class or “property”, ᴨ

16. Goal: Transform G so that it belongs to ᴨ with “minimum damages”.
vertex deletions edge deletions edge additions edge contractions
Input Graph, G Graph Class or “property”, ᴨ

17. Goal: Transform G so that it belongs to ᴨ with “minimum damages”.
vertex deletions edge deletions edge additions edge contractions edge editing
Input Graph, G Graph Class or “property”, ᴨ

18. Goal: Transform G so that it belongs to ᴨ with “minimum damages”.
vertex deletions edge deletions edge additions edge contractions edge editing
Input Graph, G
Vertex Cover
Edgeless Graphs

19. Goal: Transform G so that it belongs to ᴨ with “minimum damages”.
vertex deletions edge deletions edge additions edge contractions edge editing
Input Graph, G
Feedback Vertex Set
Acyclic Graphs

20. Goal: Transform G so that it belongs to ᴨ with “minimum damages”.
vertex deletions edge deletions edge additions edge contractions edge editing
Input Graph, G
Minimum Fill-In
Chordal Graphs

21. Goal: Transform G so that it belongs to ᴨ with “minimum damages”.
vertex deletions edge deletions edge additions edge contractions edge editing
Input Graph, G
Cluster Editing
Cluster Graphs

22. Goal: Transform G so that it belongs to ᴨ with “minimum damages”.

23. Goal: Transform G so that it belongs to ᴨ with “minimum damages”.
Minimum ᴨ-Completion

24. Goal: Transform G so that it belongs to ᴨ with “minimum damages”.
Minimum ᴨ-Completion Minimum ᴨ-Supergraph

25. Goal: Transform G so that it belongs to ᴨ with “minimum damages”.
Minimum ᴨ-Completion
Minimum ᴨ-Deletion
Minimum ᴨ-Supergraph

26. Goal: Transform G so that it belongs to ᴨ with “minimum damages”.
Minimum ᴨ-Completion
Minimum ᴨ-Deletion
Minimum ᴨ-Supergraph
Maximum ᴨ-Spanning Subgraph

27. Goal: Transform G so that it belongs to ᴨ with “minimum damages”.
Minimum ᴨ-Completion
Minimum ᴨ-Deletion
Minimum ᴨ-Editing
Minimum ᴨ-Supergraph
Maximum ᴨ-Spanning Subgraph

28. Goal: Transform G so that it belongs to ᴨ with “minimum damages”.
Minimum ᴨ-Completion
Minimum ᴨ-Deletion
Minimum ᴨ-Editing
Minimum ᴨ-Supergraph
Maximum ᴨ-Spanning Subgraph
Closest ᴨ-Graph

29. Goal: Transform G so that it belongs to ᴨ with “minimum damages”.
Minimum ᴨ-Completion
Minimum ᴨ-Deletion
Minimum ᴨ-Editing
Minimum ᴨ-Supergraph
Maximum ᴨ-Spanning Subgraph
Closest ᴨ-Graph
Minimum ᴨ-Vertex Deletion

30. Goal: Transform G so that it belongs to ᴨ with “minimum damages”.
Minimum ᴨ-Completion
Minimum ᴨ-Deletion
Minimum ᴨ-Editing
Minimum ᴨ-Supergraph
Maximum ᴨ-Spanning Subgraph
Closest ᴨ-Graph
Minimum ᴨ-Vertex Deletion Maximum ᴨ-Induced Subgraph

31. Goal: Transform G so that it belongs to ᴨ with “minimum damages”.
Minimum ᴨ-Completion
Minimum ᴨ-Deletion
Minimum ᴨ-Editing
Minimum ᴨ-Supergraph
Maximum ᴨ-Spanning Subgraph
Closest ᴨ-Graph
Minimum ᴨ-Vertex Deletion Maximum ᴨ-Induced Subgraph
Completion to Minimum Max-Clique

32. Goal: Transform G so that it belongs to ᴨ with “minimum damages”.
Minimum ᴨ-Completion
Minimum ᴨ-Deletion
Minimum ᴨ-Editing
Minimum ᴨ-Supergraph
Maximum ᴨ-Spanning Subgraph
Closest ᴨ-Graph
Minimum ᴨ-Vertex Deletion Maximum ᴨ-Induced Subgraph
Completion to Minimum Max-Clique
Modification with Restrictions, eg, the Sandwich problem

33. Goal: Transform G so that it belongs to ᴨ with “minimum damages”.
Minimum ᴨ-Completion
Minimum ᴨ-Deletion
Minimum ᴨ-Editing
Minimum ᴨ-Supergraph
Maximum ᴨ-Spanning Subgraph
Closest ᴨ-Graph
Minimum ᴨ-Vertex Deletion Maximum ᴨ-Induced Subgraph
Completion to Minimum Max-Clique
Modification with Restrictions, eg, the Sandwich problem
Restricted Classes of Input

34. Graph Class or “property”, ᴨ

35. Non-Trivial ᴨ admits infinitely many graphs, and also excludes infinitely many graphs.
Graph Class or “property”, ᴨ

36. Non-Trivial ᴨ admits infinitely many graphs, and also excludes infinitely many graphs.
Monotone If G belongs to ᴨ, then all subgraphs of G also belong to ᴨ.
Graph Class or “property”, ᴨ

37. Non-Trivial ᴨ admits infinitely many graphs, and also excludes infinitely many graphs.
Graph Class or “property”, ᴨ
Monotone
Hereditary
If G belongs to ᴨ, then all subgraphs of G also belong to ᴨ.
If G belongs to ᴨ, then all induced subgraphs of G also belong to ᴨ.

38. Non-Trivial ᴨ admits infinitely many graphs, and also excludes infinitely many graphs.
(Bipartite, Planar)
Graph Class or “property”, ᴨ
Monotone
Hereditary
If G belongs to ᴨ, then all subgraphs of G also belong to ᴨ.
If G belongs to ᴨ, then all induced subgraphs of G also belong to ᴨ.

39. Non-Trivial ᴨ admits infinitely many graphs, and also excludes infinitely many graphs.
(Bipartite, Planar)
Graph Class or “property”, ᴨ
Monotone
Hereditary
If G belongs to ᴨ, then all subgraphs of G also belong to ᴨ.
If G belongs to ᴨ, then all induced subgraphs of G also belong to ᴨ.
(Complete graphs, Forests)

40. Non-Trivial ᴨ admits infinitely many graphs, and also excludes infinitely many graphs.
(Bipartite, Planar)
Graph Class or “property”, ᴨ
Monotone
Hereditary
If G belongs to ᴨ, then all subgraphs of G also belong to ᴨ.
If G belongs to ᴨ, then all induced subgraphs of G also belong to ᴨ.
(Complete graphs, Forests)
Connectivity, Biconnectivity, Trees, Stars, Eulerian, etc.

42. Lewis &
Yannakakis
[1980]
The vertex-deletion problem is NP-complete for non-trivial,
hereditary properties.

43. Lewis &
Yannakakis
[1980]
The vertex-deletion problem is NP-complete for non-trivial,
hereditary properties.
Yannakakis
[1979]
The connected vertex-deletion problem is NP-complete for
non-trivial properties that hold on connected induced
subgraphs.

44. Lewis &
Yannakakis
[1980]
The vertex-deletion problem is NP-complete for non-trivial,
hereditary properties.
Yannakakis
[1979]
(Edgeless, Acyclic, etc.)
The connected vertex-deletion problem is NP-complete for
non-trivial properties that hold on connected induced
subgraphs.

45. Lewis &
Yannakakis
[1980]
The vertex-deletion problem is NP-complete for non-trivial,
hereditary properties.
Yannakakis
[1979]
(Edgeless, Acyclic, etc.)
The connected vertex-deletion problem is NP-complete for
non-trivial properties that hold on connected induced
subgraphs.(
Trees, Stars, etc.)

47. Edge-Deletion or Completion problems are sometimes easier than their
vertex-deletion counterparts.

48. Edge-Deletion or Completion problems are sometimes easier than their
vertex-deletion counterparts.
Add edges to make the input graph a cluster graph.

49. Edge-Deletion or Completion problems are sometimes easier than their
vertex-deletion counterparts.
Add edges to make the input graph a cluster graph.
Remove edges to make the input graph edgeless.

50. Edge-Deletion or Completion problems are sometimes easier than their
vertex-deletion counterparts.
Add edges to make the input graph a cluster graph.
Remove edges to make the input graph edgeless.
Remove edges to make the input graph acyclic.

51. Edge-Deletion or Completion problems are sometimes easier than their
vertex-deletion counterparts.
Add edges to make the input graph a cluster graph.
Remove edges to make the input graph edgeless.
Remove edges to make the input graph acyclic.
Remove edges to make the input graph bipartite.

52. Edge-Deletion or Completion problems are sometimes easier than their
vertex-deletion counterparts.
Add edges to make the input graph a cluster graph.
Remove edges to make the input graph edgeless.
Remove edges to make the input graph acyclic.

53. Edge-Deletion or Completion problems are sometimes easier than their
vertex-deletion counterparts.
Add edges to make the input graph a cluster graph.
Remove edges to make the input graph edgeless.
Remove edges to make the input graph acyclic.
Alon, Shapira
& Sudakov
[2009]
Given a property ᴨ such that ᴨ holds for every
bipartite graph, the Minimum ᴨ-Deletion problem is NP-hard.

54. Edge-Deletion or Completion problems are sometimes easier than their
vertex-deletion counterparts.
Add edges to make the input graph a cluster graph.
Remove edges to make the input graph edgeless.
Remove edges to make the input graph acyclic.
Alon, Shapira
& Sudakov
[2009]
Given a property ᴨ such that ᴨ holds for every
bipartite graph, the Minimum ᴨ-Deletion problem is NP-hard.
(Triangle-­free)

55. Edge-Deletion or Completion problems are sometimes easier than their
vertex-deletion counterparts.
Add edges to make the input graph a cluster graph.
Remove edges to make the input graph edgeless.
Remove edges to make the input graph acyclic.
Alon, Shapira
& Sudakov
[2009]
Given a property ᴨ such that ᴨ holds for every
bipartite graph, the Minimum ᴨ-Deletion problem is NP-hard.
Colbourn &
El-Mallah
[1988]
(Triangle-­free)
Making a graph Pk-free by deleting the minimum number of
edges is NP-hard for every k > 2.

56. edge editing
edge contractions
vertex deletions
edge additions
edge deletions
Graph Class or “property”, ᴨ

57. edge editing
edge contractions
vertex deletions
edge additions
edge deletions
Graph Class or “property”, ᴨ
Perfect
Trivially Perfect
Cographs
Permutation Graphs
Bipartite
Trees
Weakly Chordal
Chordal
Strongly Chordal
Split
Interval
Proper Interval
Unit Interval
Forests
Caterpillars
Chain
Chordal Bipartite
Distance Hereditary
Comparability
Trapezoid
CoChordal
Circle
Planar
k-Connected

58. Graph Modification
Problems
A Modern Perspective

59. Graph Modification
Problems
Why bother?

61. Special Graph Classes — correspond to some desirable property in real-world data.

62. Special Graph Classes — correspond to some desirable property in real-world data.
Planar Graphs
Interval Graphs
Cluster Graphs
k-Connected Graphs
Directed Acyclic Graphs
Chordal Graphs

63. Special Graph Classes — correspond to some desirable property in real-world data.
Planar Graphs
Interval Graphs
Cluster Graphs
k-Connected Graphs
Directed Acyclic Graphs
Chordal Graphs
Graph Drawing
Physical Mapping of DNA
Correlation Clustering
Reliability of Networks
Deadlock Recovery, Operating Systems
Gaussian Elimination over Sparse Matrices

64. Special Graph Classes — correspond to some desirable property in real-world data.
We would like to “achieve” these properties with minimum cost, which
naturally leads us to the graph modification framework.
Planar Graphs
Interval Graphs
Cluster Graphs
k-Connected Graphs
Directed Acyclic Graphs
Chordal Graphs
Graph Drawing
Physical Mapping of DNA
Correlation Clustering
Reliability of Networks
Deadlock Recovery, Operating Systems
Gaussian Elimination over Sparse Matrices

65. Graph Modification
Problems
Algorithms

66. Graph Class or “property”, ᴨ

67. Graph Class or “property”, ᴨ
Forbidden Subgraph Characterization
A graph G belongs to ᴨ if, and only if,
G does not contain any graph from Forb(ᴨ)
as an induced subgraph.

68. Graph Class or “property”, ᴨ
Forbidden Subgraph Characterization
A graph G belongs to ᴨ if, and only if,
G does not contain any graph from Forb(ᴨ)
as an induced subgraph.
Forbidden Minor Characterization
A graph G belongs to ᴨ if, and only if,
G does not contain any graph from Forb(ᴨ)
as a minor.

69. Graph Class or “property”, ᴨ
Forbidden Subgraph Characterization
A graph admits a forbidden subgraph characterization
if, and only if,
it is closed under taking induced subgraphs (hereditary),
that is, the property is preserved under vertex deletions.
Forbidden Minor Characterization
A graph G belongs to ᴨ if, and only if,
G does not contain any graph from Forb(ᴨ)
as a minor.

70. Graph Class or “property”, ᴨ
Forbidden Subgraph Characterization
A graph admits a forbidden subgraph characterization
if, and only if,
it is closed under taking induced subgraphs (hereditary),
that is, the property is preserved under vertex deletions.
Forbidden Minor Characterization
A graph admits a forbidden minor characterization
if, and only if,
it is closed under taking minors,
that is, the property is preserved under vertex deletions,
edge deletions and edge contractions.

71. Graph Class or “property”, ᴨ
Forbidden Subgraph Characterization
A graph admits a forbidden subgraph characterization
if, and only if,
it is closed under taking induced subgraphs (hereditary),
that is, the property is preserved under vertex deletions.
Forbidden Minor Characterization
A graph admits a forbidden minor characterization
if, and only if,
it is closed under taking minors,
that is, the property is preserved under vertex deletions,
edge deletions and edge contractions.

72. Graph Class or “property”, ᴨ
Forbidden Subgraph Characterization
A graph admits a forbidden subgraph characterization
if, and only if,
it is closed under taking induced subgraphs (hereditary),
that is, the property is preserved under vertex deletions.
If there are finitely many forbidden graphs,
then the corresponding graph modification problem is FPT.
Forbidden Minor Characterization
A graph admits a forbidden minor characterization
if, and only if,
it is closed under taking minors,
that is, the property is preserved under vertex deletions,
edge deletions and edge contractions.

73. Graph Class or “property”, ᴨ
Forbidden Subgraph Characterization
A graph admits a forbidden subgraph characterization
if, and only if,
it is closed under taking induced subgraphs (hereditary),
that is, the property is preserved under vertex deletions.
If there are finitely many forbidden graphs,
then the corresponding graph modification problem is FPT.
Forbidden Minor Characterization
A graph admits a forbidden minor characterization
if, and only if,
it is closed under taking minors,
that is, the property is preserved under vertex deletions,
edge deletions and edge contractions.
If there are finitely many forbidden minors…?

74. Graph Class or “property”, ᴨ
Forbidden Minor Characterization
A graph G belongs to ᴨ if, and only if,
G does not contain any graph from Forb(ᴨ)
as a minor.
A graph admits a forbidden minor characterization
if, and only if,
it is closed under taking minors.

75. Graph Class or “property”, ᴨ
Forbidden Minor Characterization
A graph G belongs to ᴨ if, and only if,
G does not contain any graph from Forb(ᴨ)
as a minor.
A graph admits a forbidden minor characterization
if, and only if,
it is closed under taking minors.
In fact, there is always a finite forbidden set!
(Robertson-Seymour; Graph Minors Theorem)

76. Graph Class or “property”, ᴨ
Forbidden Minor Characterization
A graph G belongs to ᴨ if, and only if,
G does not contain any graph from Forb(ᴨ)
as a minor.
A graph admits a forbidden minor characterization
if, and only if,
it is closed under taking minors.
In fact, there is always a finite forbidden set!
(Robertson-Seymour; Graph Minors Theorem)
Suppose the class ᴨ + (modifications) is
closed under taking minors…

77. Graph Class or “property”, ᴨ
Forbidden Minor Characterization
A graph G belongs to ᴨ if, and only if,
G does not contain any graph from Forb(ᴨ)
as a minor.
A graph admits a forbidden minor characterization
if, and only if,
it is closed under taking minors.
In fact, there is always a finite forbidden set!
(Robertson-Seymour; Graph Minors Theorem)
Suppose the class ᴨ + (modifications) is
closed under taking minors…
+ (modifications)

78. Graph Class or “property”, ᴨ
Forbidden Minor Characterization
A graph G belongs to ᴨ if, and only if,
G does not contain any graph from Forb(ᴨ)
as a minor.
A graph admits a forbidden minor characterization
if, and only if,
it is closed under taking minors.
In fact, there is always a finite forbidden set!
(Robertson-Seymour; Graph Minors Theorem)
Suppose the class ᴨ + (modifications) is
closed under taking minors…
Now: the graph modification problem has boiled down
to a membership testing problem, which can be
done in cubic time, given the finite forbidden set.
+ (modifications)

79. Forbidden Subgraph Characterization
A graph admits a forbidden subgraph characterization
if, and only if,
it is closed under taking induced subgraphs (hereditary),
that is, the property is preserved under vertex deletions.
Forbidden Minor Characterization
A graph admits a forbidden minor characterization
if, and only if,
it is closed under taking minors,
that is, the property is preserved under vertex deletions,
edge deletions and edge contractions.

80. Forbidden Subgraph Characterization
A graph admits a forbidden subgraph characterization
if, and only if,
it is closed under taking induced subgraphs (hereditary),
that is, the property is preserved under vertex deletions.
Can the node deletion question for hereditary properties
always be answered with the “graph minors hammer”?
Forbidden Minor Characterization
A graph admits a forbidden minor characterization
if, and only if,
it is closed under taking minors,
that is, the property is preserved under vertex deletions,
edge deletions and edge contractions.

81. Consider the property ᴨ of being wheel-free, that is,
not having any wheel as an induced subgraph.

82. Consider the property ᴨ of being wheel-free, that is,
not having any wheel as an induced subgraph.
The property is hereditary, but not minor-closed.

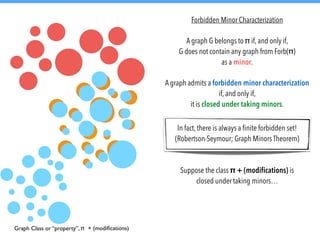
83. Consider the property ᴨ of being wheel-free, that is,
not having any wheel as an induced subgraph.
Wheel-Free Deletion and Wheel-Free Vertex Deletion
are W[2]-hard.
Lokshtanov
(2008)

84. Finding large induced subgraphs with property ᴨ.
Khot and Raman, (2002)

85. Finding large induced subgraphs with property ᴨ.
Khot and Raman, (2002)
If ᴨ is a hereditary property that contains all independent sets and all cliques,
or if ᴨ excludes some independent sets and some cliques,
then the problem of finding an induced subgraph of size at least k, satisfying ᴨ,
is FPT.

86. Finding large induced subgraphs with property ᴨ.
Khot and Raman, (2002)
If ᴨ is a hereditary property that contains all independent sets and all cliques,
or if ᴨ excludes some independent sets and some cliques,
then the problem of finding an induced subgraph of size at least k, satisfying ᴨ,
is FPT.
If ᴨ is a hereditary property contains all independent sets but not all cliques
(or vice versa),
then the problem of finding an induced subgraph of size at least k, satisfying ᴨ,
is W[1]-hard.

87. Finding large induced subgraphs with property ᴨ.
Khot and Raman, (2002)
If ᴨ is a hereditary property that contains all independent sets and all cliques,
or if ᴨ excludes some independent sets and some cliques,
then the problem of finding an induced subgraph of size at least k, satisfying ᴨ,
is FPT.
If ᴨ is a hereditary property contains all independent sets but not all cliques
(or vice versa),
then the problem of finding an induced subgraph of size at least k, satisfying ᴨ,
is W[1]-hard.
Ramsey Numbers!
Reduction from Independent Set

88. Vertex Cover
Can G be made edgeless by the removal of at most k vertices?
A simple randomized algorithm with an error probability of 2-k.

89. Vertex Cover
Can G be made edgeless by the removal of at most k vertices?
A simple randomized algorithm with an error probability of 2-k.

90. Vertex Cover
Can G be made edgeless by the removal of at most k vertices?
A simple randomized algorithm with an error probability of 2-k.

91. Feedback Vertex Set
Can G be made acyclic by the removal of at most k vertices?

92. Feedback Vertex Set
Can G be made acyclic by the removal of at most k vertices?

93. Feedback Vertex Set
Can G be made acyclic by the removal of at most k vertices?

94. Feedback Vertex Set
Can G be made acyclic by the removal of at most k vertices?

95. Feedback Vertex Set
Can G be made acyclic by the removal of at most k vertices?

96. Feedback Vertex Set
Can G be made acyclic by the removal of at most k vertices?
Let’s stare at the structure of a YES-instance.
#whisper: Let us also restrict ourselves to graphs of constant maximum degree, say five.

97. the k vertices corresponding to the FVS
(n-k) vertices and at most (n-k-1) edges “outside”.

98. the k vertices corresponding to the FVS
(n-k) vertices and at most (n-k-1) edges “outside”.

101. t “points of contact” between S and GS…

102. t “points of contact” between S and GS… at least t edges going across the two sets.

103. t “points of contact” between S and GS… at least t edges going across the two sets.
Delete the points of contact in GS to get at most 5t “pieces”.

104. t “points of contact” between S and GS… at least t edges going across the two sets.
Delete the points of contact in GS to get at most 5t “pieces”.
Suppose each piece has constant size, say c.

105. t “points of contact” between S and GS… at least t edges going across the two sets.
Delete the points of contact in GS to get at most 5t “pieces”.
Suppose each piece has constant size, say c.
The total number of edges in GS is at most 5ct.

106. t “points of contact” between S and GS… at least t edges going across the two sets.
Delete the points of contact in GS to get at most 5t “pieces”.
Suppose each piece has constant size, say c.
The total number of edges in GS is at most 5ct.
The number of good edges is at least t, and the number of bad edges is at most 5ct.

107. t “points of contact” between S and GS… at least t edges going across the two sets.
Delete the points of contact in GS to get at most 5t “pieces”.
Suppose each piece has constant size, say c.
The total number of edges in GS is at most 5ct.
The number of good edges is at least t, and the number of bad edges is at most 5ct.
In this scenario, a randomly chosen edge will be good with constant probability!

108. Bad scenario: one of the pieces is large.

109. These pieces have simple structure and bounded interaction with the outer world.

110. These pieces have simple structure and bounded interaction with the outer world.
Such pieces are called “protrusions”.

111. A Boundary of Constant Size
Constant Treewidth

112. A Boundary of Constant Size
Constant Treewidth

113. A Boundary of Constant Size
Constant Treewidth

117. The space of t-boundaried graphs
can be broken up into equivalence classes
based on how they “behave” with
the “other side” of the boundary.

120. The value of the
optimal solution
is the same
up to a constant.

121. The space of t-boundaried graphs
can be broken up into equivalence classes
based on how they “behave” with
the “other side” of the boundary.

122. The space of t-boundaried graphs
can be broken up into equivalence classes
based on how they “behave” with
the “other side” of the boundary.
For some problems,
the number of equivalence classes is finite,
allowing us to replace protrusions in graphs.

124. Finding protrusions? What do we replace them with?

125. The 퓕-Deletion Problem

126. The 퓕-Deletion Problem
Can G be made H-minor free, for all H in퓕,
by the removal of at most k vertices?

127. The 퓕-Deletion Problem
Can G be made H-minor free, for all H in퓕,
by the removal of at most k vertices?
Suppose G is a YES-instance, and further, suppose퓕contains at least one planar graph.

128. The 퓕-Deletion Problem
Can G be made H-minor free, for all H in퓕,
by the removal of at most k vertices?
Suppose G is a YES-instance, and further, suppose퓕contains at least one planar graph.
Then GS cannot have large grids.

129. The 퓕-Deletion Problem
Can G be made H-minor free, for all H in퓕,
by the removal of at most k vertices?
Suppose G is a YES-instance, and further, suppose퓕contains at least one planar graph.
Then GS cannot have large grids.
Thus the treewidth of GS is bounded by a constant that depends only on퓕.

130. The 퓕-Deletion Problem
Can G be made H-minor free, for all H in퓕,
by the removal of at most k vertices?
Suppose G is a YES-instance, and further, suppose퓕contains at least one planar graph.
Then GS cannot have large grids.
Thus the treewidth of GS is bounded by a constant that depends only on퓕.
The Planar 퓕-Deletion Problem

131. The Planar 퓕-Deletion Problem

132. The Planar 퓕-Deletion Problem
Ensure that protrusions are removed.

133. The Planar 퓕-Deletion Problem
Ensure that protrusions are removed.
Pick an edge uniformly at random.

134. The Planar 퓕-Deletion Problem
Ensure that protrusions are removed.
Pick an edge uniformly at random.
Include both endpoints.

135. The Planar 퓕-Deletion Problem
Ensure that protrusions are removed.
Pick an edge uniformly at random.
Include both endpoints. Pick an endpoint u.a.r.

136. The Planar 퓕-Deletion Problem
Ensure that protrusions are removed.
Pick an edge uniformly at random.
Include both endpoints. Pick an endpoint u.a.r.
Repeat till G is퓕-free.

137. The Planar 퓕-Deletion Problem
Ensure that protrusions are removed.
Pick an edge uniformly at random.
Include both endpoints. Pick an endpoint u.a.r.
(Approximation algorithm.)
Repeat till G is퓕-free.

138. The Planar 퓕-Deletion Problem
Ensure that protrusions are removed.
Pick an edge uniformly at random.
Include both endpoints. Pick an endpoint u.a.r.
(Approximation algorithm.) (Randomized algorithm.)
Repeat till G is퓕-free.

139. The Planar 퓕-Deletion Problem
accounts for several specific problems…

140. The Planar 퓕-Deletion Problem
accounts for several specific problems…
퓕
K2
K3
((k+1)-by-(k+1)) Grids
K2,3, K4
K4
K3,T2
Vertex Cover
Feedback Vertex Set
Treewidth k
Outerplanar
Series-Parallel
Pathwidth-One

142. Thanks to Graph Minors, we have a f(k)n2 algorithm for the 퓕-Deletion problem.

143. Thanks to Graph Minors, we have a f(k)n2 algorithm for the 퓕-Deletion problem.
For Planar 퓕-Deletion, the starting point was a double-exponential algorithm.
[Bodlaender, 1997]

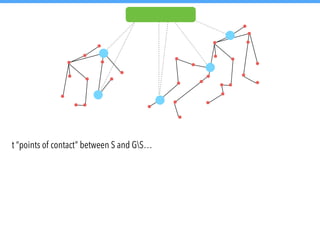
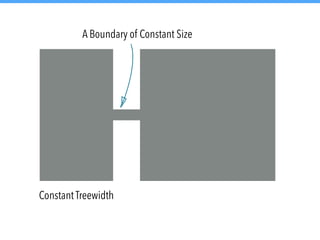
144. Thanks to Graph Minors, we have a f(k)n2 algorithm for the 퓕-Deletion problem.
For Planar 퓕-Deletion, the starting point was a double-exponential algorithm.
[Bodlaender, 1997]
Many single-exponential algorithms are known for special cases of 퓕.

145. Thanks to Graph Minors, we have a f(k)n2 algorithm for the 퓕-Deletion problem.
For Planar 퓕-Deletion, the starting point was a double-exponential algorithm.
[Bodlaender, 1997]
Many single-exponential algorithms are known for special cases of 퓕.
Feedback Vertex Set has Cao, Chen & Liu a O*(3.83k) algorithm.
[2010]

146. Thanks to Graph Minors, we have a f(k)n2 algorithm for the 퓕-Deletion problem.
For Planar 퓕-Deletion, the starting point was a double-exponential algorithm.
[Bodlaender, 1997]
Many single-exponential algorithms are known for special cases of 퓕.
Cao, Chen & Liu Feedback Vertex Set has a O*(3.83k) algorithm.
[2010]
{K4}-Deletion has Kim, Paul & Philip a O*(2O(k)) algorithm.
[2012]

147. Thanks to Graph Minors, we have a f(k)n2 algorithm for the 퓕-Deletion problem.
For Planar 퓕-Deletion, the starting point was a double-exponential algorithm.
[Bodlaender, 1997]
Many single-exponential algorithms are known for special cases of 퓕.
Cao, Chen & Liu Feedback Vertex Set has a O*(3.83k) algorithm.
[2010]
{K4}-Deletion has Kim, Paul & Philip a O*(2O(k)) algorithm.
Pathwidth-1-Deletion has a O*(4.65k) algorithm.
[2012]
Cygan, Pilipczuk,
Pilipczuk & Wojtaszczyk
[2010]

149. Fomin, Lokshtanov,
M. & Saurabh
[2013]
Planar퓕-Deletion admits a randomized (2O(k)n) algorithm
when every graph in퓕is connected.

150. Fomin, Lokshtanov,
M. & Saurabh
[2013]
Planar퓕-Deletion admits a randomized (2O(k)n) algorithm
when every graph in퓕is connected.
Best possible under ETH.

151. Fomin, Lokshtanov,
M. & Saurabh
[2013]
Planar퓕-Deletion admits a randomized (2O(k)n) algorithm
when every graph in퓕is connected.
Best possible under ETH.
Planar 퓕-Deletion admits a deterministic (2O(k)n log2n) algorithm
when every graph in 퓕 is connected.

152. Fomin, Lokshtanov,
M. & Saurabh
[2013]
Planar퓕-Deletion admits a randomized (2O(k)n) algorithm
when every graph in퓕is connected.
Best possible under ETH.
Planar 퓕-Deletion admits a deterministic (2O(k)n log2n) algorithm
when every graph in 퓕 is connected.
Planar퓕-Deletion admits an O(nm) randomized algorithm
that leads us to a constant-factor approximation.
Can we get a deterministic
constant-­factor approximation algorithm?

153. Fomin, Lokshtanov,
M. & Saurabh
[2013]
Planar퓕-Deletion admits a randomized (2O(k)n) algorithm
when every graph in퓕is connected.
Best possible under ETH.
Planar 퓕-Deletion admits a deterministic (2O(k)n log2n) algorithm
when every graph in 퓕 is connected.
Planar퓕-Deletion admits an O(nm) randomized algorithm
that leads us to a constant-factor approximation.
Can we get a deterministic
constant-­factor approximation algorithm?
Planar퓕-Deletion admits an deterministic algorithm
that leads us to a O(log3/2(OPT)) approximation.
Fomin, Lokshtanov,
M., Philip & Saurabh
[2013]

154. Fomin, Lokshtanov,
M. & Saurabh
[2013]
Planar퓕-Deletion admits a randomized (2O(k)n) algorithm
when every graph in퓕is connected.
Best possible under ETH.
Planar 퓕-Deletion admits a deterministic (2O(k)n log2n) algorithm
when every graph in 퓕 is connected.
Planar퓕-Deletion admits an O(nm) randomized algorithm
that leads us to a constant-factor approximation.
Can we get a deterministic
constant-­factor approximation algorithm?
Planar퓕-Deletion admits an deterministic algorithm
that leads us to a O(log3/2(OPT)) approximation.
Fomin, Lokshtanov,
M., Philip & Saurabh
[2013]
Kim, Langer, Paul, Reidl,
Rossmanith, Sau, & Sikdar
[2013]
Planar퓕-Deletion admits a deterministic (2O(k)n2) algorithm.

155. Fomin, Lokshtanov,
M. & Saurabh
[2013]
Planar퓕-Deletion admits a randomized (2O(k)n) algorithm
when every graph in퓕is connected.
Best possible under ETH.
Planar 퓕-Deletion admits a deterministic (2O(k)n) algorithm
when every graph in 퓕 is connected.
Planar퓕-Deletion admits an O(nm) randomized algorithm
that leads us to a constant-factor approximation.
Can we get a deterministic
constant-­factor approximation algorithm?
Planar퓕-Deletion admits an deterministic algorithm
that leads us to a O(log3/2(OPT)) approximation.
Fomin, Lokshtanov,
M., Philip & Saurabh
[2013]
Kim, Langer, Paul, Reidl,
Rossmanith, Sau, & Sikdar
[2013]
Planar퓕-Deletion admits a deterministic (2O(k)n2) algorithm.
Fomin, Lokshtanov,
M., Ramanujan& Saurabh
[2015]

157. Many polynomial kernels are also known for special cases of 퓕.

158. Many polynomial kernels are also known for special cases of 퓕.
Feedback Vertex Set has a Thomasse O(k2) instance kernel.
[2009]

159. Many polynomial kernels are also known for special cases of 퓕.
Thomasse Feedback Vertex Set has a O(k2) instance kernel.
[2009]
Vertex Cover has (Various) a O(k) vertex kernel.

160. Many polynomial kernels are also known for special cases of 퓕.
Thomasse Feedback Vertex Set has a O(k2) instance kernel.
[2009]
Vertex Cover has (Various) a O(k) vertex kernel.
Pathwidth-1-Deletion has a polynomial kernel
Cygan, Pilipczuk,
Pilipczuk & Wojtaszczyk
[2010]

161. Many polynomial kernels are also known for special cases of 퓕.
Thomasse Feedback Vertex Set has a O(k2) instance kernel.
[2009]
Vertex Cover has (Various) a O(k) vertex kernel.
Pathwidth-1-Deletion has a polynomial kernel
Cygan, Pilipczuk,
Pilipczuk & Wojtaszczyk
[2010]
Fomin, Lokshtanov,
M. & Saurabh
[2013]
Planar 퓕-Deletion admits a polynomial kernel.

162. Many polynomial kernels are also known for special cases of 퓕.
Thomasse Feedback Vertex Set has a O(k2) instance kernel.
[2009]
Vertex Cover has (Various) a O(k) vertex kernel.
Pathwidth-1-Deletion has a polynomial kernel
Cygan, Pilipczuk,
Pilipczuk & Wojtaszczyk
[2010]
Fomin, Lokshtanov,
M. & Saurabh
[2013]
Planar 퓕-Deletion admits a polynomial kernel.
Best possible under standard assumptions.

163. The 퓕-Deletion Problem

164. The 퓕-Deletion Problem
Very little is known beyond the graph minors result.

165. The 퓕-Deletion Problem
Very little is known beyond the graph minors result.
The most fundamental 퓕-deletion problem that is not accounted for by
Planar 퓕-Deletion is Planarization.

166. The 퓕-Deletion Problem
Very little is known beyond the graph minors result.
The most fundamental 퓕-deletion problem that is not accounted for by
Planar 퓕-Deletion is Planarization.
Marx and Schlotter
[2012]
Planarization admits an algorithm with running time
O(2g(k)n2) where g(k) = kO(k3)

167. The 퓕-Deletion Problem
Very little is known beyond the graph minors result.
The most fundamental 퓕-deletion problem that is not accounted for by
Planar 퓕-Deletion is Planarization.
Marx and Schlotter
[2012]
Planarization admits an algorithm with running time
O(2g(k)n2) where g(k) = kO(k3)
Kawarabayashi
[2009]
Planarization admits an algorithm with running time
O(f(k)n) where f(k) is not explicitly specified.

168. The 퓕-Deletion Problem
Very little is known beyond the graph minors result.
The most fundamental 퓕-deletion problem that is not accounted for by
Planar 퓕-Deletion is Planarization.
Marx and Schlotter
[2012]
Planarization admits an algorithm with running time
O(2g(k)n2) where g(k) = kO(k3)
Kawarabayashi
[2009]
Planarization admits an algorithm with running time
O(f(k)n) where f(k) is not explicitly specified.
Jansen, Lokshtanov &
Saurabh
[2014]
Planarization admits an algorithm with running time
2O(k log k)n, achieving the best combined dependence on k and n.

169. The 퓕-Deletion Problem
Very little is known beyond the graph minors result.
The most fundamental 퓕-deletion problem that is not accounted for by
Planar 퓕-Deletion is Planarization.
The question of kernels is completely open.
Marx and Schlotter
[2012]
Planarization admits an algorithm with running time
O(2g(k)n2) where g(k) = kO(k3)
Kawarabayashi
[2009]
Planarization admits an algorithm with running time
O(f(k)n) where f(k) is not explicitly specified.
Jansen, Lokshtanov &
Saurabh
[2014]
Planarization admits an algorithm with running time
2O(k log k)n, achieving the best combined dependence on k and n.

170. Graph Modification
Problems
When the operation induces hardness

171. Contraction Problems

172. Contraction Problems
Graph Class or “property”, ᴨ
Forbidden Subgraph Characterization
A graph admits a forbidden subgraph characterization
if, and only if,
it is closed under taking induced subgraphs (hereditary),
that is, the property is preserved under vertex deletions.
If there are finitely many forbidden graphs,
then the corresponding graph modification problem is FPT.

173. Contraction Problems
Graph Class or “property”, ᴨ
Forbidden Subgraph Characterization
A graph admits a forbidden subgraph characterization
if, and only if,
it is closed under taking induced subgraphs (hereditary),
that is, the property is preserved under vertex deletions.
If there are finitely many forbidden graphs,
then the corresponding graph modification problem is FPT.
Not true any more!

174. Contraction To C4-free graphs
Can G be made C4-free by the contraction of at most k edges?
W[2]-hard by a simple reduction from Hitting Set.

175. Contraction To C4-free graphs
Can G be made C4-free by the contraction of at most k edges?
W[2]-hard by a simple reduction from Hitting Set.

177. Ct-free Contraction isW[2]-hard if t ⩾ 4 and FPT if t⩽ 3.
Pt-free Contraction isW[2]-hard if t ⩾ 5 and FPT if t ⩽ 4.
Lokshtanov, M. &
Saurabh
[2013]

178. Ct-free Contraction isW[2]-hard if t ⩾ 4 and FPT if t⩽ 3.
Pt-free Contraction isW[2]-hard if t ⩾ 5 and FPT if t ⩽ 4.
Lokshtanov, M. &
Saurabh
[2013]
Chordal Contraction isW[2]-hard while Clique contraction is FPT
but is unlikely to admit a polynomial kernel.
Cai and Guo
[2013]

179. Ct-free Contraction isW[2]-hard if t ⩾ 4 and FPT if t⩽ 3.
Pt-free Contraction isW[2]-hard if t ⩾ 5 and FPT if t ⩽ 4.
Lokshtanov, M. &
Saurabh
[2013]
Chordal Contraction isW[2]-hard while Clique contraction is FPT
but is unlikely to admit a polynomial kernel.
Characeterizations are open.
Cai and Guo
[2013]

180. Heggernes, van’t Hof,
Lokshtanov & Paul
[2011]
Ct-free Contraction isW[2]-hard if t ⩾ 4 and FPT if t⩽ 3.
Pt-free Contraction isW[2]-hard if t ⩾ 5 and FPT if t ⩽ 4.
Chordal Contraction isW[2]-hard while Clique contraction is FPT
but is unlikely to admit a polynomial kernel.
Contracting to Bipartite graphs is fixed-parameter tractable with
a double-exponential running time.
Lokshtanov, M. &
Saurabh
[2013]
Characeterizations are open.
Cai and Guo
[2013]

181. Heggernes, van’t Hof,
Lokshtanov & Paul
[2011]
Ct-free Contraction isW[2]-hard if t ⩾ 4 and FPT if t⩽ 3.
Pt-free Contraction isW[2]-hard if t ⩾ 5 and FPT if t ⩽ 4.
Chordal Contraction isW[2]-hard while Clique contraction is FPT
but is unlikely to admit a polynomial kernel.
Characeterizations are open.
Contracting to Bipartite graphs is fixed-parameter tractable with
a double-exponential running time.
Lokshtanov, M. &
Saurabh
[2013]
Polynomial kernels are open.
Cai and Guo
[2013]

182. Heggernes, van’t Hof,
Lokshtanov & Paul
[2011]
Ct-free Contraction isW[2]-hard if t ⩾ 4 and FPT if t⩽ 3.
Pt-free Contraction isW[2]-hard if t ⩾ 5 and FPT if t ⩽ 4.
Chordal Contraction isW[2]-hard while Clique contraction is FPT
but is unlikely to admit a polynomial kernel.
Characeterizations are open.
Contracting to Bipartite graphs is fixed-parameter tractable with
a double-exponential running time.
Lokshtanov, M. &
Saurabh
[2013]
Polynomial kernels are open.
Heggernes, van’t Hof,
Lévêque, Lokshtanov
& Paul
[2011]
Contracting to paths is FPT and has a linear-vertex kernel; while
contracting to trees is FPT but is unlikely to admit a polynomial kernel.
Cai and Guo
[2013]

183. Graph Modification
Problems
Completion

184. Chordal Completion

185. Yannakakis
[1981]
Chordal Completion
The minimum fill-in problem is NP-complete
(was left open in the first edition of Garey and Johnson).

186. Yannakakis
[1981]
Chordal Completion
The minimum fill-in problem is NP-complete
(was left open in the first edition of Garey and Johnson).
Kaplan, Shamir &
Tarjan
[1999]
Chordal Completion is fixed-parameter tractable (FPT) with
a running time of O(k616k + k2mn).

187. Yannakakis
[1981]
Chordal Completion
The minimum fill-in problem is NP-complete
(was left open in the first edition of Garey and Johnson).
Kaplan, Shamir &
Tarjan
[1999]
Chordal Completion is fixed-parameter tractable (FPT) with
a running time of O(k616k + k2mn).
Bodlaender,
Heggernes, & Villanger
[2011]
Chordal Completion is fixed-parameter tractable (FPT) with
a running time of O(2.36k + k2mn).

188. Yannakakis
[1981]
Chordal Completion
The minimum fill-in problem is NP-complete
(was left open in the first edition of Garey and Johnson).
Kaplan, Shamir &
Tarjan
[1999]
Chordal Completion is fixed-parameter tractable (FPT) with
a running time of O(k616k + k2mn).
Bodlaender,
Heggernes, & Villanger
[2011]
Chordal Completion is fixed-parameter tractable (FPT) with
a running time of O(2.36k + k2mn).
Fomin & Villanger
[2013]
Chordal Completion admits a sub exponential
parameterized algorithm with a running time of O(2√k log k + k2mn).

189. Interval Completion

190. Kaplan, Shamir &
Tarjan
[1999]
Interval Completion
Chordal Completion, Strongly Chordal Completion, and
Proper Interval Completion are fixed-parameter tractable (FPT).

191. Kaplan, Shamir &
Tarjan
[1999]
Interval Completion
Chordal Completion, Strongly Chordal Completion, and
Proper Interval Completion are fixed-parameter tractable (FPT).
Heggernes, Paul,
Telle & Villanger
[2007]
Interval Completion is fixed-parameter tractable (FPT),
with a running time of O(k2kn3m).

192. Kaplan, Shamir &
Tarjan
[1999]
Interval Completion
Chordal Completion, Strongly Chordal Completion, and
Proper Interval Completion are fixed-parameter tractable (FPT).
Heggernes, Paul,
Telle & Villanger
[2007]
Interval Completion is fixed-parameter tractable (FPT),
with a running time of O(k2kn3m).
Cao
[2007]
Interval Completion has a single-exponential parameterized algorithm,
with a running time of O(6k(n+m)).

193. Kaplan, Shamir &
Tarjan
[1999]
Interval Completion
Chordal Completion, Strongly Chordal Completion, and
Proper Interval Completion are fixed-parameter tractable (FPT).
Heggernes, Paul,
Telle & Villanger
[2007]
Interval Completion is fixed-parameter tractable (FPT),
with a running time of O(k2kn3m).
Cao
[2007]
Interval Completion has a single-exponential parameterized algorithm,
with a running time of O(6k(n+m)).
Bliznets, Fomin,
Pilipczuk & Pilipczuk
[2014]
Interval Completion admits a subexponential parameterized algorithm
with a running time of kO(√k)nO(1).

194. Graph Modification
Problems
A Summary

196. Edge Deletions
Kernels on Planar Graphs & the Meta-Kernel project
Special Graph Classes, eg, Feedback Arc Set on Tournaments
Connectivity Augmentation
The descriptive complexity of graph modification
Structural parameters and other objective functions
Backdoor Sets!