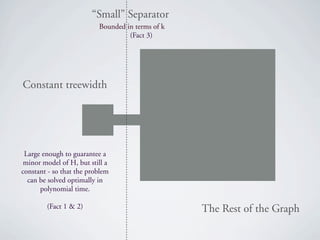
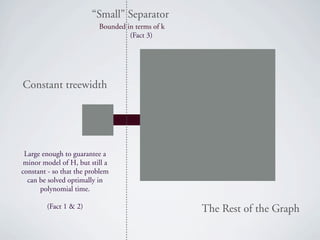
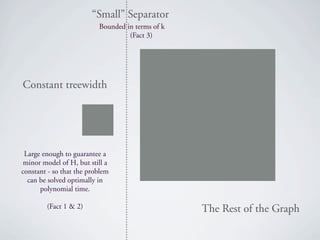
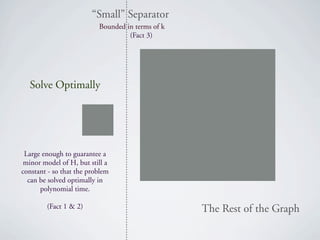
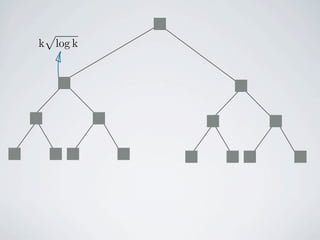
The document discusses kernelization for the F-deletion problem, where graphs in F are connected and at least one is planar. It is shown that the planar F-deletion problem admits a polynomial kernel whenever F contains a planar graph called the "onion" graph. Several other positive and negative results are also presented, including that planar F-deletion admits an approximation algorithm and a polynomial kernel on claw-free graphs. The document concludes by outlining the ingredients for showing that planar F-deletion admits a polynomial kernel.

1. KERNELS
FOR F-DELETION

3. aÉÑáåáíáçåë=
hÉêåÉäë=C=íÜÉ=
cJÇÉäÉíáçå=éêçÄäÉã

4. ^ééêçñáã~íáçå=
dÉííáåÖ=ÅäçëÉ=íç
~å=çéíáã~ä=cJÜáííáåÖ=ëÉí
aÉÑáåáíáçåë=
hÉêåÉäë=C=íÜÉ=
cJÇÉäÉíáçå=éêçÄäÉã

5. ^ééêçñáã~íáçå=
dÉííáåÖ=ÅäçëÉ=íç
~å=çéíáã~ä=cJÜáííáåÖ=ëÉí
aÉÑáåáíáçåë=
hÉêåÉäë=C=íÜÉ=
cJÇÉäÉíáçå=éêçÄäÉã
líÜÉê=RÉëìäíë=
^å=lîÉêîáÉï

6. ^ééêçñáã~íáçå= `çåÅäìÇáåÖ
dÉííáåÖ=ÅäçëÉ=íç RÉã~êâë=
~å=çéíáã~ä=cJÜáííáåÖ=ëÉí
aÉÑáåáíáçåë=
hÉêåÉäë=C=íÜÉ=
cJÇÉäÉíáçå=éêçÄäÉã
líÜÉê=RÉëìäíë=
^å=lîÉêîáÉï

7. ^ééêçñáã~íáçå= `çåÅäìÇáåÖ
dÉííáåÖ=ÅäçëÉ=íç RÉã~êâë=
~å=çéíáã~ä=cJÜáííáåÖ=ëÉí
aÉÑáåáíáçåë=
hÉêåÉäë=C=íÜÉ=
cJÇÉäÉíáçå=éêçÄäÉã
líÜÉê=RÉëìäíë=
^å=lîÉêîáÉï

8. ^ééêçñáã~íáçå= `çåÅäìÇáåÖ
dÉííáåÖ=ÅäçëÉ=íç RÉã~êâë=
~å=çéíáã~ä=cJÜáííáåÖ=ëÉí
aÉÑáåáíáçåë=
hÉêåÉäë=C=íÜÉ=
cJÇÉäÉíáçå=éêçÄäÉã
líÜÉê=RÉëìäíë=
^å=lîÉêîáÉï

9. KERNELIZATION

12. A kernelization procedure
⇤ ⇤
is a function f : {0, 1} N ⇥ {0, 1} N
such that for all (x, k), |x| = n
(f (x, k)) 2 L i (x, k) 2 L
0 0
|x | = g(k) and k k
and f is polynomial time computable.

16. The F-Deletion Problem

17. A classic optimization question
often takes the following general form...

18. A classic optimization question
often takes the following general form...
How “close” is a graph to having a certain property?

19. This question can be formalized in a number of ways,
and a well-studied version is the following:

20. What is the smallest number of vertices that need to be
deleted so that the remaining graph is
__________________?

21. What is the smallest number of vertices that need to be
deleted so that the remaining graph is
independent?

22. What is the smallest number of vertices that need to be
deleted so that the remaining graph is
acyclic?

23. What is the smallest number of vertices that need to be
deleted so that the remaining graph is
planar?

24. What is the smallest number of vertices that need to be
deleted so that the remaining graph is
constant treewidth?

25. What is the smallest number of vertices that need to be
deleted so that the remaining graph is
in X?

26. X = a property

27. A property = an infinite collection of graphs

28. that satisfy the property.
A property = an infinite collection of graphs

29. that satisfy the property.
A property = an infinite collection of graphs
can often be characterized by a finite set of
forbidden minors

30. that satisfy the property.
A property = an infinite collection of graphs
whenever the family is closed under minors,
Graph Minor Theorem
can often be characterized by a finite set of
forbidden minors

31. Independent = no edges
Forbid an edge as a minor

32. Acyclic = no cycles
Forbid a triangle as a minor

33. Planar Graphs
Forbid a K3,3, K5 as a minor

34. Pathwidth-one graphs
Forbid T2, K3 as a minor

35. Remove at most k vertices such that the
remaining graph has no minor models of graphs from F.

36. qÜÉ=cJaÉäÉíáçå=mêçÄäÉã
Remove at most k vertices such that the
remaining graph has no minor models of graphs from F.

37. qÜÉ=cJaÉäÉíáçå=mêçÄäÉã
Remove at most k vertices such that the
remaining graph has no minor models of graphs from F.
NP-Complete
(Lewis, Yannakakis)

38. qÜÉ=cJaÉäÉíáçå=mêçÄäÉã
Remove at most k vertices such that the
remaining graph has no minor models of graphs from F.
NP-Complete FPT
(Lewis, Yannakakis) (Robertson, Seymour)

39. qÜÉ=cJaÉäÉíáçå=mêçÄäÉã
Remove at most k vertices such that the
remaining graph has no minor models of graphs from F.
Polynomial Kernels
NP-Complete FPT
(Lewis, Yannakakis) (Robertson, Seymour)

40. qÜÉ=cJaÉäÉíáçå=mêçÄäÉã
Remove at most k vertices such that the
remaining graph has no minor models of graphs from F.
Polynomial Kernels?
NP-Complete FPT
(Lewis, Yannakakis) (Robertson, Seymour)

41. mä~å~ê
qÜÉ=cJaÉäÉíáçå=mêçÄäÉã
Remove at most k vertices such that the
remaining graph has no minor models of graphs from F.
Polynomial Kernels?
NP-Complete FPT
(Lewis, Yannakakis) (Robertson, Seymour)

42. mä~å~ê
qÜÉ=cJaÉäÉíáçå=mêçÄäÉã
Remove at most k vertices such that the
remaining graph has no minor models of graphs from F.
(Where F contains a planar graph.)
Polynomial Kernels?
NP-Complete FPT
(Lewis, Yannakakis) (Robertson, Seymour)

43. mä~å~ê
qÜÉ=cJaÉäÉíáçå=mêçÄäÉã
Remove at most k vertices such that the
remaining graph has no minor models of graphs from F.
(Where F contains a planar graph.)
Polynomial Kernels?
NP-Complete FPT
(Lewis, Yannakakis) (Robertson, Seymour)
Remark. We assume throughout
that F contains connected graphs.

45. A Summary of Results

46. A Summary of Results
• Planar F-deletion admits an approximation algorithm.

47. A Summary of Results
• Planar F-deletion admits an approximation algorithm.
• Planar F-deletion admits a polynomial kernel on claw-free graphs.

48. A Summary of Results
• Planar F-deletion admits an approximation algorithm.
• Planar F-deletion admits a polynomial kernel on claw-free graphs.
• Planar F-deletion admits a polynomial kernel whenever F contains the
“onion” graph.

49. A Summary of Results
• Planar F-deletion admits an approximation algorithm.
• Planar F-deletion admits a polynomial kernel on claw-free graphs.
• Planar F-deletion admits a polynomial kernel whenever F contains the
“onion” graph.
• The “disjoint” version of the problem admits a kernel.

50. A Summary of Results
• Planar F-deletion admits an approximation algorithm.
• Planar F-deletion admits a polynomial kernel on claw-free graphs.
• Planar F-deletion admits a polynomial kernel whenever F contains the
“onion” graph.
• The “disjoint” version of the problem admits a kernel.
• The onion graph admits an Erdős–Pósa property.

51. A Summary of Results
• Planar F-deletion admits an approximation algorithm.
• Planar F-deletion admits a polynomial kernel on claw-free graphs.
• Planar F-deletion admits a polynomial kernel whenever F contains the
“onion” graph.
• The “disjoint” version of the problem admits a kernel.
• The onion graph admits an Erdős–Pósa property.
• Some packing variants of the problem are not likely to have
polynomial kernels.

52. A Summary of Results
• Planar F-deletion admits an approximation algorithm.
• Planar F-deletion admits a polynomial kernel on claw-free graphs.
• Planar F-deletion admits a polynomial kernel whenever F contains the
“onion” graph.
• The “disjoint” version of the problem admits a kernel.
• The onion graph admits an Erdős–Pósa property.
• Some packing variants of the problem are not likely to have
polynomial kernels.
• The kernelization complexity of Independent FVS and Colorful Motifs
is explored in detail.

53. ^ééêçñáã~íáçå= `çåÅäìÇáåÖ
dÉííáåÖ=ÅäçëÉ=íç RÉã~êâë=
~å=çéíáã~ä=cJÜáííáåÖ=ëÉí
aÉÑáåáíáçåë=
hÉêåÉäë=C=íÜÉ=
cJÇÉäÉíáçå=éêçÄäÉã
líÜÉê=RÉëìäíë=
^å=lîÉêîáÉï

54. ^ééêçñáã~íáçå= `çåÅäìÇáåÖ
dÉííáåÖ=ÅäçëÉ=íç RÉã~êâë=
~å=çéíáã~ä=cJÜáííáåÖ=ëÉí
aÉÑáåáíáçåë=
hÉêåÉäë=C=íÜÉ=
cJÇÉäÉíáçå=éêçÄäÉã
líÜÉê=RÉëìäíë=
^å=lîÉêîáÉï

55. qÜÉ=mä~å~ê=cJaÉäÉíáçå=mêçÄäÉã
Remove at most k vertices such that the
remaining graph has no minor models of graphs from F.
The graphs in F are connected, and at least one of them is planar.

56. Ingredients

57. 1. Let H be a planar graph on h vertices.
If the treewidth of G exceeds ch
then G contains a minor model of H.
2. The planar F-deletion problem can be solved
optimally in polynomial time
on graphs of constant treewidth.
3. Any YES instance of planar F-deletion
has treewidth at most k + ch .

59. Constant treewidth
Large enough to guarantee a
minor model of H, but still a
constant - so that the problem
can be solved optimally in
polynomial time.
(Fact 1 & 2)

60. Constant treewidth
Large enough to guarantee a
minor model of H, but still a
constant - so that the problem
can be solved optimally in
polynomial time.
(Fact 1 & 2) The Rest of the Graph

61. “Small” Separator
Bounded in terms of k
(Fact 3)
Constant treewidth
Large enough to guarantee a
minor model of H, but still a
constant - so that the problem
can be solved optimally in
polynomial time.
(Fact 1 & 2) The Rest of the Graph

62. “Small” Separator
Bounded in terms of k
(Fact 3)
Constant treewidth
Large enough to guarantee a
minor model of H, but still a
constant - so that the problem
can be solved optimally in
polynomial time.
(Fact 1 & 2) The Rest of the Graph

63. “Small” Separator
Bounded in terms of k
(Fact 3)
Constant treewidth
Large enough to guarantee a
minor model of H, but still a
constant - so that the problem
can be solved optimally in
polynomial time.
(Fact 1 & 2) The Rest of the Graph

64. “Small” Separator
Bounded in terms of k
(Fact 3)
Solve Optimally
Large enough to guarantee a
minor model of H, but still a
constant - so that the problem
can be solved optimally in
polynomial time.
(Fact 1 & 2) The Rest of the Graph

65. “Small” Separator
Bounded in terms of k
(Fact 3)
Solve Optimally
Large enough to guarantee a
minor model of H, but still a
constant - so that the problem
can be solved optimally in
polynomial time.
(Fact 1 & 2) Recurse

66. ~å~äóëáë

67. ~å~äóëáë

68. ~å~äóëáë

69. ~å~äóëáë

70. ~å~äóëáë

71. ~å~äóëáë

72. ~å~äóëáë

73. at most k
~å~äóëáë

74. ~å~äóëáë
at most k
at most k
at most k
at most k
at most k
at most k
at most k

75. ~å~äóëáë
at most k
at most k
at most k
at most k
poly(n)
at most k
poly(n)
at most k
poly(n)
at most k
poly(n)
poly(n)

77. How do we get here?

78. 1. Let H be a planar graph on h vertices.
If the treewidth of G exceeds ch
then G contains a minor model of H.
2. The planar F-deletion problem can be solved
optimally in polynomial time
on graphs of constant treewidth.
3. Any YES instance of planar F-deletion
has treewidth at most k + ch .

79. 1. Let H be a planar graph on h vertices.
If the treewidth of G exceeds ch
then G contains a minor model of H.
2. The planar F-deletion problem can be solved
optimally in polynomial time
on graphs of constant treewidth.
3. Any YES instance of planar F-deletion
has treewidth at most k + ch .

81. p
k log k

82. p
k log k

84. Repeat.

85. p
The solution size is proportional to k 2 log k

86. p
The solution size is proportional to k 2 log k
Can be improved to k(log k)3/2 with the help of bootstrapping.

87. Running the algorithm through
values of k between 1 and n (starting from 1)
leads to an approximation
for the optimization version of the problem.

88. ^ééêçñáã~íáçå= `çåÅäìÇáåÖ
dÉííáåÖ=ÅäçëÉ=íç RÉã~êâë=
~å=çéíáã~ä=cJÜáííáåÖ=ëÉí
aÉÑáåáíáçåë=
hÉêåÉäë=C=íÜÉ=
cJÇÉäÉíáçå=éêçÄäÉã
líÜÉê=RÉëìäíë=
^å=lîÉêîáÉï

89. ^ééêçñáã~íáçå= `çåÅäìÇáåÖ
dÉííáåÖ=ÅäçëÉ=íç RÉã~êâë=
~å=çéíáã~ä=cJÜáííáåÖ=ëÉí
aÉÑáåáíáçåë=
hÉêåÉäë=C=íÜÉ=
cJÇÉäÉíáçå=éêçÄäÉã
líÜÉê=RÉëìäíë=
^å=lîÉêîáÉï

90. qÜÉ=cJaÉäÉíáçå=mêçÄäÉã
Remove at most k vertices such that the
remaining graph has no minor models of graphs from F.
Polynomial Kernels?
NP-Complete FPT
(Lewis, Yannakakis) (Robertson, Seymour)

91. Conjecture

92. qÜÉ=cJaÉäÉíáçå=mêçÄäÉã
Remove at most k vertices such that the
remaining graph has no minor models of graphs from F.

93. qÜÉ=cJaÉäÉíáçå=mêçÄäÉã
Remove at most k vertices such that the
remaining graph has no minor models of graphs from F.
The problem admits polynomial kernels when F contains a planar graph.

94. qÜÉ=cJaÉäÉíáçå=mêçÄäÉã
Remove at most k vertices such that the
remaining graph has no minor models of graphs from F.
On Claw free graphs
The problem admits polynomial kernels when F contains a planar graph.

95. qÜÉ=cJaÉäÉíáçå=mêçÄäÉã
Remove at most k vertices such that the
remaining graph has no minor models of graphs from F.
particular
The problem admits polynomial kernels when F contains a planar graph.

97. Protrusion-based reductions
the idea

98. A Boundary of Constant Size
Constant Treewidth

99. A Boundary of Constant Size
Constant Treewidth

100. A Boundary of Constant Size
Constant Treewidth

104. The space of t-boundaried graphs
can be broken up into equivalence classes
based on how they “behave” with
the “other side” of the boundary.

107. The value of the
optimal solution
is the same
up to a constant.

108. The space of t-boundaried graphs
can be broken up into equivalence classes
based on how they “behave” with
the “other side” of the boundary.

109. The space of t-boundaried graphs
can be broken up into equivalence classes
based on how they “behave” with
the “other side” of the boundary.
For some problems,
the number of equivalence classes is finite,
allowing us to replace protrusions in graphs.

110. For the protrusion-based reductions to take effect,
we require subgraphs of constant treewidth
that are separated from the rest of the graph by
a constant-sized separator.

111. Approximation Algorithm
For the protrusion-based reductions to take effect,
we require subgraphs of constant treewidth
that are separated from the rest of the graph by
a constant-sized separator.

112. F-hitting Set
Constant Treewidth

113. Approximation Algorithm
For the protrusion-based reductions to take effect,
we require subgraphs of constant treewidth
that are separated from the rest of the graph by
a constant-sized separator.

114. Approximation Algorithm
For the protrusion-based reductions to take effect,
we require subgraphs of constant treewidth
that are separated from the rest of the graph by
a constant-sized separator.
Restrictions like claw-freeness.

115. ^ééêçñáã~íáçå= `çåÅäìÇáåÖ
dÉííáåÖ=ÅäçëÉ=íç RÉã~êâë=
~å=çéíáã~ä=cJÜáííáåÖ=ëÉí
aÉÑáåáíáçåë=
hÉêåÉäë=C=íÜÉ=
cJÇÉäÉíáçå=éêçÄäÉã
líÜÉê=RÉëìäíë=
^å=lîÉêîáÉï

116. ^ééêçñáã~íáçå= `çåÅäìÇáåÖ
dÉííáåÖ=ÅäçëÉ=íç RÉã~êâë=
~å=çéíáã~ä=cJÜáííáåÖ=ëÉí
aÉÑáåáíáçåë=
hÉêåÉäë=C=íÜÉ=
cJÇÉäÉíáçå=éêçÄäÉã
líÜÉê=RÉëìäíë=
^å=lîÉêîáÉï

117. crRqebR=afRb`qflkp

118. crRqebR=afRb`qflkp
• What happens when we drop the planarity assumption?

119. crRqebR=afRb`qflkp
• What happens when we drop the planarity assumption?
• What happens if there are graphs in the forbidden set that are
not connected?

120. crRqebR=afRb`qflkp
• What happens when we drop the planarity assumption?
• What happens if there are graphs in the forbidden set that are
not connected?
• Are there other infinite classes of graphs (not captured by finite
sets of forbidden minors) for which the same reasoning holds?

121. crRqebR=afRb`qflkp
• What happens when we drop the planarity assumption?
• What happens if there are graphs in the forbidden set that are
not connected?
• Are there other infinite classes of graphs (not captured by finite
sets of forbidden minors) for which the same reasoning holds?
• How do structural requirements on the solution
(independence, connectivity) affect the complexity of the
problem?

122. ^`hkltibadjbkqp

123. ^`hkltibadjbkqp
Abhimanyu M. Ambalath, S. Arumugam,
Radheshyam Balasundaram, K. Raja Chandrasekar,
Michael R. Fellows, Fedor V. Fomin,
Venkata Koppula, Daniel Lokshtanov, Matthias Mnich
N. S. Narayanaswamy, Geevarghese Philip,
Venkatesh Raman, M. S. Ramanujan, Chintan Rao H.,
Frances A. Rosamond, Saket Saurabh,
Somnath Sikdar, Bal Sri Shankar

124. Thank you!