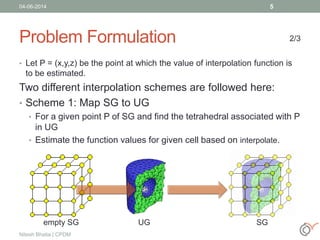
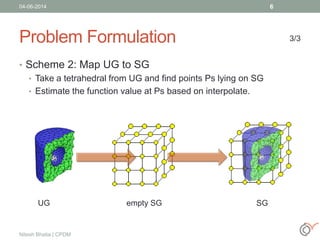
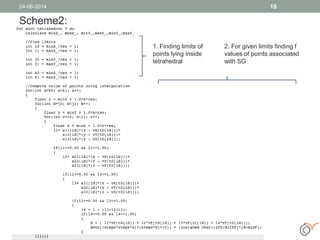
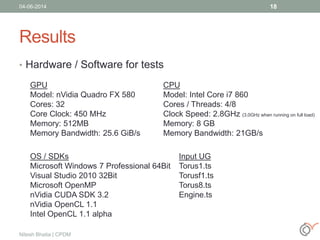
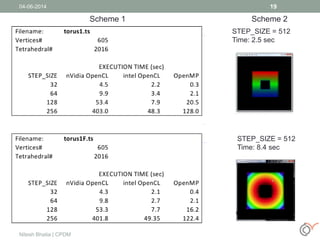
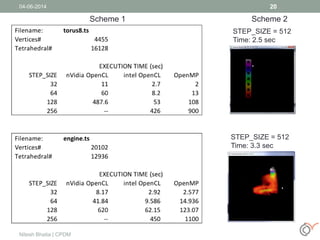
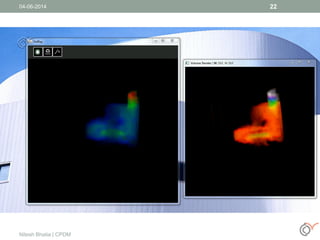
This document discusses the process of volume rendering for unstructured tetrahedral grids, detailing interpolation techniques and implementation methods. It outlines two mapping schemes from unstructured to structured grids and presents a three-step approach to computation and visualization using OpenCL or OpenMP. Results from tests are also provided, demonstrating the performance of different schemes implemented on hardware and software setups.

1. VOLUME RENDERING OF
UNSTRUCTURED TETRAHEDRAL GRIDS

2. Flow
• Introduction
• Problem Formulation
• Tetrahedral Interpolation
• Implementation
• Results
• Demo
• Endnotes
04-06-2014
Nitesh Bhatia | CPDM
2

3. Introduction: Volume Rendering
• Volume rendering is a technique that can
be used to visualize sampled 3D scalar
data as a continuous medium or extract
features.
Most algorithms for direct volume rendering
have assumed structured data in form of
rectilinear grid.
• In this project we worked on a method for
rendering unstructured volume; volume
represented by group of tetrahedrals.
04-06-2014
Nitesh Bhatia | CPDM
3

4. Problem Formulation
• The idea is to convert unstructured input tetrahedral grid
(UG) to output structured regular grid (SG) and render it
using existing ray casting system.
• The data represented in UG must be interpolated to
produce SG.
• The UG consists of tetrahedrals bounded by four vertices
numbered 1,2,3,4, the coordinates of ith vertex being (xi,
yi, zi) and associated data value is denoted fi.
• The data values are assumed to be the values of an
unknown locally smooth trivariate function
interpolate discussed in next heading.
04-06-2014
Nitesh Bhatia | CPDM
4
1/3

5. Problem Formulation
• Let P = (x,y,z) be the point at which the value of interpolation function is
to be estimated.
Two different interpolation schemes are followed here:
• Scheme 1: Map SG to UG
• For a given point P of SG and find the tetrahedral associated with P
in UG
• Estimate the function values for given cell based on interpolate.
04-06-2014
Nitesh Bhatia | CPDM
5
empty SG UG SG
2/3

6. Problem Formulation
• Scheme 2: Map UG to SG
• Take a tetrahedral from UG and find points Ps lying on SG
• Estimate the function value at Ps based on interpolate.
04-06-2014
Nitesh Bhatia | CPDM
6
UG empty SG SG
3/3

7. Tetrahedral Interpolation: interpolate
• Given a tetrahedron T with vertices v1, v2, v3, v4 and
function value associated with these vertices be f1, f2, f3
and f4, the problem is to find interpolated function value f
for any given point P.
04-06-2014
Nitesh Bhatia | CPDM
7
.P(f)
v1(f1)
v2(f2)v4(f4)
v3(f3)
1/4

8. Tetrahedral Interpolation: interpolate
Geometric Solution
• Take ratio of perpendicular distance of P
to a face with perpendicular distance of
opposite vertex to that face.
• Find these ratios with all four faces and
name them l1, l2, l3 and l4.
• If the point P is lying inside tetrahedral
these ratios will come between 0 and 1.
• Sum of these ratios will always be 1.
• These l1,l2, l3 and l4 are known as
barycentric coordinates of point P with
respect to tetrahedral T.
• f = l1*f1 + l2*f2 + l3*f3 + l4*f4
04-06-2014 8
2/4
Nitesh Bhatia | CPDM

9. Tetrahedral Interpolation: interpolate
• Mathemetical Interpretation
04-06-2014
Nitesh Bhatia | CPDM
9
3/4

10. Tetrahedral Interpolation: interpolate
04-06-2014
Nitesh Bhatia | CPDM
10
4/4

11. Implementation
In implementation we are following 3 step approach
1. Load the vertices and tetrahedron information from
given .ts file into CPU memory
2. Based on two schemes presented, perform
computations using OpenCL (or OpenMP) to form a
regular grid
3. Display the grid by Ray Casting in OpenCL using CL-GL
Interoperability.
04-06-2014
Nitesh Bhatia | CPDM
11

12. Implementation: Description
Step1:
• The data set given .ts file is form of list of vertices with 3D
coordinates and associated function value and then a list of
tetrahedrons with asociated 4 vertices.
• We are first loading this information into memory.
• While loading the vertices we are computing minimum and
maximum values for (x,y,z) coordinates and storing it as minX,
minY, minZ, maxX, maxY, maxZ.
• We are then finding the difference between these minimum and
maximum values and storing it as diffX, diffY, diffZ.
• We are then computing diff equal to maximum of diffX, diffY
and diffZ.
• We are then finding dimensions of our bounding box with side
equal to diff.
04-06-2014
Nitesh Bhatia | CPDM
12

13. Step 2:
• Given
• We are computing A-1 for each tetrahedron
• We define a constant STEP_SIZE = 128 (or any other
value) which gives dimension of our volume as
128*128*128.
• We are setting the resolution (step size) of our volume as
res = diff / STEP_SIZE
04-06-2014
Nitesh Bhatia | CPDM
13

14. Scheme 1:
04-06-2014
Nitesh Bhatia | CPDM
14
1. Finding point lying
on SG
2. searching for
associated T in UG
and finding f value
using interpolation

15. • This scheme is implemented in both OpenCL and
OpenMP
• In OpenMP implementation we are adding following two
lines as compiler directive in starting of loop:
• #paragma omp set_num_threads(8)
• #paragma omp parallel for shared(i,j,k)
• In OpenCL implementation we are setting our dimensions
as 1D with
• size_t global_size = {STEP_SIZE * STEP_SIZE * STEP_SIZE}
• Here we are Parallelizing in terms of volume element
04-06-2014
Nitesh Bhatia | CPDM
15

16. Scheme2:
04-06-2014
Nitesh Bhatia | CPDM
16
1. Finding limits of
points lying inside
tetrahedral
2. For given limits finding f
values of points associated
with SG

17. • Scheme 2 is implemented in OpenCL. We are setting our
dimensions as 1D with
size_t global_size = tet_qty
• Here we are Parallelizing in terms of tetrahedral quantity
Step 3:
• We are then giving this 1D grid of function values to
existing ray tracer (provided by nVidia in their SDK) as
input.
04-06-2014
Nitesh Bhatia | CPDM
17

18. Results
• Hardware / Software for tests
04-06-2014
Nitesh Bhatia | CPDM
18
GPU
Model: nVidia Quadro FX 580
Cores: 32
Core Clock: 450 MHz
Memory: 512MB
Memory Bandwidth: 25.6 GiB/s
CPU
Model: Intel Core i7 860
Cores / Threads: 4/8
Clock Speed: 2.8GHz (3.0GHz when running on full load)
Memory: 8 GB
Memory Bandwidth: 21GB/s
OS / SDKs
Microsoft Windows 7 Professional 64Bit
Visual Studio 2010 32Bit
Microsoft OpenMP
nVidia CUDA SDK 3.2
nVidia OpenCL 1.1
Intel OpenCL 1.1 alpha
Input UG
Torus1.ts
Torusf1.ts
Torus8.ts
Engine.ts

19. 04-06-2014
Nitesh Bhatia | CPDM
19
Scheme 1 Scheme 2
STEP_SIZE = 512
Time: 8.4 sec
STEP_SIZE = 512
Time: 2.5 sec

20. 04-06-2014
Nitesh Bhatia | CPDM
20
Scheme 1 Scheme 2
STEP_SIZE = 512
Time: 2.5 sec
STEP_SIZE = 512
Time: 3.3 sec

21. 04-06-2014
Nitesh Bhatia | CPDM
21

22. 04-06-2014
Nitesh Bhatia | CPDM
22

23. • Demo Video URL:
https://www.youtube.com/watch?v=CaBuZ7
se7-o
04-06-2014
Nitesh Bhatia | CPDM
23

24. Impressions
• Learning OpenCL was a challenging task but we it was
interesting.
• Debugging OpenCL is difficult task as stream output
(“printf” function) cannot be called in openCL kernel. In
Intel’s compiler is based on OpenCL 1.1 in which “printf” is
supported.
• Double precision computations are not supported on my
card.
• Graphic Driver Crash Problem
04-06-2014
Nitesh Bhatia | CPDM
24

25. “We now know a thousand ways not to
build a light bulb”
04-06-2014
Nitesh Bhatia | CPDM
25
THANKS !