ObliVM

ObliVM
A. Satapathy1 C. Soni2
1,2Information and Communication Laboratory
Industrial Technology Research Institute
Taiwan
Under the guidance of Dr. Tzi-cker Chiueh
2017, July 28th
A. Satapathy, C. Soni ObliVM 2017, July 28th
1 / 82

Outline
1 Acknowledgement
2 Introduction
Overview
Programmer’s View
Features
3 Programming Language
Standard Types
Generic Types
Native Types
Program Execution Trace
Loop Coalescing
4 Applications
MapReduce
Circuit ORAM
Karatsuba Multiplication
Stack
Dijkstra Algorithm
5 ObliVM Compiler
Environment Preparation
Compilation Process
Execution Process
Input Preparation
6 Results
Input Preparation
Compilation
Execution
7 Summary
8 References
2 / 82

Acknowledgement
”ObliVM has developed by Chang Liu, Xiao Shaun Wang,
Kartik Nayak, Yan Huang and Elaine Shi
from University of Maryland and Indiana University.”
3 / 82

Outline
1 Acknowledgement
2 Introduction
Overview
Programmer’s View
Features
Standard Types
Generic Types
Native Types
Loop Coalescing
4 Applications
MapReduce
Circuit ORAM
Stack
Dijkstra Algorithm
5 ObliVM Compiler
Compilation Process
Execution Process
Input Preparation
6 Results
Input Preparation
Compilation
Execution
7 Summary
8 References
4 / 82

Overview
A programming framework for secure multi party computation which
supports user friendly programming abstraction.
Presently, it uses Improved 2-party Garbled circuit protocol at
backend.
ObliVM compiler compiles program to circuit representations whose
inputs are oblivious memory accesses.
It oﬀers a reusable framework to implement and distribute new
cryptographic algorithms.
It can be used to develop various applications in the ﬁeld of data
mining, streaming algorithms, graph algorithms, data structures etc.
5 / 82

Outline
1 Acknowledgement
2 Introduction
Overview
Programmer’s View
Features
Standard Types
Generic Types
Native Types
Loop Coalescing
4 Applications
MapReduce
Circuit ORAM
Stack
Dijkstra Algorithm
5 ObliVM Compiler
Compilation Process
Execution Process
Input Preparation
6 Results
Input Preparation
Compilation
Execution
7 Summary
8 References
6 / 82

Programmer’s View
As an Expert Programmer
Easily extend the system with rich, optimized libraries or customized
cryptographic protocols.
Develop and export those libraries as a standard/native/generic types
and functions, in the source language.
As a Non-specialist Programmer
Write programs using above standard/native/generic data types and
functions.
ObliVM compiler compiles the program to an eﬃcient secure
computation protocol.
7 / 82

Outline
1 Acknowledgement
2 Introduction
Overview
Programmer’s View
Features
Standard Types
Generic Types
Native Types
Loop Coalescing
4 Applications
MapReduce
Circuit ORAM
Stack
Dijkstra Algorithm
5 ObliVM Compiler
Compilation Process
Execution Process
Input Preparation
6 Results
Input Preparation
Compilation
Execution
7 Summary
8 References
8 / 82

Features
ObliVM language builds on top of the SCVM language which oﬀers
scalability to big data.
Apart from standard features it supports generic and native type
primitives.
It has addressed the key requirement, program execution traces will
not leak information.
These execution traces include memory instruction trace, function
stack trace and declassiﬁcation trace.
9 / 82

Outline
1 Acknowledgement
2 Introduction
Overview
Programmer’s View
Features
Standard Types
Generic Types
Native Types
Loop Coalescing
4 Applications
MapReduce
Circuit ORAM
Stack
Dijkstra Algorithm
5 ObliVM Compiler
Compilation Process
Execution Process
Input Preparation
6 Results
Input Preparation
Compilation
Execution
7 Summary
8 References
10 / 82

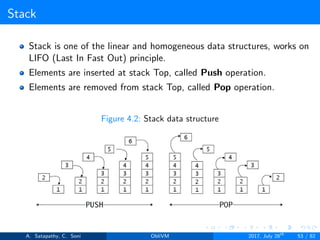
Standard Types
Variables or arrays are either of a secure or public type.
secure variables or arrays are secretly shared between two parties.
i.e. neither party sees the value.
public variables or arrays are seen by both parties.
secure int10[public 1000] keys: Array contents are secret shared
but indices to array are public. No ORAM is used. 10 in int10
indicated 10 bits key value.
secure int10[secure 1000] keys: Array contents are secret shared
and indices to array are secure. Trivial ORAM is used. 10 in int10
indicated 10 bits key value.
public int10[public 1000] keys : Arrays contents are seen by
both parties.
11 / 82

Standard Types
Figure 3.1: Data distribution of secure int10[public 4] P1 and
secure int10[public 4] P2 and their access
12 / 82

Standard Types
Figure 3.2: Data distribution of secure int10[secure 4] P1 and
secure int10[secure 4] P2 and their access
13 / 82

Outline
1 Acknowledgement
2 Introduction
Overview
Programmer’s View
Features
Standard Types
Generic Types
Native Types
Loop Coalescing
4 Applications
MapReduce
Circuit ORAM
Stack
Dijkstra Algorithm
5 ObliVM Compiler
Compilation Process
Execution Process
Input Preparation
6 Results
Input Preparation
Compilation
Execution
7 Summary
8 References
14 / 82

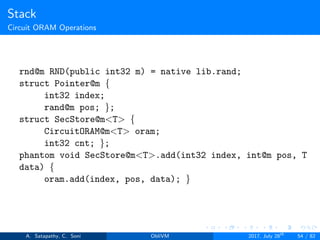
Generic Types
Generic Variable
ObliVM uses ’struct’ keyword to deﬁne composite data type.
It supports generic data type like C++ template.
Suppose a binary tree with public key value but secret node data can
be deﬁned using struct. node size is 1000.
struct KeyValueTable<T>{
secure int10[public 1000] keys;
T[public 1000] values;
};
Generic type T similar to template in C++. Data type T to be
secret-shared.
15 / 82

Generic Types
Generic Constant
ObliVM supports generic constants to improve ﬂexibility and
reusability of programming language. An example is given below.
struct TreeNode@m<T>{
public int@m key;
T value;
public int@m left, right;
};
struct Tree@m<T>{
TreeNode<T>[public (1<<m) - 1] nodes;
public int@m root;
};
@m is the generic constant. Here @m indicates m bits integer.
16 / 82

Generic Types
Generic Function
ObliVM supports generic functions to bring modularity in program.
A generic function, to search the value associated with a given key in
previously deﬁned binary tree is given below.
T Tree@m<T>.search(public int@m key){
public int@m now = this.root, tk;
T ret;
while (now != -1){
tk = this.nodes[now].key;
if (tk == key) {ret = this.nodes[now].value;}
if(tk <= key) {now = this.nodes[now].right;}
else {now = this.nodes[now].left}; }
return ret; }
17 / 82

Outline
1 Acknowledgement
2 Introduction
Overview
Programmer’s View
Features
Standard Types
Generic Types
Native Types
Loop Coalescing
4 Applications
MapReduce
Circuit ORAM
Stack
Dijkstra Algorithm
5 ObliVM Compiler
Compilation Process
Execution Process
Input Preparation
6 Results
Input Preparation
Compilation
Execution
7 Summary
8 References
18 / 82

Native Types
Native Data Types
ObliVM supports native data types for homomorphic encryption.
ObliVM-GC is implemented in JAVA. To handle large integer, JAVA
class ”Biginteger” is used.
typedef BigInt@m = native BigInteger;
BigInt@m x;
19 / 82

Native Types
Native Functions
ObliVM supports four native functions. They are add, multiply,
fromInt and toInt.
First two operations are arithmetic operations and last two are used
for conversion between GC based integer and HE based integer.
BigInt@m BigInt@m.add(BigInt@m x, BigInt@m y) =
native BigInteger.add;
BigInt@m BigInt@m.multiply(BigInt@m x, BigInt@m y) =
native BigInteger.multiply;
BigInt@m BigInt@m.fromInt(int@m y) =
native BigInteger.fromInt;
int@m BigInt@m.toInt(BigInt@m x) =
native BigInteger.toInt;
20 / 82

Outline
1 Acknowledgement
2 Introduction
Overview
Programmer’s View
Features
Standard Types
Generic Types
Native Types
Loop Coalescing
4 Applications
MapReduce
Circuit ORAM
Stack
Dijkstra Algorithm
5 ObliVM Compiler
Compilation Process
Execution Process
Input Preparation
6 Results
Input Preparation
Compilation
Execution
7 Summary
8 References
21 / 82

ObliVM provides security against leakage of information from
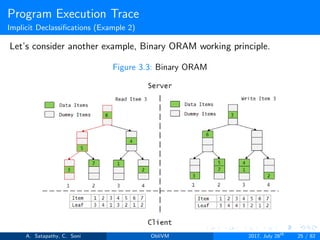
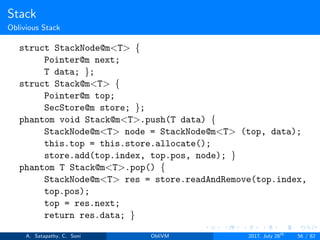
program execution traces.
These execution traces are memory and instruction trace, stack
/function trace and rand. no. declassiﬁcation trace.
To prevent information leakage, Trivial ORAM or any oblivious data
structure is used to implement oblivious memory and instruction trace.
Oblivious data structure can be Square Root ORAM, Hierarchical
ORAM, Binary ORAM, Path ORAM or Circuit ORAM.
Oblivious stack trace is implemented by the help of phantom function.
At last, rand. no. must be implicitly declassiﬁed at most one time i.e.
once the value is public, rand. no. value must be changed.
22 / 82

Rand. No. Trace
rnd@m RND(public int32 m)
Function RND returns random m bits. Here m is a 32 bits integer.
In ObliVM, Rand. no. always secretly shared between the parties.
Rand. no. is declassified by assigning it to a public variable.
Declassification is called implicity declassification, if rand. value is
public without any precomputation.
So, rand. no. must be implicity declassified at most once. Once the
value is public, rand. no. value must be changed.
23 / 82

Implicit Declassifications (Example 1)
Let us consider an example for rand. no. implicit declassification.
rnd32 r = RND(32), x;
if (s) x = r;
else x = RND(32);
........
public int32 p = x;
public int32 q = r;
if s = 1 then public variables ’p’ and ’q’ contain ’r’ value. Here ’r’
value is disclosed twice.
To prevent this, rand. variable value must be updated after first
revelation.
24 / 82

Implicit Declassiﬁcations (Example 2)
Let’s consider another example, Binary ORAM working principle.
Figure 3.3: Binary ORAM
25 / 82

Implicit Declassiﬁcations (Example 2 Cont.)
In binary ORAM, element will be de-allocated once it found and
written back to root.
Scanning happened in the element’s assigned path which is a random
value.
Path number (i.e. random value) of current element is revealed to
server before scanning.
So, in binary ORAM, path number is changed after scanning to
prevent information leakage.
26 / 82

Stack/Function Trace
Let’s consider a native function implementation.
secure int32 prefixSum (public int32 n){
secure int32 ret = a[n];
a[n] = 0;
if (n != 0) ret + prefixSum (n - 1);
return ret;
}
If n != 0 is true, prefixSum will be executed which made function
trace unoblivious. To avoid this, phantom keyword is used.
27 / 82

Oblivious Stack/Function Trace
Function call within a secret conditional statement will be made
oblivious with the help of phantom keyword.
phatom function is executed in dual modes. One is ’real’ and other
one is ’phantom’.
In ’real’ mode, all the statements inside the function are executed and
real changes are taken place.
In ’phantom’ mode, it simulates memory and instruction trace
without any changes. Let’s consider an example in next slide.
28 / 82

Phantom Function
phantom secure int32 prefixSum (public int32 n){
secure int32 ret = a[n];
a[n] = 0;
if (n != 0) ret + prefixSum (n - 1);
return ret;
}
Here prefixSum is a phantom function. function prefixSum will be
called, even if ’n != 0’ is false.
If condition is true, ’0’ will be assigned to ’a’. If condition is false,
value of ’a’ will not change i.e the previous value is retained.
Both cases, same amount of memory traces are generated.
29 / 82

Phantom Function (Cont...)
prefixSum(idx, indicator)
The compiler will generate code which contains the above signature
If indicator is false, function will run in real mode. If true, function
will run in phantom mode.
It’s diﬃcult for an adversary to diﬀerentiate between real execution
and phantom execution.
30 / 82

Outline
1 Acknowledgement
2 Introduction
Overview
Programmer’s View
Features
Standard Types
Generic Types
Native Types
Loop Coalescing
4 Applications
MapReduce
Circuit ORAM
Stack
Dijkstra Algorithm
5 ObliVM Compiler
Compilation Process
Execution Process
Input Preparation
6 Results
Input Preparation
Compilation
Execution
7 Summary
8 References
31 / 82

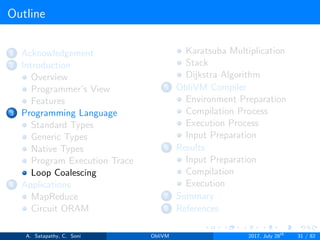
Loop Coalescing
The process of converting nested loops to a single loop is called loop
coalescing. It is used for code optimization.
It gains performance on certain architecture. It reduces higher
dimensional loop to a single dimension.
for (i = 0; i < N; i++) {
for (j = 0; j < M;
j++) {
a[i][j]=b[i][j];
}
}
for (ij = 0; i < MN; ij++)
{
i = ij / M;
j = ij % M;
a[i][j]=b[i][j];
}
32 / 82

Outline
1 Acknowledgement
2 Introduction
Overview
Programmer’s View
Features
Standard Types
Generic Types
Native Types
Loop Coalescing
4 Applications
MapReduce
Circuit ORAM
Stack
Dijkstra Algorithm
5 ObliVM Compiler
Compilation Process
Execution Process
Input Preparation
6 Results
Input Preparation
Compilation
Execution
7 Summary
8 References
33 / 82

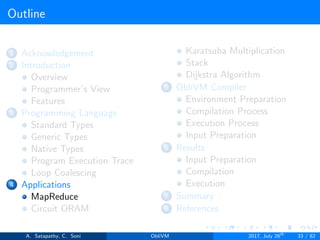
MapReduce
MapReduce algorithm has two functions. MAP and REDUCE.
MAP under MAPPER class, takes input and tokenizes it.
REDUCE under REDUCER class, ﬁnds matching pairs and reduce
them.
Algorithm (Map)
Given: int K[ ] = {ki}i ∈ [n]. ki ∈ domain ’D’
1: function MAP(int K[ ])
2: Initialize C ← Φ
3: for i = 1 to n do:
4: C ← C (ki, 1)
5: end for
6: return C
7: end function
34 / 82

MapReduce
Algorithm (Reduce)
Given: (k1, v1), (k2, v2), (k3, v3), ....,(kj, vj).
1: Initialize int Z[ ] ← 0, t ← 0.
2: for i = 1 to j do:
3: if ki = k do:
4: Z[t] ← vi.
5: t ← t + 1
6: function REDUCE(int k, int Z[ ])
7: Initialize Sum ← 0, n ← |Z[ ]|
8: for i = 1 to n do:
9: Sum ← Sum + Z[i]
10: return Sum
11: end function
35 / 82

MapReduce
Example: Evaluate frequency of each character in a text ﬁle using
MapReduce algorithms.
Figure 4.1: Character frequency calculation in MapReduce.
36 / 82

MapReduce
Oblivious MapReduce
A sequential implementation of MapReduce algorithm which runs on a
processor thread.
By default MAP function is oblivious. It is done by sequential scan
over the data.
In REDUCE operation, oblivious sort algorithm is used to group the
pairs having same key values.
For last (ki, vi) pair of each group, replace vi with sum. Replace other
vi in groups with ⊥.
Apply oblivious sort to relocate ⊥ to the end.
37 / 82

MapReduce
Oblivious MapReduce
Let’s take the example in slide no. 36 and solve it using oblivious
MapReduce algorithm.
Table 4.1: Input arrray.
A B R C C R A C B
MAPPER makes sequential scan over input array and assigns ’1’ to each
element.
Table 4.2: Resultant key value pairs after Mapping.
A B R C C R A C B
1 1 1 1 1 1 1 1 1
38 / 82

MapReduce
Oblivious MapReduce
REDUCER, ﬁrst groups the pairs having same key values. Oblivious
sorting algorithm is used to move items having key value.
Table 4.3: Sorted key value pairs.
A A B B C C C R R
1 1 1 1 1 1 1 1 1
REDUCER, for last (ki, vi) of ki, write the sum. Else write dummy ’⊥’
Table 4.4: Key value pairs after reduction.
A A B B C C C R R
⊥ 2 ⊥ 2 ⊥ ⊥ 3 ⊥ 2
39 / 82

MapReduce
Oblivious MapReduce
Apply oblivious sort to move all the dummies to end of the array.
Table 4.5: Sorted key value pairs based on values.
A B R C A B C C R
2 2 2 3 ⊥ ⊥ ⊥ ⊥ ⊥
Table 4.6: Final output after dummies elimination.
A B R C
2 2 2 3
40 / 82

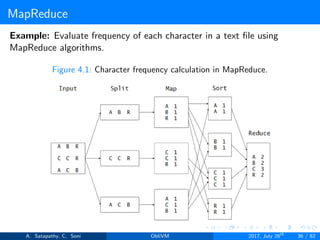
MapReduce
Oblivious MapReduce
Pair<K,V>[public n] MapReduce@m@n<I,K,V>(I[public m]
data, Pair<K,V> map(I), V reduce(K,V,V), V initialVal,
int2 cmp(K, K)) {
public int32 i;
Pair<K,V>[public m] d2;
for (i = 0; i<m; i++)
d2[i] = map(data[i])
sort@m<K,V>(d2, 1, cmp);
K key = d2[0].k;
V val = initialVal;
Pair<int1, Pair<K,V>>[public m] res;
for (i = 0; i<m; i++) {
res[i].v.k = key;
res[i].v.v = val;
if (cmp(key, d2[i+1].k)) == 0 {
41 / 82

MapReduce
Oblivious MapReduce
res[i].k.val = 1; }
else {
res[i].k.val = 0;
key = d2[i+1].k;
val = initialVal; }
val = reduce(key, val, d2[i+1].v); }
res[m-1].k.val = 0;
res[m-1]v.k = key;
res[m-1].v.v = val;
sort@m<int1, Pair<K,V>>(res, 1, zeroOneCmp);
Pair<K,V>[public n] top;
for (i = 0; i < n; i = i+1)
top[i] = res[i].v;
return top; }
42 / 82

MapReduce
Oblivious MapReduce
1: int2 cmp(int32 x, int32 y) {
2: int2 r = 0;
3: if (x<y) r = -1;
4: else if (x > y) r = 1;
5: return r; }
1: Pair<int32, int32>map(int32 x){
2: return Pair<int32, int32>(x,1); }
1: int reduce(int32 k, int32 v1, int32 v2) {
2: return v1 + v2 }
c = MapReduce@m@n<int32, int32, int32>(a, map, reduce,
cmp, 1);
(Oblivious MapReduce calling function)
43 / 82

Outline
1 Acknowledgement
2 Introduction
Overview
Programmer’s View
Features
Standard Types
Generic Types
Native Types
Loop Coalescing
4 Applications
MapReduce
Circuit ORAM
Stack
Dijkstra Algorithm
5 ObliVM Compiler
Compilation Process
Execution Process
Input Preparation
6 Results
Input Preparation
Compilation
Execution
7 Summary
8 References
44 / 82

Circuit ORAM
Circuit ORAM is the optimized ORAM available till today.
Amortized cost will be reduced futher by upgrading binary ORAM to
Circuit ORAM.
Most suitable for MPC as it takes least number of AND and OR
gates for circuit implementaion.
Data items are stored in encrypted form of (indexi || datai).
As the level increases, the number of buckets / nodes at each level
also increases by a factor of two.
While reading a perticular element, scan all the buckets in the path.
When found, delete it from the bucket and store it in the stash.
While writing, rearrange the read element and elements in its newly
assigned path. It minimizes rearrangement cost to O(log2N).
45 / 82

Circuit ORAM
#define BUCSIZE 3
#define STASHSIZE 33
struct Block@n<T> {
int@n id, pos;
T data; };
struct CircuitOram@n<T> {
dummy Block@n<T>[public 1<<n+1][public BUCSIZE]
buckets;
dummy Block@n<T>[public STASHSIZE] stash; };
phantom T CircuitOram@n<T>.readAndRemove (int@n id,
rnd@n pos) {
public int32 pubPos = pos;
public int32 i = (1 << n) + pubPos;
T res;
for (public int32 k = n; k>=0; k=k-1) {
for (public int32 j=0;j<BUCSIZE;j=j+1) {
46 / 82

Circuit ORAM
if (buckets[i][j] != null &&
buckets[i][j].id == id){
res = buckets[i][j].data;
buckets[i][j] = null; } }
i = (i-1) / 2; }
for (public int32 i=0;i<STASHSIZE;i=i+1) {
if (stash[i]!=null && stash[i].id==id) {
res = stash[i].data;
stash[i] = null; } }
return res;}
47 / 82

Outline
1 Acknowledgement
2 Introduction
Overview
Programmer’s View
Features
Standard Types
Generic Types
Native Types
Loop Coalescing
4 Applications
MapReduce
Circuit ORAM
Stack
Dijkstra Algorithm
5 ObliVM Compiler
Compilation Process
Execution Process
Input Preparation
6 Results
Input Preparation
Compilation
Execution
7 Summary
8 References
48 / 82

Karatsuba multiplication solves multiplication of two n bits numbers
using recursion. complexity is O(nlog23)
x = a × 2n/2 + b, y = c × 2n/2 + d. where x and y are inputs.
t1 = a × c, t2 = b × d, t3 = (a+b)×(c+d)
x×y = t1<<n + t2 + (t3 - t1 -t2)<<(n/2)
Same procedures have to be followed for a×c and b×d. Whole
problem is solved in recursive way.
49 / 82

int@(2∗n) karatsubaMult@n(int@x, int@y) {
int@(2∗n) ret;
if (n < 10) {
ret = x∗y; }
else {
int@(n - n/2) a = x$n/2 ∼ n$;
int@(n/2) b = x$0 ∼ n/2$;
int@(n - n/2) c = y$n/2 ∼ n$;
int@(n/2) d = y$0 ∼ n/2$;
int@(2 ∗ (n - n/2)) t1 = karatsubaMult@(n -
n/2)(a, c);
int@(2 ∗ (n/2)) t2 = karatsubaMult@(n/2)(b, d);
int@(n - n/2 + 1) aPb = a + b;
int@(n - n/2 + 1) cPd = c + d;
50 / 82

int@(2 ∗ (n - n/2 + 1)) t3 = karatsubaMult@(n -
n/2 + 1)(aPb, cPd);
int@(2 ∗ n) padt1 = t1;
int@(2 ∗ n) padt2 = t2;
int@(2 ∗ n) padt3 = t3;
ret = (padt1<<(n) + padt2 + ((padt3 - padt1
- padt2)<<(n/2)); }
return ret; }
51 / 82

Outline
1 Acknowledgement
2 Introduction
Overview
Programmer’s View
Features
Standard Types
Generic Types
Native Types
Loop Coalescing
4 Applications
MapReduce
Circuit ORAM
Stack
Dijkstra Algorithm
5 ObliVM Compiler
Compilation Process
Execution Process
Input Preparation
6 Results
Input Preparation
Compilation
Execution
7 Summary
8 References
52 / 82

Stack
Stack is one of the linear and homogeneous data structures, works on
LIFO (Last In Fast Out) principle.
Elements are inserted at stack Top, called Push operation.
Elements are removed from stack Top, called Pop operation.
Figure 4.2: Stack data structure
53 / 82

Stack
Circuit ORAM Operations
rnd@m RND(public int32 m) = native lib.rand;
struct Pointer@m {
int32 index;
rand@m pos; };
struct SecStore@m<T> {
CircuitORAM@m<T> oram;
int32 cnt; };
phantom void SecStore@m<T>.add(int32 index, int@m pos, T
data) {
oram.add(index, pos, data); }
54 / 82

Stack
Circuit ORAM Operations
phantom T SecStore@m<T>.readAndRemove(int32 index, rnd@m
pos) {
return oram.readAndRemove(index, pos); }
phantom Pointer@m SecStore@m<T>.allocate() {
cnt = cnt + 1;
return Pointer@m(cnt, RND(m)); }
readAndRemove(...) is used to read an element using circuit
ORAM. allocate(...) is used to assigned new path to read
element.
add(...) is used to write the element in new path.
Above functions are called inside stack to implement push and pop
operations. Normally, used by non-specialist programmer.
55 / 82

Stack
Oblivious Stack
struct StackNode@m<T> {
Pointer@m next;
T data; };
struct Stack@m<T> {
Pointer@m top;
SecStore@m store; };
phantom void Stack@m<T>.push(T data) {
StackNode@m<T> node = StackNode@m<T> (top, data);
this.top = this.store.allocate();
store.add(top.index, top.pos, node); }
phantom T Stack@m<T>.pop() {
StackNode@m<T> res = store.readAndRemove(top.index,
top.pos);
top = res.next;
return res.data; }
56 / 82

Outline
1 Acknowledgement
2 Introduction
Overview
Programmer’s View
Features
Standard Types
Generic Types
Native Types
Loop Coalescing
4 Applications
MapReduce
Circuit ORAM
Stack
Dijkstra Algorithm
5 ObliVM Compiler
Compilation Process
Execution Process
Input Preparation
6 Results
Input Preparation
Compilation
Execution
7 Summary
8 References
57 / 82

Dijkstra Algorithm
One of the single source shortest path algorithm used to ﬁnd shortest
distance for other nodes from a given node.
It has lots of applications. Routing protocols (OSPF and IS-IS) use
Dijkstra as backbone.
Figure 4.3: Shortest path from node ’1’ using Dijkstra.
58 / 82

Dijkstra Algorithm
Given Input Secrets: Source node ’s’, Adjacency list ’e’ and sum of out
degrees s[u].
1: Initialize dis = [∞, ∞, ∞, .....,∞] and dis[s] = 0
2: PQ.push(0, s)
3: while (!PQ.empty())
4: (dist, u) = PQ.deleteMin()
5: if (dist == dis[u])
6: dis[u] = -dis[u]
7: for (i = s[u]; i < s[u+1]; i++)
8: (u, v, w) = e[i]
9: newDist = dist + w
10: if (newDist < dis[v])
11: dis[v] = newDist
12: PQ.insert(newDist, v)
59 / 82

Dijkstra Algorithm
Oblivious Dijkstra with Loop Coalescing
Input Secrets: Source ’s’, Adjacency list ’e’ and Sum of Out-degrees s[u].
1: Initialize dis = [∞, .....,∞] and dis[s] = 0, innerLoop = False
2: PQ.push(0, s)
3: for (i = 0 → 2V + E - 1)
4: (dist, u) = PQ.deleteMin()
5: if (dist == dis[u])
6: dis[u] = -dis[u], i = s[u], innerLoop = True
7: else
8: if i < s[u+1]
9: (u, v, w) = e[i], newDist = dist + w
10: if newDist < dis[v]
11: dis[v] = newDist, PQ.insert(newDist, v)
12: i = i + 1
13: else
14: innerLoop = False
60 / 82

Outline
1 Acknowledgement
2 Introduction
Overview
Programmer’s View
Features
Standard Types
Generic Types
Native Types
Loop Coalescing
4 Applications
MapReduce
Circuit ORAM
Stack
Dijkstra Algorithm
5 ObliVM Compiler
Compilation Process
Execution Process
Input Preparation
6 Results
Input Preparation
Compilation
Execution
7 Summary
8 References
61 / 82

Prerequisite for Ubuntu
Install python 2.7: sudo apt-get install python
Install Oracle Java 8 JavaCC 5.0
sudo apt-add-repository ppa:webupd8team/java
sudo apt-get update
sudo apt-get install oracle-java8-installer
java -version
Download ’ObliVM’ from this URL
https://github.com/oblivm/ObliVMLang
Prepare ObliVM environment: ./compile.sh
62 / 82

Outline
1 Acknowledgement
2 Introduction
Overview
Programmer’s View
Features
Standard Types
Generic Types
Native Types
Loop Coalescing
4 Applications
MapReduce
Circuit ORAM
Stack
Dijkstra Algorithm
5 ObliVM Compiler
Compilation Process
Execution Process
Input Preparation
6 Results
Input Preparation
Compilation
Execution
7 Summary
8 References
63 / 82

Compilation Process
Figure 5.1: ObliVM compilation process
ObliVM compiler converts Source code (.lcc file) to a set of .java files.
Javac Compiler converts those to byte codes (.class files).
run-compiler.sh command is used to convert .lcc to .java.
Example: ./run-compiler.sh 54321
examples/millionare/millionare.lcc
64 / 82

Compilation Process
run-compiler.sh ﬁle contains the following commands
1 mkdir -p flexsc-bin;
2 mkdir -p to-run;
3 java -cp bin:lib/* com.oblivm.compiler.cmd.Cmd -o
./flexsc-bin/ -p 12;
4 find flexsc-bin -name "*.java">source.txt;
5 javac -cp to-run:lib/* -d to-run @source.txt;
65 / 82

Compilation Process
Figure 5.2: Front end compilation
The ﬁrst three commands are come under front end compilation.
1 mkdir -p flexsc-bin;
2 mkdir -p to-run;
3 java -cp bin:lib/* com.oblivm.compiler.cmd.Cmd -o
./flexsc-bin/ -p 12;
66 / 82

Compilation Process
Figure 5.3: Back end code generation.
The last two commands are come under back end code generation.
1 find flexsc-bin -name "*.java">source.txt;
2 javac -cp to-run:lib/* -d to-run @source.txt;
67 / 82

Outline
1 Acknowledgement
2 Introduction
Overview
Programmer’s View
Features
Standard Types
Generic Types
Native Types
Loop Coalescing
4 Applications
MapReduce
Circuit ORAM
Stack
Dijkstra Algorithm
5 ObliVM Compiler
Compilation Process
Execution Process
Input Preparation
6 Results
Input Preparation
Compilation
Execution
7 Summary
8 References
68 / 82

Execution Process
Final byte codes (.class files) with two files are given as input to JVM
interpreter to generate final output.
countConfig.conf and Cmd.class files are linked to generate final
output.
runtogether.sh command is used to execute the byte code. It
contains the following commands.
java -cp to-run:lib/* com.oblivm.backend.lang.inter.Cmd
-t eva -i $2 -config countConfig.conf -c
com.oblivm.backend.generated.millionare.NoClass & java
-cp to-run:lib/* com.oblivm.backend.lang.inter.Cmd -t
gen -i $1 -config countConfig.conf -c
com.oblivm.backend.generated.millionare.NoClass
69 / 82

Outline
1 Acknowledgement
2 Introduction
Overview
Programmer’s View
Features
Standard Types
Generic Types
Native Types
Loop Coalescing
4 Applications
MapReduce
Circuit ORAM
Stack
Dijkstra Algorithm
5 ObliVM Compiler
Compilation Process
Execution Process
Input Preparation
6 Results
Input Preparation
Compilation
Execution
7 Summary
8 References
70 / 82

Input Preparation
Input files to ObliVM contains binary strings.
datainitializer.py from tools folder is used to generate final
input files from raw input files.
71 / 82

Outline
1 Acknowledgement
2 Introduction
Overview
Programmer’s View
Features
Standard Types
Generic Types
Native Types
Loop Coalescing
4 Applications
MapReduce
Circuit ORAM
Stack
Dijkstra Algorithm
5 ObliVM Compiler
Compilation Process
Execution Process
Input Preparation
6 Results
Input Preparation
Compilation
Execution
7 Summary
8 References
72 / 82

Input Preparation
Examples: Find maximum within a set of numbers.
Alice Raw Input (input raw alice.txt): 1 3 5 7
Bob Raw Input (input raw bob.txt): 17
Alice ﬁnal Input (input bin alice.txt): 1000000000000000000000
00000000001100000000000000000000000000000010100000000
00000000000000000000011100000000000000000000000000000
Bob ﬁnal Input (input bin bob.txt): 10001000000000000000000
000000000
Note: Binary value of 17 is 10001, appended with 0000000000
00000000000000000. Total 32 bits.
73 / 82

Outline
1 Acknowledgement
2 Introduction
Overview
Programmer’s View
Features
Standard Types
Generic Types
Native Types
Loop Coalescing
4 Applications
MapReduce
Circuit ORAM
Stack
Dijkstra Algorithm
5 ObliVM Compiler
Compilation Process
Execution Process
Input Preparation
6 Results
Input Preparation
Compilation
Execution
7 Summary
8 References
74 / 82

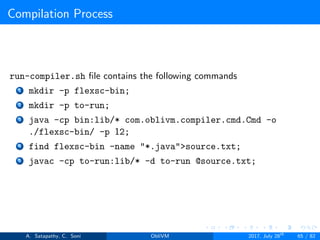
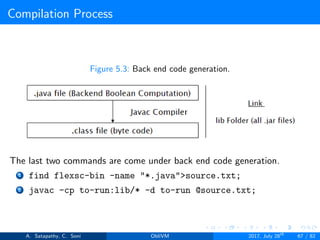
Compilation
Find the maximum within set of numbers without using Trivial ORAM.
File location: examples/ﬁndmax3.lcc
1: package com.oblivm.backend.generated.findmax;
2: int main@n(int[public n] x, int y) {
3: int max = y;
4: for(public int i = 0; i<n; i = i + 1) {
5: if (x[i] > max) max = x[i];
6: }
7: return max;
8: }
Compilation: ./run-compiler.sh 54321 examples/findmax/
findmax3.lcc
75 / 82

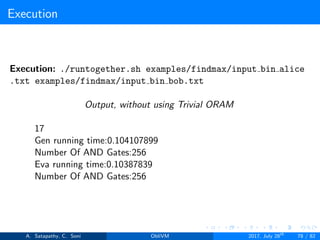
Compilation
Find the maximum within set of numbers using Trivial ORAM.
File location: examples/ﬁndmax2.lcc
1: package com.oblivm.backend.generated.findmax;
2: int main@n(int[n] x, int y) {
3: int max = y;
4: bfor (n) (int i = 0; i<n; i = i + 1) {
5: if (x[i] > max) max = x[i];
6: }
7: return max;
8: }
Compilation: ./run-compiler.sh 54321 examples/findmax/
findmax2.lcc
76 / 82

Outline
1 Acknowledgement
2 Introduction
Overview
Programmer’s View
Features
Standard Types
Generic Types
Native Types
Loop Coalescing
4 Applications
MapReduce
Circuit ORAM
Stack
Dijkstra Algorithm
5 ObliVM Compiler
Compilation Process
Execution Process
Input Preparation
6 Results
Input Preparation
Compilation
Execution
7 Summary
8 References
77 / 82

Execution
Execution: ./runtogether.sh examples/findmax/input bin alice
.txt examples/findmax/input bin bob.txt
Output, without using Trivial ORAM
17
Gen running time:0.104107899
Number Of AND Gates:256
Eva running time:0.10387839
78 / 82

Execution
Execution: ./runtogether.sh examples/findmax/input bin alice
.txt examples/findmax/input bin bob.txt
Output, using Trivial ORAM
17
Eva running time:0.13543389
Gen running time:0.118504565
79 / 82

Summary
We discussed
1 ObliVM framework and its data types and functions.
2 Implicit declassifications, function trace, phantom function and loop
coalescing technique.
3 Oblivious implementation of different algorithms such as MapReduce,
circuit ORAM, Karatsuba multiplication etc.
4 Environment installation, data preparation, compilation and execution.
5 pre-implemented findmax programs with results.
80 / 82

References
C. Liu et al., ”ObliVM: A Programming Framework for Secure
Computation”, in IEEE Symposium on Security and Privacy (S&P),
2015.
”oblivm/ObliVMLang”, GitHub, 2017. [Online]. Available:
https://github.com/oblivm/ObliVMLang. [Accessed: 05- Jun- 2017].
81 / 82

The End
82 / 82

ObliVM

More Related Content

What's hot

Similar to ObliVM

More from Ashutosh Satapathy

Recently uploaded

ObliVM