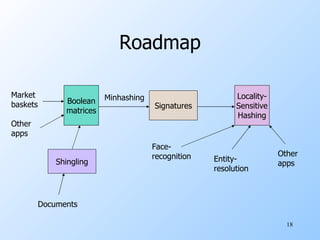
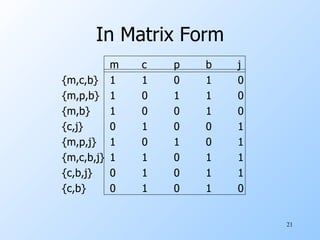
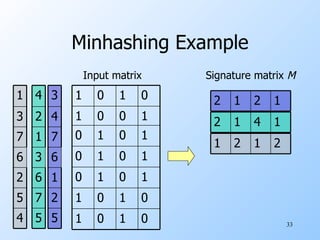
This document discusses techniques for efficiently finding similar items in large datasets, including near-neighbor search, entity resolution, and document similarity. It introduces the concept of minhashing as a method to represent datasets in a way that allows efficient comparison of similarities. Minhashing works by using hash functions to map items to signatures in a way that preserves estimates of Jaccard similarity between items.

1. Near-Neighbor Search Applications Matrix Formulation Minhashing

2. Example Problem --- Face Recognition We have a database of (say) 1 million face images. We are given a new image and want to find the most similar images in the database. Represent faces by (relatively) invariant values, e.g., ratio of nose width to eye width.

3. Face Recognition --- (2) Each image represented by a large number (say 1000) of numerical features. Problem : given the features of a new face, find those in the DB that are close in at least ¾ (say) of the features.

4. Face Recognition --- (3) Many-one problem : given a new face, see if it is close to any of the 1 million old faces. Many-Many problem : which pairs of the 1 million faces are similar.

5. Simple Solution Represent each face by a vector of 1000 values and score the comparisons. Sort-of OK for many-one problem. Out of the question for the many-many problem (10 6 *10 6 *1000 numerical comparisons). We can do better !

6. Multidimensional Indexes Don’t Work New face: [6,14,…] 0-4 5-9 10-14 . . . Dimension 1 = Surely we’d better look here. Maybe look here too, in case of a slight error. But the first dimension could be one of those that is not close. So we’d better look everywhere!

7. Another Problem : Entity Resolution Two sets of 1 million name-address-phone records. Some pairs, one from each set, represent the same person. Errors of many kinds : Typos, missing middle initial, area-code changes, St./Street, Bob/Robert, etc., etc.

8. Entity Resolution --- (2) Choose a scoring system for how close names are. Deduct so much for edit distance > 0; so much for missing middle initial, etc. Similarly score differences in addresses, phone numbers. Sufficiently high total score -> records represent the same entity.

9. Simple Solution Compare each pair of records, one from each set. Score the pair. Call them the same if the score is sufficiently high. Unfeasible for 1 million records. We can do better !

10. Yet Another Problem : Finding Similar Documents Given a body of documents, e.g., the Web, find pairs of docs that have a lot of text in common. Find mirror sites, approximate mirrors, plagiarism, quotation of one document in another, “good” document with random spam, etc.

11. Complexity of Document Similarity The face problem had a way of representing a big image by a (relatively) small data-set. Entity records represent themselves. How do you represent a document so it is easy to compare with others ?

12. Complexity --- (2) Special cases are easy, e.g., identical documents, or one document contained verbatim in another. General case, where many small pieces of one doc appear out of order in another, is very hard.

13. Representing Documents for Similarity Search Represent doc by its set of shingles (or k -grams). Summarize shingle set by a signature = small data-set with the property: Similar documents are very likely to have “similar” signatures. At that point, doc problem resembles the previous two problems.

14. Shingles A k -shingle (or k -gram ) for a document is a sequence of k characters that appears in the document. Example : k=2; doc = abcab. Set of 2-shingles = {ab, bc, ca}. Option : regard shingles as a bag, and count ab twice.

15. Shingles: Aside Although we shall not discuss it, shingles are a powerful tool for characterizing the topic of documents. k =5 is the right number; (#characters) 5 >> # shingles in typical document. Example : “ng av” and “ouchd” are most common in sports articles.

16. Shingles: Compression Option To compress long shingles, we can hash them to (say) 4 bytes. Represent a doc by the set of hash values of its k -shingles. Two documents could (rarely) appear to have shingles in common, when in fact only the hash-values were shared.

17. MinHashing Data as Sparse Matrices Jaccard Similarity Measure Constructing Signatures

18. Roadmap Boolean matrices Market baskets Other apps Signatures Locality- Sensitive Hashing Minhashing Face- recognition Entity- resolution Other apps Shingling Documents

19. Boolean Matrix Representation Data in the form of subsets of a universal set can be represented by a (typically sparse) matrix. Examples include: Documents represented by their set of shingles (or hashes of those shingles). Market baskets.

20. Matrix Representation of Item/Basket Data Columns = items. Rows = baskets. Entry ( r , c ) = 1 if item c is in basket r ; = 0 if not. Typically matrix is almost all 0’s.

21. In Matrix Form m c p b j {m,c,b} 1 1 0 1 0 {m,p,b} 1 0 1 1 0 {m,b} 1 0 0 1 0 {c,j} 0 1 0 0 1 {m,p,j} 1 0 1 0 1 {m,c,b,j} 1 1 0 1 1 {c,b,j} 0 1 0 1 1 {c,b} 0 1 0 1 0

22. Documents in Matrix Form Columns = documents. Rows = shingles (or hashes of shingles). 1 in row r , column c iff document c has shingle r . Again expect the matrix to be sparse.

23. Aside We might not really represent the data by a boolean matrix. Sparse matrices are usually better represented by the list of places where there is a non-zero value. E.g., baskets, shingle-sets. But the matrix picture is conceptually useful.

24. Assumptions Number of items allows a small amount of main-memory/item. E.g., main memory = Number of items * 100 2. Too many items to store anything in main-memory for each pair of items.

25. Similarity of Columns Think of a column as the set of rows in which it has 1. The similarity of columns C 1 and C 2 = Sim (C 1 ,C 2 ) = is the ratio of the sizes of the intersection and union of C 1 and C 2 . Sim (C 1 ,C 2 ) = |C 1  C 2 |/|C 1  C 2 | = Jaccard measure .

26. Example C 1 C 2 0 1 1 0 1 1 Sim (C 1 , C 2 ) = 0 0 2/5 = 0.4 1 1 0 1 * * * * * * *

27. Outline of Algorithm Compute signatures of columns = small summaries of columns. Read from disk to main memory. Examine signatures in main memory to find similar signatures. Essential : similarities of signatures and columns are related. Optional : check that columns with similar signatures are really similar.

28. Warnings Comparing all pairs of signatures may take too much time, even if not too much space. A job for Locality-Sensitive Hashing. These methods can produce false negatives, and even false positives if the optional check is not made.

29. Signatures Key idea : “hash” each column C to a small signature Sig (C), such that: 1. Sig (C) is small enough that we can fit a signature in main memory for each column. Sim (C 1 , C 2 ) is the same as the “similarity” of Sig (C 1 ) and Sig (C 2 ).

30. An Idea That Doesn’t Work Pick 100 rows at random, and let the signature of column C be the 100 bits of C in those rows. Because the matrix is sparse, many columns would have 00. . .0 as a signature, yet be very dissimilar because their 1’s are in different rows.

31. Four Types of Rows Given columns C 1 and C 2 , rows may be classified as: C 1 C 2 a 1 1 b 1 0 c 0 1 d 0 0 Also, a = # rows of type a , etc. Note Sim (C 1 , C 2 ) = a /( a + b + c ).

32. Minhashing Imagine the rows permuted randomly. Define “hash” function h ( C ) = the number of the first (in the permuted order) row in which column C has 1. Use several (100?) independent hash functions to create a signature.

33. Minhashing Example Input matrix 0 1 0 1 0 1 0 1 1 0 1 0 1 0 1 0 1 0 1 0 1 0 0 1 0 1 0 1 5 2 1 6 7 4 3 Signature matrix M 1 2 1 2 5 7 6 3 1 2 4 1 4 1 2 4 5 2 6 7 3 1 2 1 2 1

34. Surprising Property The probability (over all permutations of the rows) that h (C 1 ) = h (C 2 ) is the same as Sim (C 1 , C 2 ). Both are a /( a + b + c )! Why ? Look down columns C 1 and C 2 until we see a 1. If it’s a type- a row, then h (C 1 ) = h (C 2 ). If a type- b or type- c row, then not.

35. Similarity for Signatures The similarity of signatures is the fraction of the rows in which they agree. Remember, each row corresponds to a permutation or “hash function.”

36. Min Hashing – Example Similarities: 1-3 2-4 1-2 3-4 Col/Col 0.75 0.75 0 0 Sig/Sig 0.67 1.00 0 0 Input matrix 0 1 0 1 0 1 0 1 1 0 1 0 1 0 1 0 1 0 1 0 1 0 0 1 0 1 0 1 5 2 1 6 7 4 3 Signature matrix M 1 2 1 2 5 7 6 3 1 2 4 1 4 1 2 4 5 2 6 7 3 1 2 1 2 1

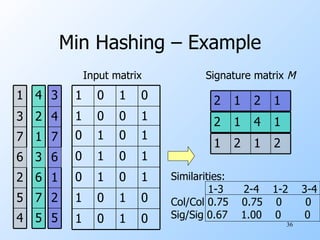
37. Minhash Signatures Pick (say) 100 random permutations of the rows. Think of Sig (C) as a column vector. Let Sig (C)[i] = according to the i th permutation, the number of the first row that has a 1 in column C .

38. Implementation --- (1) Number of rows = 1 billion (say). Hard to pick a random permutation from 1…billion. Representing a random permutation requires 1 billion entries. Accessing rows in permuted order is tough! The number of passes would be prohibitive.

39. Implementation --- (2) Pick (say) 100 hash functions. For each column c and each hash function h i , keep a “slot” M ( i, c ) for that minhash value.

40. Implementation --- (3) for each row r for each column c if c has 1 in row r for each hash function h i do if h i ( r ) is a smaller value than M ( i, c ) then M ( i, c ) := h i ( r ) Needs only one pass through the data.

41. Example Row C1 C2 1 1 0 2 0 1 3 1 1 4 1 0 5 0 1 h ( x ) = x mod 5 g ( x ) = 2 x +1 mod 5 h (1) = 1 1 - g (1) = 3 3 - h (2) = 2 1 2 g (2) = 0 3 0 h (3) = 3 1 2 g (3) = 2 2 0 h (4) = 4 1 2 g (4) = 4 2 0 h (5) = 0 1 0 g (5) = 1 2 0 Sig1 Sig2