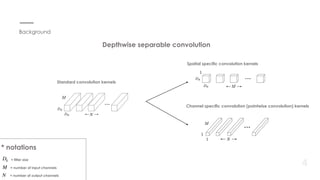
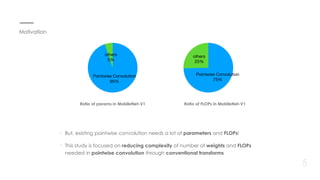
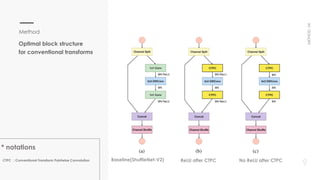
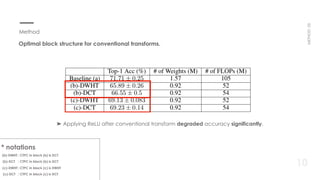
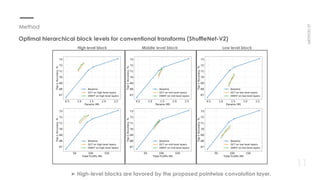
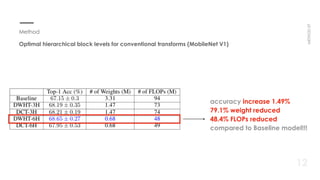
This document proposes a new method for pointwise convolution in deep neural networks using conventional transforms like discrete cosine transform (DCT) and discrete Walsh-Hadamard transform (DWHT) to reduce complexity. It presents 7 key aspects of the method: 1) Using DCT and DWHT kernels for pointwise convolution without learnable parameters; 2) The transforms are fast to compute; 3) An optimal block structure applies transforms between blocks; 4) Adding ReLU after transforms degrades accuracy; 5) Evaluating DCT-DCT and DCT-DWHT block combinations; 6) Determining optimal hierarchical levels to apply the transforms; 7) The method increases accuracy while reducing weights and FLOPs compared to baselines.