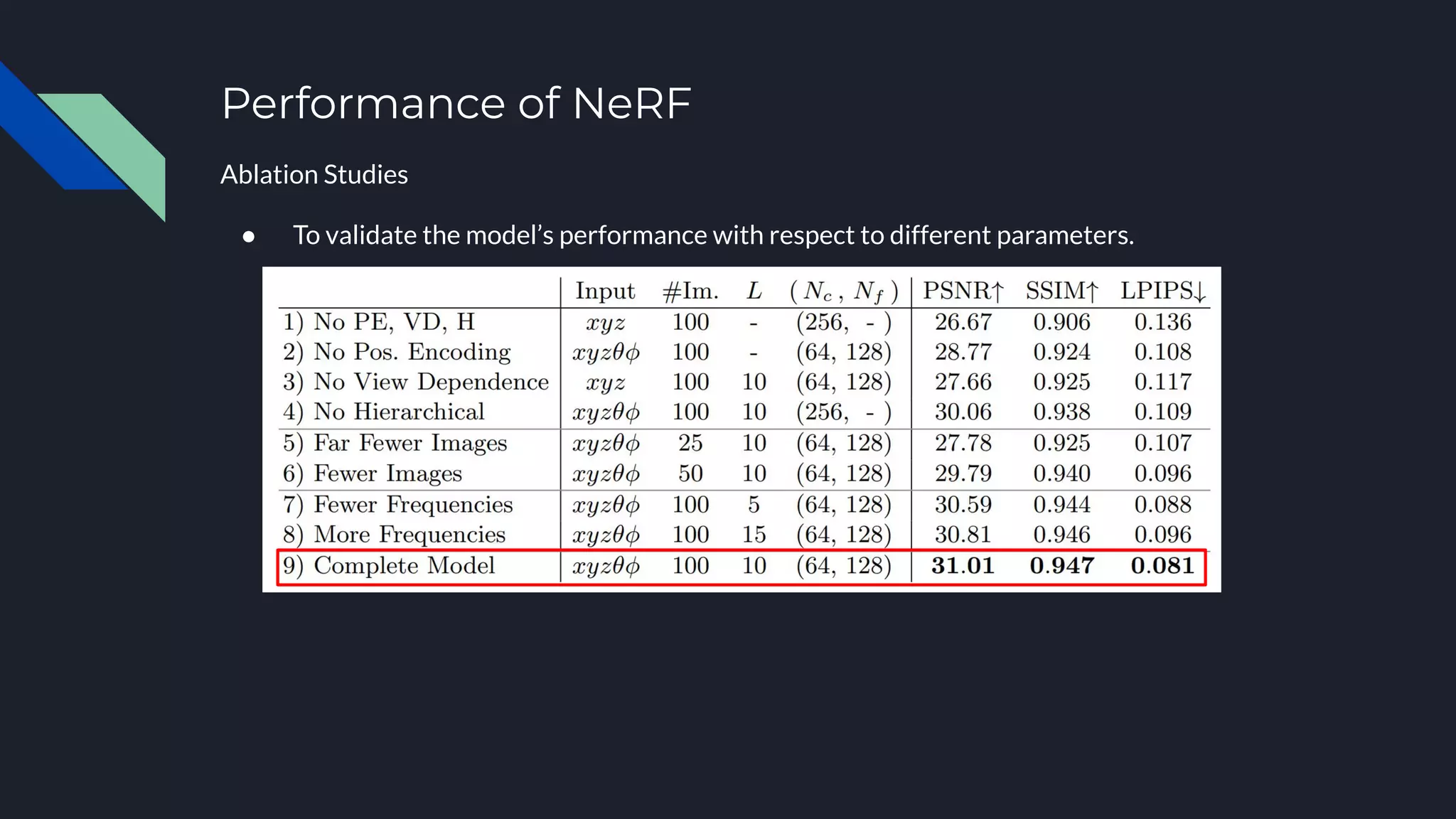
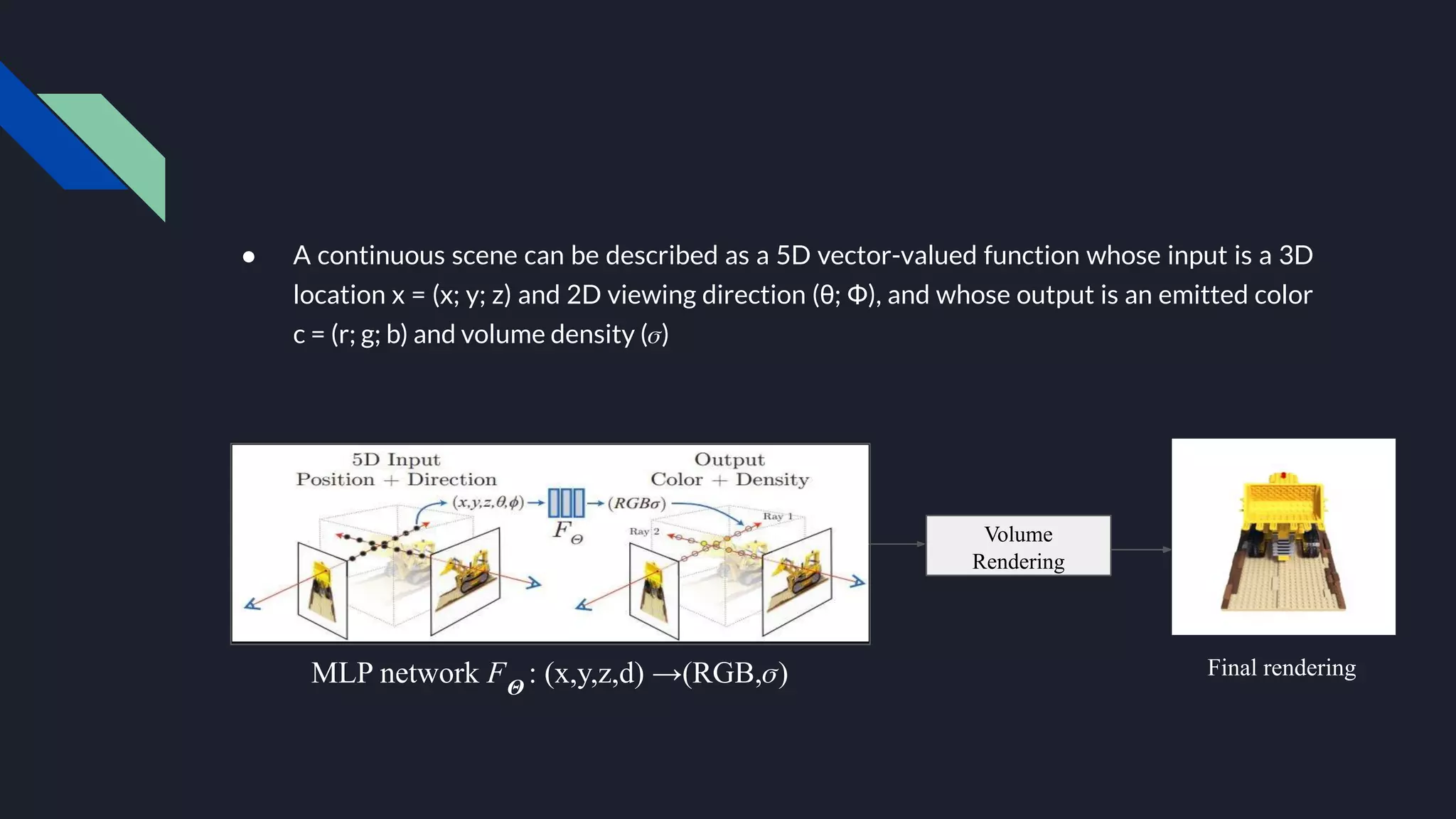
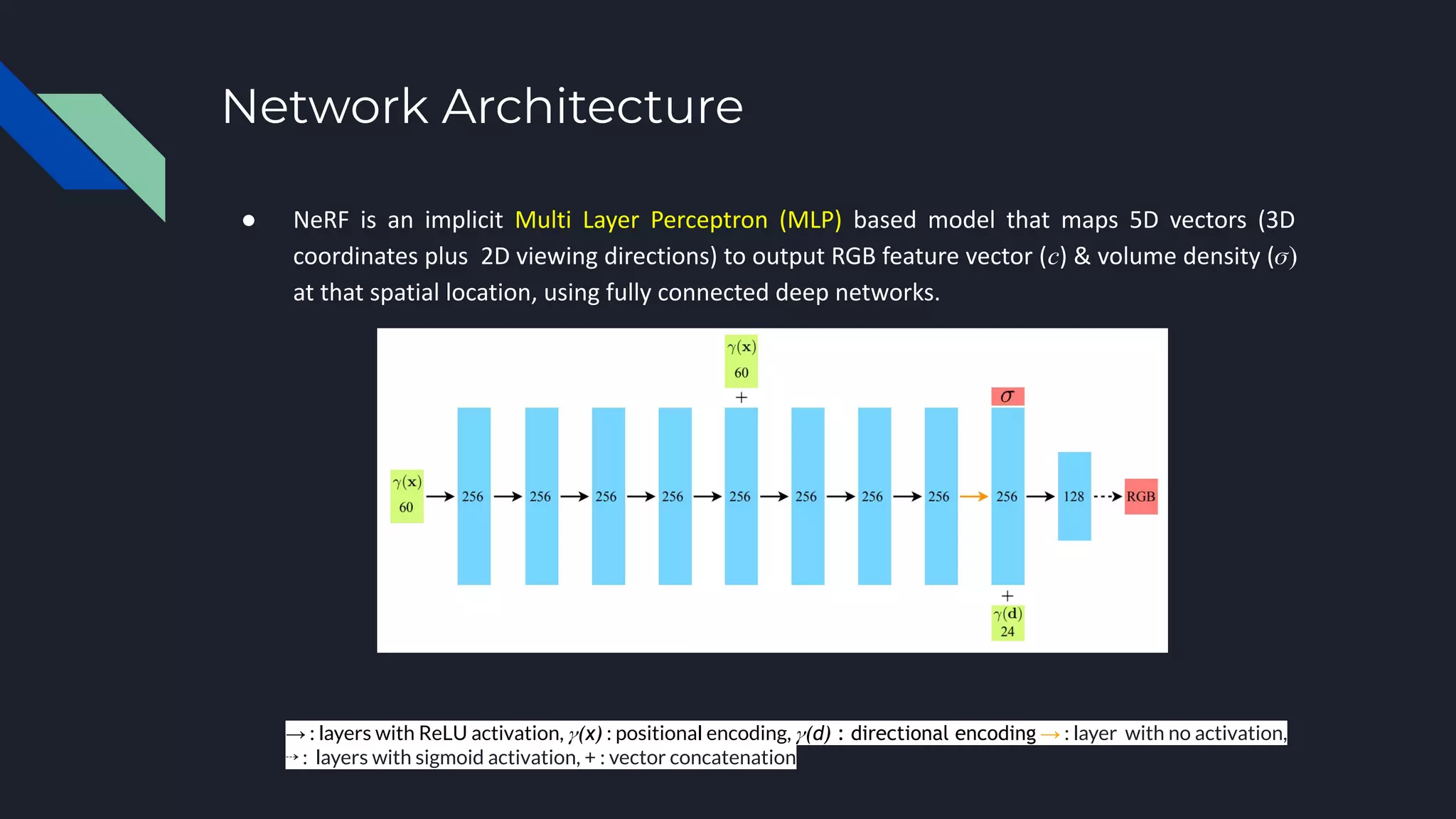
Neural Radiance Fields (NeRF) represents scenes as neural radiance fields that can be used for novel view synthesis. NeRF learns a continuous radiance field from a sparse set of input views using a multi-layer perceptron that maps 5D coordinates to RGB color and density values. It uses volumetric rendering to integrate these values along camera rays and optimizes the network via differentiable rendering and a reconstruction loss. NeRF produces high-fidelity novel views and has inspired extensions like handling dynamic scenes and reconstructing scenes from unstructured internet photos.

1. Neural Radiance Fields
& Neural Rendering
Mildenhall, Ben, et al. "Nerf: Representing scenes as neural radiance fields
for view synthesis." Communications of the ACM 65.1 (2021): 99-106.
Navneet Paul
PlayerUnknown Productions

2. Rendering
● Process of generating an image from a 2D or 3D model using a computer program. The
resulting image is called render.
● A rendering application takes into account inputs such as the model (2D/3D), texture,
shading, lighting, viewpoints, etc, as features during the rendering process.
● It means we can say that each scene file contains multiple features that need to be
understood and processed by the rendering algorithm or application to generate a
processed image.

3. Rendering Equation
● The rendering algorithm or technique which tries to solve the problem of image
generation based on all given features is mostly trying to optimize the rendering equation.
● At a high-level the rendering equation computes for a radiance that is illumination
(reflection, refraction, and emittance of light) on an object from a source to an observer in
a given space.
● NeRF essentially computes for the Volume Rendering.

4. Volume Rendering
● Volume rendering (as per Wikipedia) is a set of a technique used to display a 2D projection of a
3D discretely sampled dataset.
● To render a 2D projection (output) of a 3D dataset we first need to define the camera position in
space relative to the volume then we need to define the RGBα (Red, Green. Blue, Alpha → it
stands for opacity channel) for every voxel.
● The primary objective in volume rendering is to get a transfer function which defines RGBα for
every value for every possible voxel value in a given space.

5. View Synthesis
● Click photos of an object from multiple camera angles and superimpose the images to
have a look at the same object from different known camera angles and positions.
● For NeRF, we are trying to predict the third missing axis (the first two being length &
breadth) which is the depth.
● Core application of NeRF: to predict a function for depth determination at various points
in the plane against the object itself.

6. Neural Radiance Fields
● Generate novel views of complex scenes by optimizing an underlying continuous
volumetric scene function using a sparse set of input views.
● The input can be provided as a blender model or a static set of images.
● The input is provided as a continuous 5D function that outputs the radiance emitted in
each direction (θ; Φ) at each point (x; y; z) in space, and a density at each point which
acts like a differential opacity controlling how much radiance is accumulated by a ray
passing through (x; y; z)

7. ● A continuous scene can be described as a 5D vector-valued function whose input is a 3D
location x = (x; y; z) and 2D viewing direction (θ; Φ), and whose output is an emitted color
c = (r; g; b) and volume density (𝜎)
Volume
Rendering
Final rendering
MLP network F𝚯
: (x,y,z,d) →(RGB,𝜎)

8. Process overview
To generate a Neural Radiance Field from a particular viewpoint following steps were done:
● March camera rays through the scene to generate a sampled set of 3D points (Use either
COLMAP* or SfM for generating camera poses and viewing directions).
● Use those points and their corresponding 2D viewing directions as input to the neural network to
produce an output set of colors (RGB) and densities (𝜎)
● Use classical volume rendering approach to accumulate those colors and densities into a 2D
image
* a general-purpose Structure-from-Motion (SfM) and Multi-View Stereo (MVS) pipeline with a graphical and command-line interface

9. Network Architecture
● NeRF is an implicit Multi Layer Perceptron (MLP) based model that maps 5D vectors (3D
coordinates plus 2D viewing directions) to output RGB feature vector (c) & volume density (𝜎)
at that spatial location, using fully connected deep networks.
→ : layers with ReLU activation, 𝛾(x) : positional encoding, 𝛾(d) : directional encoding → : layer with no activation,
⇢ : layers with sigmoid activation, + : vector concatenation

10. Volume Rendering
● The authors used discrete data samples to estimate the expected color C(r) of camera ray r(t) with
the quadrature rule in classical volume rendering techniques.
Predicted colors
Volume density
Opacity

11. NeRF Optimization - Positional Encoding
● Previous studies show that optimizing the inputs to a higher dimensional space using high frequency functions
before passing them to the network enables better fitting of data that contains high frequency variation.
● Positional & Directional Encoding: A Fourier based feature mapping function that encodes features (pertaining
to position & direction) from lower dimensional space to a higher dimensional space.
Positional Encoding func.
Tancik, Srinivasan, Mildenhall et al., Fourier Features Let Networks Learn High Frequency
Functions in Low Dimensional Domains, NeurIPS 2020
No
Positional
Encoding
With
Positional
Encoding

12. NeRF Optimization - Hierarchical Sampling
● During the volume rendering phase, our model simultaneously optimizes two networks: coarse and fine
● We first sample a set of NC
locations with the RGB feature vector and density [σ (t)] outputs from the proposed
NeRF model, using stratified sampling, and evaluate the “coarse” network at these locations.
● The main function of coarse network is to compute the final rendered color of the ray for the coarse samples.
● a second set of Nf
locations are sampled from the [RGB + density] distribution using inverse transform sampling &
evaluate our “fine” network.
● All the samples are considered while computing the final rendered ray color, i.e, (NC
+ Nf
), at fine network stage.
This is done to ensure that more samples are allocated to regions we expect to contain visible content.

13. Final Rendering & Loss Function
● Optimize a separate neural continuous volume representation network, for each scene.
● At each optimization iteration, we randomly sample a batch of camera rays from the set of
all pixels in the dataset, and then follow the hierarchical sampling.
● NC
samples from the coarse network and NC
+ Nf
samples from the fine network.
● We then use the volume rendering procedure to render the color of each ray from both
sets of samples.
● Loss function is based on the the total squared error between the rendered and true pixel
colors for both the coarse and fine samples.
ℛ: set of rays in each batch; C(r): ground truth, ĈC
(r): coarse volume prediction and Ĉf
(r): fine volume prediction for RGB colors for ray “r”

14. Performance of NeRF
Comparison to other view synthesis techniques
● Neural Volumes, Local Light Field Fusion (LLFF)
& Scene Representation Networks (SRN
(Ours = NeRF)

15. Performance of NeRF
Ablation Studies
● To validate the model’s performance with respect to different parameters.

16. Summary
● Learn the radiance field of a scene based on a
collection of calibrated images
○ Use an MLP to learn continuous
geometry and view-dependent
appearance
● Use fully differentiable volume rendering with
reconstruction loss
● Combines hierarchical sampling and
Fourier-based encoding of 5D inputs to produce
high-fidelity novel view synthesis results
Some associated challenges
● Handling dynamic scenes when acquiring
calibrated views
● One network trained per scene - no
generalization

17. Related NeRF Research
● NeRF in Wild: a novel approach for 3D scene reconstruction of complex environments from unstructured
internet photo collections that incorporates transient and latent scene embedding upon conventional NeRF
model.
*Martin-Brualla, Ricardo, et al. "Nerf in the wild: Neural radiance fields for unconstrained photo collections." Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2021.
● The model captures lighting and photometric variations in a low-dimensional latent embedding space in
rendering appearance without affecting 3D geometry.

18. ● Neural Radiance Fields for Dynamic Scenes : for synthesizing novel views, at an arbitrary point in
time, of dynamic scenes with complex non-rigid geometries.
● Optimize an underlying deformable volumetric function (using a deformation network) from a sparse set
of input monocular views without the need of ground-truth geometry nor multi-view images
Pumarola, Albert, et al. "D-nerf: Neural radiance fields for dynamic scenes." Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2021.
Related NeRF Research