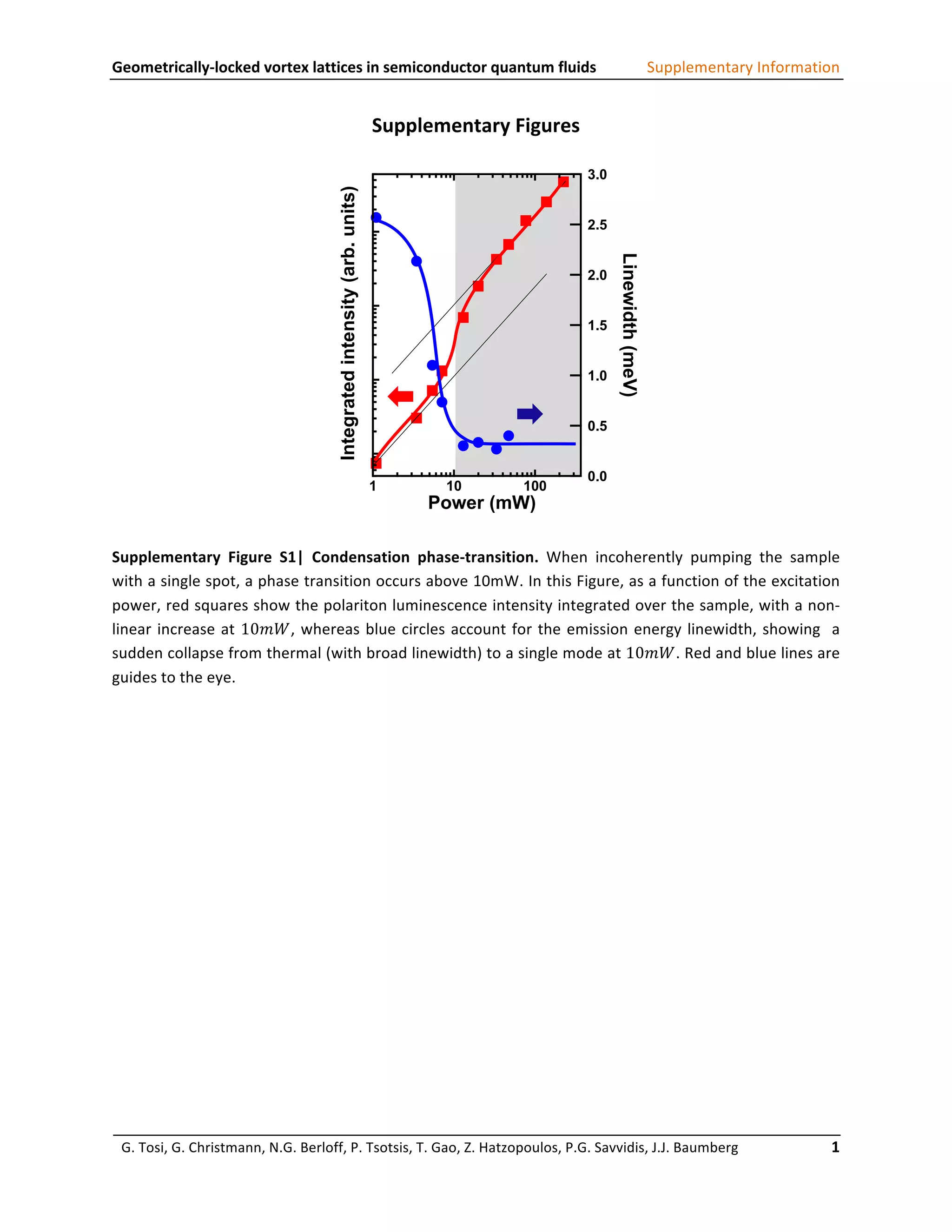
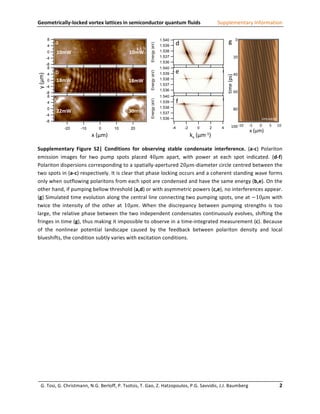
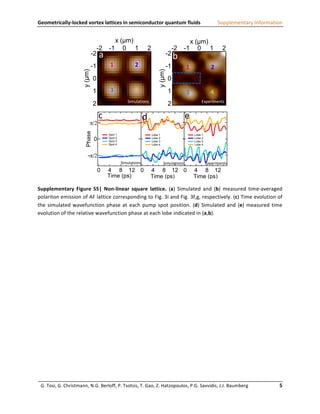
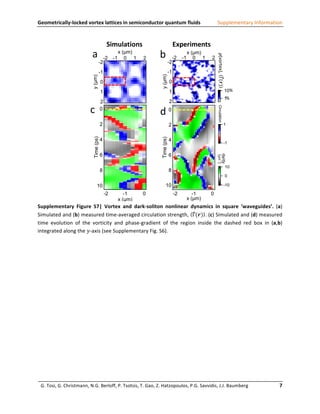
This document provides supplementary information to support a study on geometrically-locked vortex lattices in semiconductor quantum fluids. Figure S1 shows experimental data on the condensation phase transition that occurs in the quantum fluid above 10 mW of pumping power. Figure S2 demonstrates the conditions needed to observe stable interference between condensates from two pump spots, including the requirement that they have the same energy level. Figure S3 simulates the hexagonal lattice wavefunction that arises from the interference pattern. Figure S4 shows simulations of ordered square lattices that can form from interference between four plane waves.

1. Geometrically-­‐locked
vortex
lattices
in
semiconductor
quantum
fluids
Supplementary
Information
Supplementary
Figures
3.0
Integrated intensity (arb. units)
2.5
Linewidth (meV)
2.0
1.5
1.0
0.5
0.0
1 10 100
Power (mW)
Supplementary
Figure
S1|
Condensation
phase-­‐transition.
When
incoherently
pumping
the
sample
with
a
single
spot,
a
phase
transition
occurs
above
10mW.
In
this
Figure,
as
a
function
of
the
excitation
power,
red
squares
show
the
polariton
luminescence
intensity
integrated
over
the
sample,
with
a
non-­‐
linear
increase
at
10𝑚𝑊,
whereas
blue
circles
account
for
the
emission
energy
linewidth,
showing
a
sudden
collapse
from
thermal
(with
broad
linewidth)
to
a
single
mode
at
10𝑚𝑊.
Red
and
blue
lines
are
guides
to
the
eye.
G.
Tosi,
G.
Christmann,
N.G.
Berloff,
P.
Tsotsis,
T.
Gao,
Z.
Hatzopoulos,
P.G.
Savvidis,
J.J.
Baumberg
1

2. Geometrically-­‐locked
vortex
lattices
in
semiconductor
quantum
fluids
Supplementary
Information
0
8
a 1.540
d g
Energy (eV)
space (um)
4 1.539
0 10mW 10mW 1.538
-4 1.537 20
1.536
-8
8 1.540
b -20 -10 0 10 20 -4 e -2 0 2 4
Energy (eV)
space (um)
4 1.539 40
y
(μm)
time
(ps)
space (um) K vector (1/um)
0 18mW 18mW 1.538
1.537
-4
1.536 60
-8
8
c -20 -10 0 10 20
1.540
-4
f -2 0 2 4
Energy (eV)
space (um)
4 1.539
space (um) K vector (1/um)
0 1.538 80
22mW 30mW 1.537
-4
1.536 simulated
-8
-20 -10 0 10 20 -4 -2 0 2 4 100 -­‐10
-­‐5
0
5
10
K vector (1/um) x
(μm)
x
(μm)
space (um)
kx (μm )
-­‐1
Supplementary
Figure
S2|
Conditions
for
observing
stable
condensate
interference.
(a-­‐c)
Polariton
emission
images
for
two
pump
spots
placed
40𝜇𝑚
apart,
with
power
at
each
spot
indicated.
(d-­‐f)
Polariton
dispersions
corresponding
to
a
spatially-­‐apertured
20𝜇𝑚-­‐diameter
circle
centred
between
the
two
spots
in
(a-­‐c)
respectively.
It
is
clear
that
phase
locking
occurs
and
a
coherent
standing
wave
forms
only
when
outflowing
polaritons
from
each
spot
are
condensed
and
have
the
same
energy
(b,e).
On
the
other
hand,
if
pumping
bellow
threshold
(a,d)
or
with
asymmetric
powers
(c,e),
no
interferences
appear.
(g)
Simulated
time
evolution
along
the
central
line
connecting
two
pumping
spots,
one
at
−10𝜇𝑚
with
twice
the
intensity
of
the
other
at
10𝜇𝑚.
When
the
discrepancy
between
pumping
strengths
is
too
large,
the
relative
phase
between
the
two
independent
condensates
continuously
evolves,
shifting
the
fringes
in
time
(g),
thus
making
it
impossible
to
observe
in
a
time-­‐integrated
measurement
(c).
Because
of
the
nonlinear
potential
landscape
caused
by
the
feedback
between
polariton
density
and
local
blueshifts,
the
condition
subtly
varies
with
excitation
conditions.
G.
Tosi,
G.
Christmann,
N.G.
Berloff,
P.
Tsotsis,
T.
Gao,
Z.
Hatzopoulos,
P.G.
Savvidis,
J.J.
Baumberg
2

3. Geometrically-­‐locked
vortex
lattices
in
semiconductor
quantum
fluids
Supplementary
Information
a b c d
𝒌𝒐
20 µm
Supplementary
Figure
S3|
Hexagonal
lattice
wave-­‐function.
(a)
Measured
wavevector
distribution
corresponding
to
region
inside
the
dashed
green
circle
in
Fig.
1a.
Purple
triangles
show
lattice
momentum
at
the
spots
centroid,
𝑘! .
(b)
Estimated
spatially-­‐dependent
polariton
energy
blueshifts.
(c)
Spatially-­‐dependent
radial
wavevector
calculated
from
the
inverse
dispersion
relation,
Eq.
(1),
using
𝛥 𝒓
from
panel
(b).
(d)
Simulated
spatial
intensity
of
the
lattice
wave-­‐function,
𝜓 𝑟 ! ,
using
Eq.
S1
and
panels
(b,c).
Simulated
data
correspond
to
an
experimental
excitation
power
equal
to
20mW
at
each
spot.
Length
scale
in
(b-­‐d)
marked
in
(d).
G.
Tosi,
G.
Christmann,
N.G.
Berloff,
P.
Tsotsis,
T.
Gao,
Z.
Hatzopoulos,
P.G.
Savvidis,
J.J.
Baumberg
3

4. Geometrically-­‐locked
vortex
lattices
in
semiconductor
quantum
fluids
160 170 180 190 200 210 220 230 240
Supplementary
Information
160
20 30 40 50 60 70 80 90
170
a c e
180
80
190
90
200
100
210
110
160 170 180 190 200 210 220 230 240
180240 170230 160220
120
30 40 50 2 µm
60 70 80 90
80 130
b#! ! d f
190
90
" "
200
100
210
! !
110
#"
220
"
120
230
240
130
Supplementary
Figure
S4|
Ordered
square
lattices.
(a)
Intensity
and
(b)
phase
image
of
simulated
interference
between
four
perpendicular
plane
waves
with
π-­‐phase
relative
shifts.
No
vortex
is
observed;
instead,
square
intensity
lobes
of
constant
phase
appear
separated
by
dark-­‐soliton
stripes
with
π-­‐phase
shifts.
Such
a
pattern
is
not
observed
experimentally
due
to
instabilities
that
generate
vortices
at
random
positions
between
the
lobes.
(c)
Intensity
and
(d)
phase
image
of
simulated
interference
between
four
perpendicular
plane
waves,
one
of
them
having
a
π-­‐phase
shift.
Here
vortices
appear
regularly
placed
in
a
square
grid.
Such
a
pattern
is
also
observed
experimentaly
for
assymetric
pumps
(e,f).
G.
Tosi,
G.
Christmann,
N.G.
Berloff,
P.
Tsotsis,
T.
Gao,
Z.
Hatzopoulos,
P.G.
Savvidis,
J.J.
Baumberg
4

5. Geometrically-­‐locked
vortex
lattices
in
semiconductor
quantum
fluids
Supplementary
Information
x (µm) x (µm)
-2 -1 0 1 2 -2 -1 0 1 2
-2 a -2
b
Intensity
-1 1 2 -1 1 2
y (µm)
y (µm)
1
0 0
1 3 4 1 3 4
Simulations Experiments
2 2 0
c d e
π/2
Phase
Spot 1 Lobe 1 Lobe 1
0 Spot 2
Spot 3
Lobe 2
Lobe 3
Lobe 2
Lobe 3
Spot 4 Lobe 4 Lobe 4
-π/2
Simulations Simulations Experiments
0 4 8 12 0 4 8 12 0 4 8 12
Time (ps) Time (ps) Time (ps)
Supplementary
Figure
S5|
Non-­‐linear
square
lattice.
(a)
Simulated
and
(b)
measured
time-­‐averaged
polariton
emission
of
AF
lattice
corresponding
to
Fig.
3i
and
Fig.
3f,g,
respectively.
(c)
Time
evolution
of
the
simulated
wavefunction
phase
at
each
pump
spot
position.
(d)
Simulated
and
(e)
measured
time
evolution
of
the
relative
wavefunction
phase
at
each
lobe
indicated
in
(a,b).
G.
Tosi,
G.
Christmann,
N.G.
Berloff,
P.
Tsotsis,
T.
Gao,
Z.
Hatzopoulos,
P.G.
Savvidis,
J.J.
Baumberg
5

6. Geometrically-­‐locked
vortex
lattices
in
semiconductor
quantum
fluids
Supplementary
Information
-2 -1 0
0 x (µm)
Vorticity
-2 -1 0
0 -2 -1 0
Vorticity
-2 -1 0
-0.5 a
y (µm) (µm) (µm)
2 1 Time (ps)
Time (ps) 1
0 x (µm)
10
Vorticity
10
8
6
4
2
0
8
6
4
2
0
2 1 0
0.5 -2 -1 0
-2
-2
-2
Intensity
Time (ps)
4
y
2 -0.5 b
-2 -1 -1 1 0
Time (ps)
4 x (µm)
x (µm)
x
0
Vorticity
0.5 -2 -1 0
-1
(µm)
-1µm-1)
-1
-1
6
dφ/dy
(
Time (ps)
y
4
-0.5 c -2 -1 -1 0
6 2 V
dφ/dy(µm )
1
(µm-1)
0 DS
10 AV
Vorticity
8
6 0.5 DS
0
0
0
dφ/dy -10
0 10
10
-10
0
-1
8 4 dφ/dy Circulation
(µm-1) (µm-1)
Time (ps)
1
Vorticity
Vorticity
-1
Vorticity (µm ) -10 0 10 -1 dφ/dy dφ/dy
10 2 -1 1
-1
1
-10
-1
1
0
10
0
10
8
0
0
-2
10 -1 60 -10 0
Supplementary
Figure
S6|
Vortex-­‐dark
soliton
trains.
Measured
(a)
emission
intensity,
(b)
phase-­‐map
dφ/dy
(µm-1)
x (µm)
Time (ps)
and
(c)
circulation
and
10 4
phase-­‐derivative
corresponding
to
the
region
inside
dashed
blue
box
in
-2 -1 0 -10 -1
x (µm)
x (µm) 𝑡 = 0,
showing
dark-­‐solitons
(DS),
vortex
(V)
and
antivortex
(AV).
Supplementary
Fig.
S5b
for
time
slice
10
-1
-1
-2 8
-1 0
x (µm) 6
dφ/dy
(µm-1)
0
10 -10 10
-2
-2
8
-2 -1 0
0
2
4
6
8
10
Time (ps) 0
x (µm)
10 -10
-2 -1 0
x (µm)
G.
Tosi,
G.
Christmann,
N.G.
Berloff,
P.
Tsotsis,
T.
Gao,
Z.
Hatzopoulos,
P.G.
Savvidis,
J.J.
Baumberg
6

7. Geometrically-­‐locked
vortex
lattices
in
semiconductor
quantum
fluids
Supplementary
Information
Simulations Experiments
a x (µm)
b x (µm)
p(vortex), Γ(𝒓)
-2 -1 0 1 2 -2 -1 0 1 2
-2 -2
probability (%)
vortex
-1 -1
y (µm)
y (µm)
"
0 0
1 1 10%
1%
2 -2 -1 0 2 -2 -1 0
c d0
Circulation
0
Vorticity
2 2 1
Time (ps)
4
Time (ps)
4
-1
6 6
dφ/dy
(µm-1)
10
8 8
0
10 10 -10
-2 -1 0 -2 -1 0
x (µm)
x (µm)
Supplementary
Figure
S7|
Vortex
and
dark-­‐soliton
nonlinear
dynamics
in
square
‘waveguides’.
(a)
Simulated
and
(b)
measured
time-­‐averaged
circulation
strength,
Γ(𝒓) .
(c)
Simulated
and
(d)
measured
time
evolution
of
the
vorticity
and
phase-­‐gradient
of
the
region
inside
the
dashed
red
box
in
(a,b)
integrated
along
the
𝑦-­‐axis
(see
Supplementary
Fig.
S6).
G.
Tosi,
G.
Christmann,
N.G.
Berloff,
P.
Tsotsis,
T.
Gao,
Z.
Hatzopoulos,
P.G.
Savvidis,
J.J.
Baumberg
7

8. Geometrically-­‐locked
vortex
lattices
in
semiconductor
quantum
fluids
Supplementary
Information
Supplementary
Discussion
Lattice
wave-­‐function.
Under
low
pump
power,
when
non-­‐linearities
do
not
play
a
significant
role,
each
pump
spot
contributes
to
the
global
wave-­‐function
with
a
superposition
of
different
𝑘 -­‐states
at
different
radial
positions5:
!!"#$!
𝜓 𝑟, 𝑡 ≈ !!! 𝑒! ! !"! !!(𝒓) . 𝒓!𝒓 𝒏 !!!
𝑔! 𝒓 𝑒 !! 𝒓!𝒓 𝒏 !!
(S1)
𝒓!𝒓 𝒏 !"(!!)
𝑡 𝒓− 𝒓𝒏 = !
𝑑𝑟′
(S2)
!" !!
The
blueshift
𝛥(𝒓)
is
maximum
at
the
spot
positions
and
decays
parabolically
going
to
zero
after
10𝜇𝑚
(Supplementary
Fig.
S3b).
The
radial
𝐾
wavevector
is
given
by
the
inverse
lower
polariton
branch
dispersion
relation
(Fig.
2e,
Supplementary
Fig.
S3a)
and
depends
on
the
blueshift
(Supplementary
Fig.
S3b).
The
expanding
density
decays
exponentially
according
to
the
polariton
lifetime
𝜏!
and
the
local
velocity
from
Eq.
(S2).
The
term
𝑔! 𝒓
describes
local
amplification13.
Hexagonal
lattices
appear
in
this
model
in
the
wavefunction
central
region,
reproducing
well
the
measured
pattern
(Supplementary
Fig.
S3d).
The
individual
condensate
phases
𝜑! ,
merely
spatially
shift
the
lattice
for
the
3
spot
case.
For
all
the
measured
data,
the
relative
phases
between
the
three
condensates
are
close
to
zero
(F
offset
<
3°)
and
are
well
described
by
the
linear
superposition
of
plane
waves.
Nonlinearities
and
relative
phases
play
a
much
more
important
role
for
the
4
spot
excitations
and
higher
powers,
but
we
also
found
square
lattices
that
can
be
well
reproduced
by
linear
interferences
(Supplementary
Fig.
S4c-­‐f).
G.
Tosi,
G.
Christmann,
N.G.
Berloff,
P.
Tsotsis,
T.
Gao,
Z.
Hatzopoulos,
P.G.
Savvidis,
J.J.
Baumberg
8

9. Geometrically-­‐locked
vortex
lattices
in
semiconductor
quantum
fluids
Supplementary
Information
Non-­‐linear
vortex
dynamics
in
the
square
lattice.
To
better
understand
the
nonlinear
dynamics,
the
time-­‐evolution
of
the
lattice
wavefunction
is
tracked
in
simulations
and
experiments,
in
the
latter
case
after
back
Fourier
transforming
the
complete
energy-­‐resolved
tomography
in
density
and
phase.
Tomographic
reconstruction
is
taken
by
sequentially
translating
the
spatial
images
across
the
entrance
slit
of
the
spectrometer,
thus
recording
spectra
for
each
line
scan
of
the
image.
The
phase
of
each
energy
mode
is
then
retrieved
from
interferences
of
each
tomographically
reconstructed
spatial
mode,
and
so
the
condensate
wave-­‐function
is
fully
characterized
in
terms
of
energy,
density
and
phase.
A
simple
Fourier
transform
allows
the
condensate
phase
and
density
to
be
tracked
in
time:
𝜓 𝒓, 𝑡 =
𝜓 𝒓, 𝐸 𝑒 !"#/ℏ!!(!) ,
with
𝜑(𝐸)
being
their
relative
phase
.
This
relative
phase
is
constrained
by
the
!
direct
images
of
polariton
density.
We
checked
also
that
𝜑(𝐸)
does
not
substantially
change
the
reconstruction
of
the
dynamics.
The
2meV
spectral
bandwidth
leads
to
dynamical
observations
on
the
𝑝𝑠-­‐timescale.
Even
though
the
AF-­‐coupled
lattice
is
stable
(Supplementary
Fig.
S5a-­‐c),
the
regions
between
the
bright
spots
which
are
expected
to
contain
dark-­‐soliton
stripes
are
destabilised
by
the
strong
nonlinear
interactions.
Under
high
pump
powers
non-­‐linear
dynamics
is
observed,
although
AF-­‐phase-­‐coupling
between
spots
is
preserved
and
the
time-­‐averaged
wave-­‐function
of
the
central
region
shows
the
characteristic
four
lobes
with
𝜋
phase
relation
between
them.
Under
high
polariton
densities,
dark-­‐solitons
breaks
up
into
vortex-­‐antivortex
pairs,
which
are
connected
by
dark
solitons
(Supplementary
Fig.
S6).
The
probability
of
finding
a
vortex
at
a
specific
spatial
point
is
given
by
the
normalised
time-­‐averaged
circulation,
Γ(𝒓) = 𝛤(𝒓, 𝑡) 𝑑𝑡 /∆𝑡,
mapped
in
Supplementary
Fig.
S7a,b.
We
note
that
the
experimental
spatial
resolution
for
the
accuracy
of
locating
the
vorticity
centre
of
the
larger
topological
vortex
(∼ 0.7 𝜆/2𝑁𝐴)
is
almost
the
pixel
size
here.
To
easily
visualize
such
vortex-­‐dark
soliton
trains,
we
extract
from
the
phase-­‐map
(Supplementary
Fig.
S6b)
and
plot
in
compatible
images
the
circulation
and
the
phase-­‐derivative
(Supplementary
Fig.
S6c),
along
with
the
polariton
density
(Supplementary
Fig.
S6a).
Averaging
over
this
small
section
of
y
between
two
bright
lobes,
allows
the
dynamics
of
these
vortices
and
the
phase-­‐gradient
to
be
observed.
An
intricate
time
dynamics
results
(Supplementary
Fig.
S7c,d),
with
moving
vortices
(red)
and
anti-­‐
vortices
(blue)
linking
dark
solitons
of
oppositely
directed
phase-­‐gradient,
producing
phase
fluctuations
between
the
bright
lobes
of
the
lattice
(Supplementary
Fig.
S5d,e).
Despite
their
non-­‐linear
time-­‐
dynamics,
the
topological
defects
remain
constrained
in
the
gaps
between
the
density
lobes,
which
form
vortex
‘waveguides’
(e.g.
Supplementary
Fig.
S7b).
G.
Tosi,
G.
Christmann,
N.G.
Berloff,
P.
Tsotsis,
T.
Gao,
Z.
Hatzopoulos,
P.G.
Savvidis,
J.J.
Baumberg
9

10. Geometrically-­‐locked
vortex
lattices
in
semiconductor
quantum
fluids
Supplementary
Information
Influence
of
disorder
on
the
geometric
coupling.
The
effect
of
disorder
on
the
geometric
coupling
robustness
is
studied
by
adding
a
random
potential
to
equation
(2):
!" ℏ!
𝑖ℏ = − ∇! + 𝑈! 𝜓 !
+ 𝑉!"# 𝒓 + 𝑖𝑃 𝒓, 𝜓 − 𝑖𝜅 𝜓
(S3)
!" !!
The
external
potential
𝑉!"#
contains
disorder
and
is
modelled
by
a
random
distribution
of
Fourier
modes
of
varying
amplitude
and
broadband
spatial
frequencies.
The
numerical
solution
of
this
equation
for
three
equally
spaced
pump
spots
and
no
disorder
( 𝑉!"# = 0)
always
gives
a
wavefunction
with
the
same
phase
from
each
spot
position,
and
so
the
central
bright
hexagon
appears
at
the
spots
centroid,
𝑂 .
When
pumping
with
four
equally-­‐spaced
spots
and
no
disorder,
two
stable
solutions
appear
depending
on
the
initial
noise:
one
with
equal
phases
at
each
pump
spot,
leading
to
a
maximum
intensity
in
the
centre,
and
the
other
with
a
π
phase
difference
between
neighbouring
spots,
leading
to
a
minimum
intensity
in
the
centre.
We
have
checked
that
this
effect
is
not
due
to
the
square
geometry
of
the
computational
grid
by
moving
the
positions
of
the
pumping
spots
around
the
centre.
Strong
disorder
introduces
phase-­‐shifts
during
propagation
out
from
each
spot,
and
so
the
lattice
is
displaced
and
the
geometric
coupling
is
lost.
However,
for
the
low
disorder
values
of
our
sample13,
geometric
coupling
is
preserved.
G.
Tosi,
G.
Christmann,
N.G.
Berloff,
P.
Tsotsis,
T.
Gao,
Z.
Hatzopoulos,
P.G.
Savvidis,
J.J.
Baumberg
10