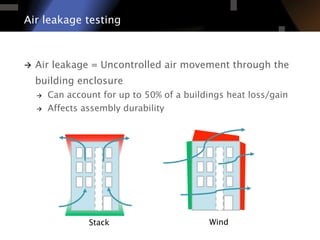
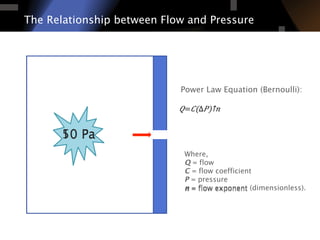
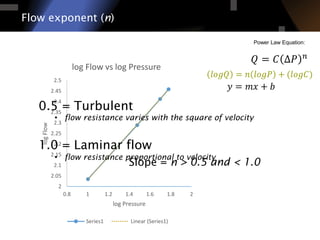
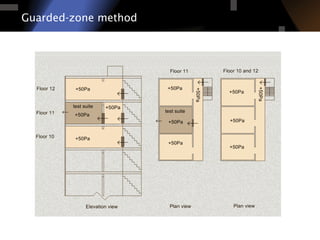
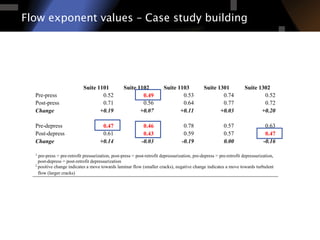
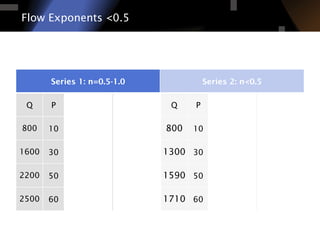
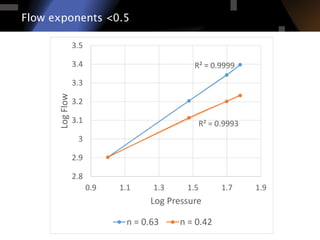
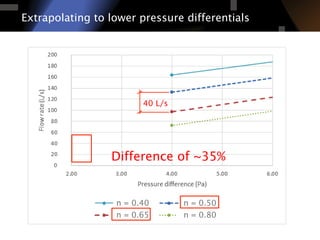
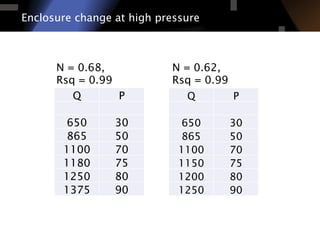
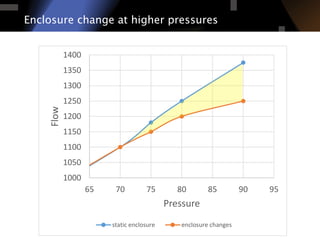
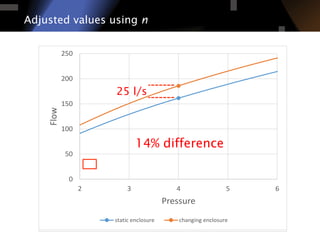
The document discusses air leakage testing and its impact on building energy efficiency, detailing the relationship between flow and pressure through flow exponent values. A case study is presented that showcases the effects of retrofitting on air leakage rates and the significance of flow exponent interpretations in evaluating building performance. It concludes that flow exponent values are critical for accurate energy modeling and compliance, while emphasizing the need for further research in this area.

1. Flow Exponent Values and
Implications for Air Leakage
Testing
NBEC 2014
ROBIN URQUHART, MBSC, MA NRES, RDH BUILDING ENGINEERING
DR. RUSSELL RICHMAN, P.ENG, RYERSON UNIVERSITY

2. Outline
à Introduction to air leakage testing
à Relationship between flow and pressure
à Case study building
à Abnormal flow exponents
à Data extrapolation to operating pressures
à Conclusions/Implications
à Further study

3. Air leakage testing
à Air leakage = Uncontrolled air movement through the
building enclosure
à Can account for up to 50% of a buildings heat loss/gain
à Affects assembly durability
Stack Wind

4. Fan induced pressure
à Induced pressure differentials using fans
à Mechanical
à Blower door
à ASTM E779-10 (10-60 Pa)
à multi-point
à ASTM 1827-12 (50 Pa)
à single point
à USACE (75 Pa)
à single point

5. Why test?
à Evaluate performance and determine retrofit options
à Single building
à Building stock
à Determine leakage rates for energy models
à 4 Pa – 10 Pa
à Code or other
specification compliance
à LEED, Energuide, etc.

6. The Relationship between Flow and Pressure
Pressure (P) and Flow (Q)
10 Pa50 Pa
Power Law Equation (Bernoulli):
𝑄= 𝐶​(∆ 𝑃)↑𝑛
Where,
Q = flow
C = flow coefficient
P = pressure
n = flow exponent (dimensionless).n = flow exponent

7. Flow exponent (n)
Power Law Equation:
2
2.05
2.1
2.15
2.2
2.25
2.3
2.35
2.4
2.45
2.5
0.8 1 1.2 1.4 1.6 1.8 2
log
Flow
log
Pressure
log
Flow
vs
log
Pressure
Series1 Linear
(Series1)
> 0.5 and < 1.0Slope = n
0.5 = Turbulent
• flow resistance varies with the square of velocity
1.0 = Laminar flow
• flow resistance proportional to velocity
𝑦 = 𝑚𝑥 + 𝑏

8. à 13-story MURB
à Enclosure retrofit 2012
à focus on air tightness
à Air leakage tested
à Pre-retrofit
à Post-retrofit
Case study building

9. Guarded-zone method

10. Flow exponent values – Case study buildingSuite 101 Suite 102 Suite 301 Suite 302 Suite 303
Pre-press 0.59 0.56 0.60 0.68 0.54
Post-press 0.56 0.67 0.75 0.85 0.85
Change2
-0.03 +0.11 +0.15 +0.17 +0.31
Pre-depress 0.92 0.80 0.50 0.62 0.61
Post-depress 0.79 0.69 0.60 0.57 0.37
Change -0.13 -0.11 +0.10 -0.05 -0.24
Suite 1101 Suite 1102 Suite 1103 Suite 1301 Suite 1302
Pre-press 0.52 0.49 0.53 0.74 0.52
Post-press 0.71 0.56 0.64 0.77 0.72
Change +0.19 +0.07 +0.11 +0.03 +0.20
Pre-depress 0.47 0.46 0.78 0.57 0.63
Post-depress 0.61 0.43 0.59 0.57 0.47
Change +0.14 -0.03 -0.19 0.00 -0.16
1 pre-press = pre-retrofit pressurization, post-press = post-retrofit depressurization, pre-depress = pre-retrofit depressurization,
post-depress = post-retrofit depressurization
2
positive change indicates a move towards laminar flow (smaller cracks), negative change indicates a move towards turbulent
flow (larger cracks)

11. “…blower door tests occasionally yield exponents less than the
Bernoulli limit of 0.5. In fact, it is physically impossible for such
low exponents to occur.”
Sherman, Wilson and Kiel. 1986
Flow exponents outside of theoretical range
So why do we get them?

12. Flow Exponents <0.5
Series 1: n=0.5-1.0 Series 2: n<0.5
Q P logQ logP n r-sq Q P logQ logP n r-sq
800 10 2.9
1
0.63 0.999 800 10 2.9
1
0.42 0.999
1600 30 3.2
1.48
1300 30 3.11
1.48
2200 50 3.34
1.7
1590 50 3.2
1.7
2500 60 3.4
1.78
1710 60 3.23
1.78

13. Flow exponents <0.5
R²
=
0.9999
R²
=
0.9993
2.8
2.9
3
3.1
3.2
3.3
3.4
3.5
0.9 1.1 1.3 1.5 1.7 1.9
Log
Flow
Log
Pressure
n
=
0.63 n
=
0.42

14. Geometry of the Enclosure
à Higher pressure differentials change
leakage path geometry
à Resulting in abnormal flow exponent
(n) values.
50 Pa10 Pa
à What effect on the data does a changing n
value cause?

15. Extrapolating to lower pressure differentials
40 L/s
Difference of ~35%
n = 0.40
n = 0.65
n = 0.50
n = 0.80

16. Q
P
650
30
865
50
1100
70
1180
75
1250
80
1375
90
Enclosure change at high pressure
Q
P
650
30
865
50
1100
70
1150
75
1200
80
1250
90
N = 0.68,
Rsq = 0.99
N = 0.62,
Rsq = 0.99

17. 600
700
800
900
1000
1100
1200
1300
1400
1500
20 40 60 80 100
Flow
Pressure
static
enclosure enclosure
changes
Enclosure change at higher pressures
1000
1050
1100
1150
1200
1250
1300
1350
1400
65 70 75 80 85 90 95
Flow
Pressure
static
enclosure enclosure
changes

18. 600
700
800
900
1000
1100
1200
1300
1400
1500
20 40 60 80 100
Flow
Pressure
static
enclosure enclosure
changes
Adjusted values using n
0
200
400
600
800
1000
1200
1400
0 20 40 60 80
Flow
Pressure
static
enclosure changing
enclosure
0
50
100
150
200
250
2 3 4 5 6
Flow
Pressure
static
enclosure changing
enclosure
25 l/s
14% difference

19. à The enclosure may not remain static throughout the
test
à The linear relationship may not be accurate at operating
pressure
à Substituting n values can have magnified impacts at
lower/higher pressure differentials
à R-squared values not perfect indicators
Conclusions

20. à Sizing mechanical systems
for predicted in operation
flow rates
à Retrofit options
Implications for the industry
à Energy models using extrapolated flow rates
may be inaccurate

21. à Multi-point testing still important
à Order of magnitude for comparison purposes
à Flow exponents tell us something, we might not know
exactly what it is
à Standards at higher pressures can be used for
compliance purposes
The Good

22. In-test corrections
à Check R-squared values during testing
à Check n values at the termination of each test
Post-test corrections
à Review data points and remove lowest pressure
differential point(s)
à If not reconciled, single point test at 50 Pa
Flow exponent corrections

23. à Sensitivity analysis: R-value threshold
à The use of flow exponent values in forensics
à Standardized leakage metric and pressure differential
for comparison purposes
à Effect on flow exponent of enclosure geometry
changes
Further study

24. Questions
ROBIN URQUHART
RURQUHART@RDH.COM