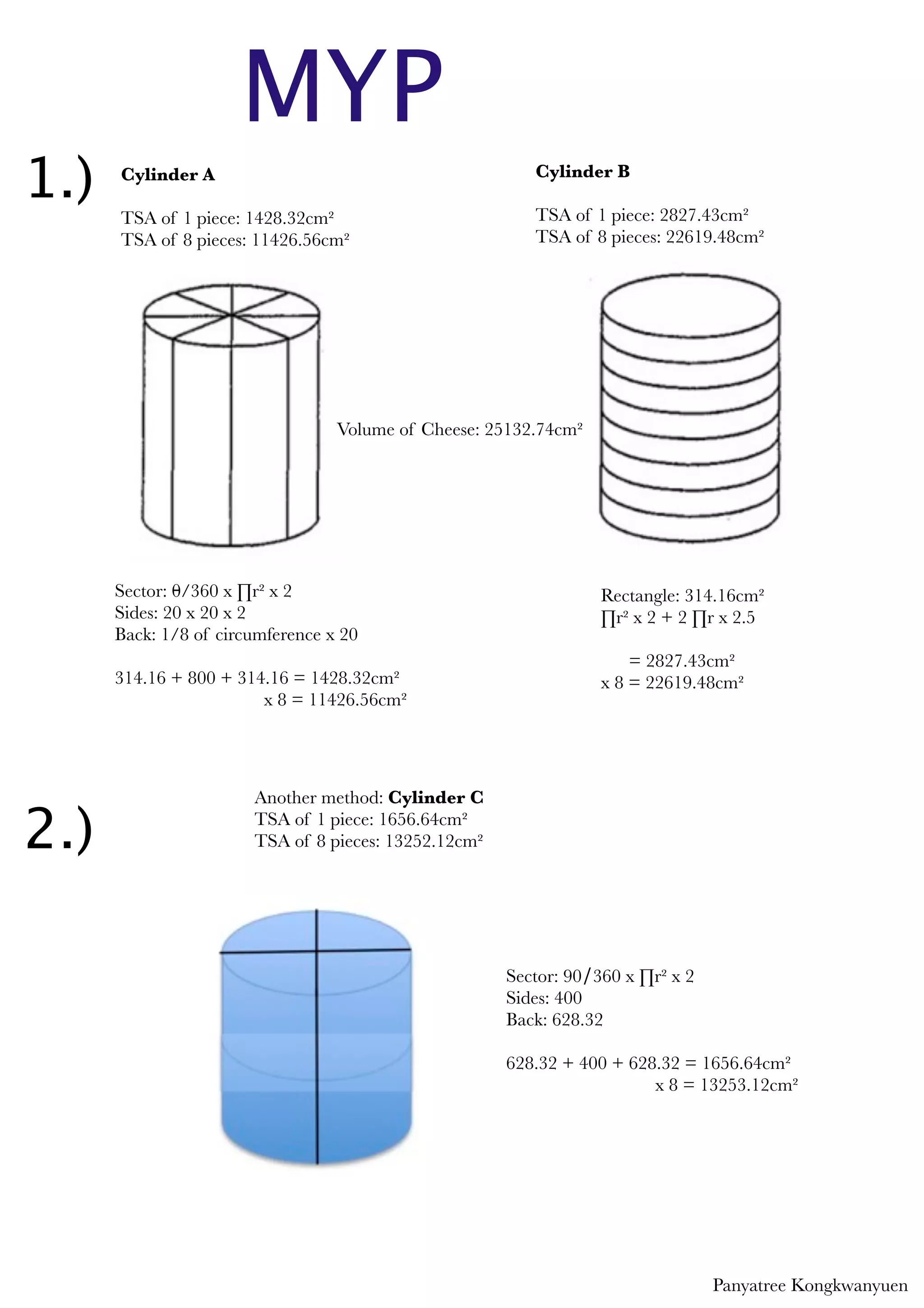
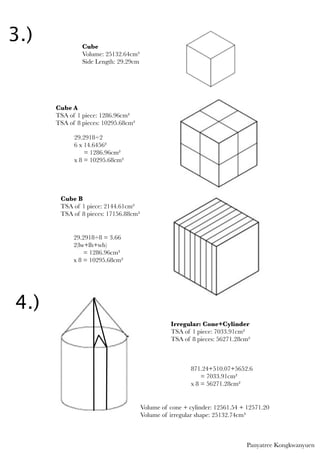
The document compares different methods of cutting a block of cheese into 8 equal pieces. It calculates the total surface area (TSA) of 1 piece and of all 8 pieces for different shapes, including cylinders, cubes, and an irregular shape. The table shows that cutting the cheese into cubes results in the lowest TSA of 10,295.68 cm2, making it the most efficient method. An irregular shape has the highest TSA of 56,271.28 cm2, making it the least efficient. Cutting the cheese into cubes is recommended as the simplest shape that minimizes surface area and potential for spoilage.

1. MYP
1.) Cylinder A
TSA of 1 piece: 1428.32cm²
Cylinder B
TSA of 1 piece: 2827.43cm²
TSA of 8 pieces: 11426.56cm² TSA of 8 pieces: 22619.48cm²
Volume of Cheese: 25132.74cm²
Sector: θ/360 x ∏r² x 2 Rectangle: 314.16cm²
Sides: 20 x 20 x 2 ∏r² x 2 + 2 ∏r x 2.5
Back: 1/8 of circumference x 20
= 2827.43cm²
314.16 + 800 + 314.16 = 1428.32cm² x 8 = 22619.48cm²
x 8 = 11426.56cm²
Another method: Cylinder C
2.) TSA of 1 piece: 1656.64cm²
TSA of 8 pieces: 13252.12cm²
Sector: 90∕360 x ∏r² x 2
Sides: 400
Back: 628.32
628.32 + 400 + 628.32 = 1656.64cm²
x 8 = 13253.12cm²
Panyatree Kongkwanyuen

2. 3.) Cube
Volume: 25132.64cm³
Side Length: 29.29cm
Cube A
TSA of 1 piece: 1286.96cm²
TSA of 8 pieces: 10295.68cm²
29.2918÷2
6 x 14.6456²
= 1286.96cm²
x 8 = 10295.68cm²
Cube B
TSA of 1 piece: 2144.61cm²
TSA of 8 pieces: 17156.88cm²
29.2918÷8 = 3.66
2(lw+lh+wh)
= 1286.96cm²
x 8 = 10295.68cm²
4.)
Irregular: Cone+Cylinder
TSA of 1 piece: 7033.91cm²
TSA of 8 pieces: 56271.28cm²
871.24+510.07+5652.6
= 7033.91cm²
x 8 = 56271.28cm²
Volume of cone + cylinder: 12561.54 + 12571.20
Volume of irregular shape: 25132.74cm³
Panyatree Kongkwanyuen

3. Table
Shape TSA of 1 piece (cm²) TSA of 8 pieces (cm²) Volume (cm³)
Cylinder A 1428.32 11426.56 25132.74
Cylinder B 2827.43 22619.48 25132.74
Cylinder C 1656.64 13252.12 25132.74
Cube A 1286.96 10295.68 25132.64
Cube B 2144.61 17156.88 25132.64
Irregular 7033.91 56271.28 25132.74
5 - 6.)
From the data show on the table, Cube A’s method of cutting the cheese is most efficient
because it has the least surface area (10295.68 cm²). Whereas when cutting the irregular shape, it has
the most total surface area. I would suggest the supermarket owner cut up his cheese in cubes because
it creates the least total surface area, another reason being it is normally more common. I think that
the more complex the shape of the cheese is, the more total surface area it will have, which will be
unfortunate on the store owner because the cheese will go stale faster. Especially with irregular shapes,
it is more difficult to cut the cheese into eight equal pieces. I don’t think the shop owner would want to
spend time calculating where to cut the cheese.
Another method that could work well is Cylinder A’s method, by cutting the cheese into
triangular prisms. There might be a huge difference in the total surface area for Cube A and Cylinder
A, but if the owner wants a variety of shapes, this method is the second best. However, judging shape
wise, customers should prefer cube, triangular, or cylinder shaped block of cheese.
I am not quite familiar with the numbers for total surface areas of objects so I am not sure if
these big numbers are reasonable. Although all the measurements are all around the same type of big
numbers so I assume that these numbers are reasonable. Though I think there is something weird
about my result for the irregular shape because it has a huge number compared to the other numbers
on the table. My results are show in second decimal places because measurements at the super market
are, on average, to the nearest 2 decimal places. For the cube section, there is a 0.1cm² difference from
the original volume of the cheese. This may affect the data. However, in the original volume, which
was calculated from the cylinder, Pi (∏) also affects the volume.
Panyatree Kongkwanyuen