This document describes an introduction to EECS140 Analog Circuit Design course at UC Berkeley. The course will focus on designing MOS analog integrated circuits using SPICE simulations. It will cover applications like RF amplification and filtering. The course structure and prerequisites are provided. MOS device models including large and small signal equations are discussed. SPICE parameters for the MOS models are also presented.


![EECS140 ANALOG CIRCUIT DESIGN LECTURES ON MOS DEVICE MODELS
ROBERT W. BRODERSEN LECTURE 2
MOS Large Signal Equations (Cont.)
VGS VT
<
VGS VT
>
VDS VD S A T
< VG S VT
–
=
Cutoff :
Linear :
IDS
k' W
L
-
-
-
-
- VGS
VT
–
VDS
2
-------
–
VDS
⋅
⋅ ⋅
=
Saturated :
VGS VT
>
VDS VD S A T
> VG S VT
–
=
IDS
k'
2
---
W
L
-
-
-
-
- VG S VT
–
( )2
1 λ VDS
⋅
+
( )
⋅ ⋅
=
M-4
EECS140 ANALOG CIRCUIT DESIGN LECTURES ON MOS DEVICE MODELS
ROBERT W. BRODERSEN LECTURE 2
MOS Large Signal Equations (Cont.)
VT VTo γ 2 φf
⋅ VS B
+
( )
1
2
-
-
-
2 φf
⋅
( )
1
2
-
-
-
–
[ ]
⋅
+
=
VTo Threshold Voltage @ VS B
≡ 0
=
VS B 0
>
( )
φf Fermi Potential 0.3
≈
≡
γ Body Effect Factor
≡
λ Short Channel Effect
≡
W Width of Device
≡
L Length
≡
k' µ Cox
⋅
=
Oxide Capacitance
mobility
E = VDS/L
E
µ
νε
M-5
EECS140 ANALOG CIRCUIT DESIGN LECTURES ON MOS DEVICE MODELS
ROBERT W. BRODERSEN LECTURE 2
MOS Large Signal Equations (Cont.)
VTo γ VS B
1
2
-
-
-
⋅
+
VT
VTo
VBS
0
γ
1
Co x
------ 2 q ε NA
⋅ ⋅ ⋅
⋅
=
n n
G
S D
Body Effect :
+ + + + + + + +
M-6
EECS140 ANALOG CIRCUIT DESIGN LECTURES ON MOS DEVICE MODELS
ROBERT W. BRODERSEN LECTURE 2
MOS Large Signal Equations (Cont.)
Short Channel Effect (λ):
Ldrawn
S G D
XJ = Junction Depth
LD = Lateral Diffusion ~ 0.75 XJ
XD
L Ldrawn 2 LD
⋅
–
=
LE F F L XD
–
=
XD f VDS
( )
=
M-7](https://image.slidesharecdn.com/moscharacteristics-230405202509-191fc885/85/MOS_Characteristics-3-320.jpg)

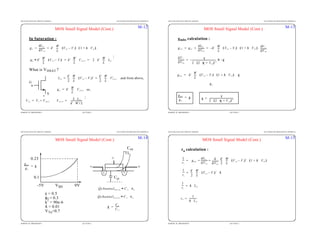
![EECS140 ANALOG CIRCUIT DESIGN LECTURES ON MOS DEVICE MODELS
ROBERT W. BRODERSEN LECTURE 3
MOS Small Signal Model (Cont.)
Model Parameters in Spice Level 1:
KP k' µ Co x nmos 50 100µ
A
V
2
-
-
-
-
-
–
→
∼
⋅
= =
LAMBDA λ 0.01 0.1
→
∼
=
PHI 2 φf 0.6
∼
⋅
=
VTO VTo 0.3 0.5Volts
→
∼
=
GAMMA γ 0.05 0.5
→
∼
=
pmos
1
3
-
-
-nmos
≈
M-16
EECS140 ANALOG CIRCUIT DESIGN LECTURES ON SPICE
ROBERT W. BRODERSEN LECTURE 4
MOS Small Signal Model (Cont.)
Summary:
gm 2 k'
W
L
-
-
-
-
- IDS
⋅ ⋅ ⋅
1
2
-
-
-
≈ k'
W
L
-
-
-
-
- VD S A T
⋅ ⋅
2 IDS
⋅
VDSAT
-------------
= =
gmbs χ g
⋅ m
=
χ
γ
2 2 φf VS B
+
⋅
( )0.5
⋅
-----------------------------------------
=
VD S A T
2 ID S
⋅
k' W L
⁄
⋅
--------------------
1
2
-
-
-
=
r0
1
λ IDS
⋅
-------------
=
IDS
gm
----- VG S VT
–
2
------------------ VDSAT
2
----------
= =
VD S A T VGS VT
–
=
VG S VT
2 IDS
⋅
k' W L
⁄
⋅
--------------------
1
2
-
-
-
+
=
IDS
k'
2
--- W
L
-
-
-
-
- VGS VT
–
( )2
⋅ ⋅
=
VT VT o γ 2 φf
⋅ VS B
+
( )
1
2
-
-
-
2 φf
⋅
( )
1
2
-
-
-
–
[ ]
⋅
+
=
EECS140 ANALOG CIRCUIT DESIGN LECTURES ON SPICE
ROBERT W. BRODERSEN LECTURE 4
University of California
Berkeley
College of Engineering
Department of Electrical Engineering
and Computer Science
Robert W. Brodersen
EECS140
Analog Circuit Design
Lectures
on
SPICE
EECS140 ANALOG CIRCUIT DESIGN LECTURES ON SPICE
ROBERT W. BRODERSEN LECTURE 4
SP-1
Spice Transistor Model :
M1 1 2 3 4 nch L=1µ W=10µ
AD=( ) AS=( ) PD=( ) PS=( ) NRD=( )
L
W
G
D
S
area of drain
parasitic resistors
1
2
3
4](https://image.slidesharecdn.com/moscharacteristics-230405202509-191fc885/85/MOS_Characteristics-6-320.jpg)


