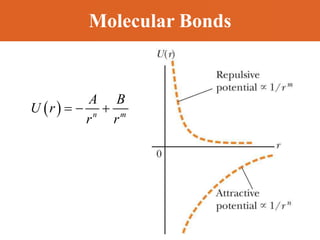
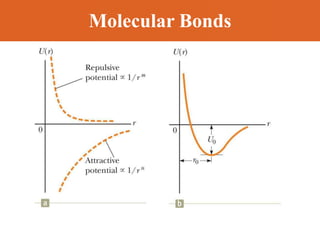
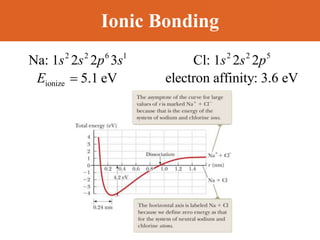
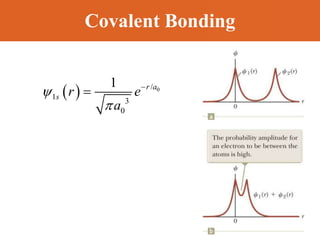
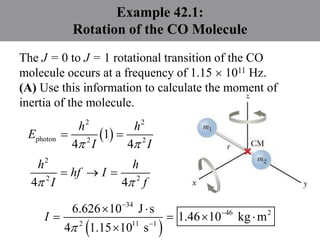
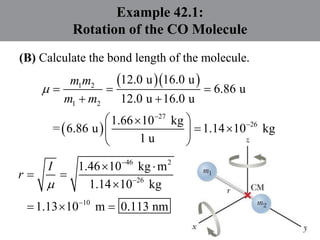
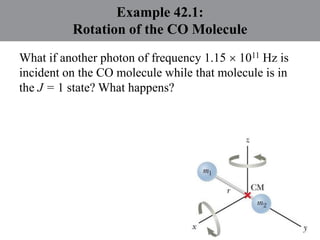
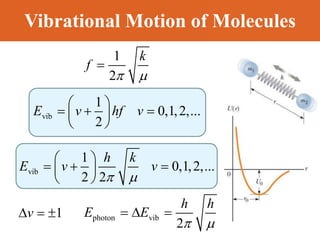
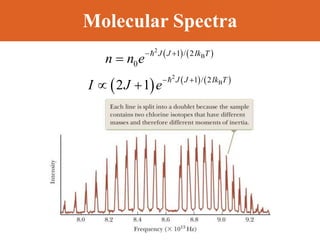
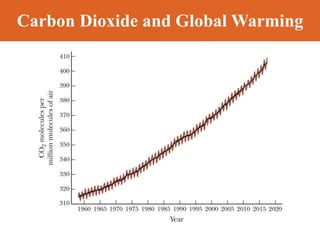
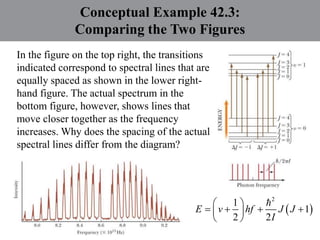
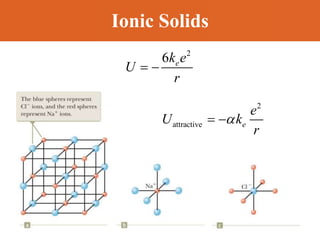
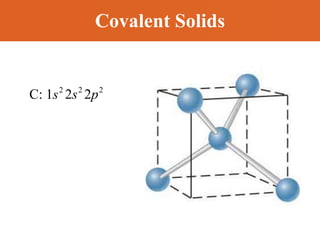
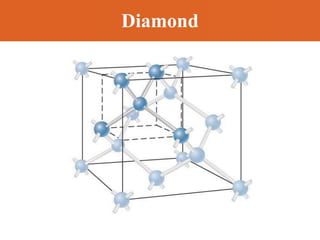
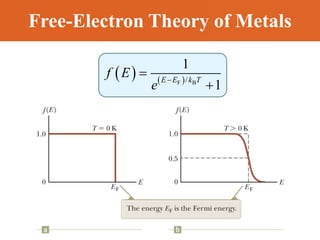
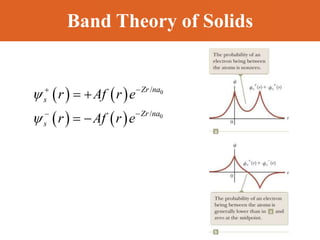
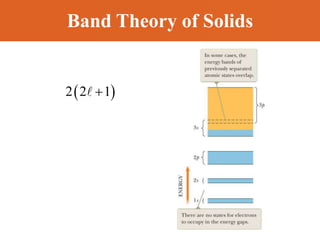
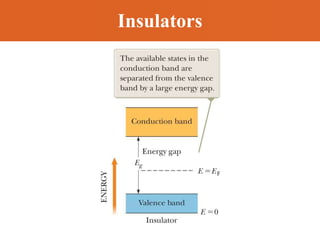
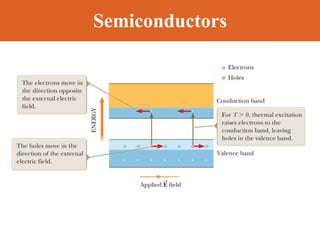
Chapter 42 discusses molecular bonds including ionic, covalent, and hydrogen bonding, with examples of each type provided. The chapter also covers molecular rotational and vibrational motions, including calculations related to energy transitions of molecules, along with quizzes for understanding. Additionally, it addresses the band theory of solids and materials classification, such as conductors, insulators, and semiconductors, with specific examples and calculations.

1. Chapter 42:
Molecules and Solids

2. Molecular Bonds
    
n m
A B
U r
r r

3. Molecular Bonds

4. Ionic Bonding
2 2 6 1
Na: 1 2 2 3
s s p s 2 2 5
Cl: 1 2 2
s s p
ionize 5.1 eV
E  electron affinity: 3.6 eV

5. Covalent Bonding
  0
/
1
3
0
1



 r a
s r e
a

6. Van der Waals Bonding

7. Hydrogen Bonding

8. Hydrogen Bonding

9. Quick Quiz 42.1
For each of the following atoms or molecules, identify
the most likely type of bonding that occurs between the
atoms or between the molecules. Choose from the
following list: ionic, covalent, van der Waals, hydrogen.
(a) atoms of krypton
(b) potassium and chlorine atoms
(c) hydrogen fluoride (HF) molecules
(d) chlorine and oxygen atoms in a hypochlorite ion
(ClO2)

10. Quick Quiz 42.1
For each of the following atoms or molecules, identify
the most likely type of bonding that occurs between the
atoms or between the molecules. Choose from the
following list: ionic, covalent, van der Waals, hydrogen.
(a) atoms of krypton: van der Waals
(b) potassium and chlorine atoms: ionic
(c) hydrogen fluoride (HF) molecules: hydrogen
(d) chlorine and oxygen atoms in a hypochlorite ion
(ClO2): covalent

11. Rotational Motion of Molecules
2
rot
1
2


E I 2
1 2
1 2
m m
I r r
m m

 
 
 

 
1 2
1 2
 

m m
m m
 
1
0,1,2,...
L J J
J
 

el trans rot vib
   
E E E E E
L I


12. Rotational Motion of Molecules
 
1 0,1,2,...
  
L J J J
 
 
 
 
2
2
2
2
rot
2
rot
1
1 1
2 2 2 2
1 0,1,2,...
2
J
J J
L
E I I
I I I
E E J J J
I
 

   
   

13. Rotational Motion of Molecules
   
2
photon rot 1
2 2
photon 2
1 1
2
1,2,3,...
4
J J
E E E E J J J J
I
h
E J J J
I I


       
 
 
  
1
J
   1 1,2,3,...
J J
E E J

 
photon
E hf

2
1 /4
f h I



14. Quick Quiz 42.2
A gas of identical diatomic molecules absorbs
electromagnetic radiation over a wide range of
frequencies. Molecule 1 is in the J = 0 rotation state and
makes a transition to the J = 1 state. Molecule 2 is in the J
= 2 state and makes a transition to the J = 3 state. The
ratio of the frequency of the photon that excited molecule
2 to that of the photon that excited molecule 1 is equal to
(a) 1
(b) 2
(c) 3
(d) 4
(e) impossible to determine?

15. Quick Quiz 42.2
A gas of identical diatomic molecules absorbs
electromagnetic radiation over a wide range of
frequencies. Molecule 1 is in the J = 0 rotation state and
makes a transition to the J = 1 state. Molecule 2 is in the J
= 2 state and makes a transition to the J = 3 state. The
ratio of the frequency of the photon that excited molecule
2 to that of the photon that excited molecule 1 is equal to
(a) 1
(b) 2
(c) 3
(d) 4
(e) impossible to determine?

16. Example 42.1:
Rotation of the CO Molecule
The J = 0 to J = 1 rotational transition of the CO
molecule occurs at a frequency of 1.15  1011 Hz.
(A) Use this information to calculate the moment of
inertia of the molecule.
 
2 2
photon 2 2
1
4 4
 
 
h h
E
I I
2
2 2
4 4
 
  
h h
hf I
I f
 
34
46 2
2 11 1
6.626 10 J s
1.46 10 kg m
4 1.15 10 s
I




 
   


17. Example 42.1:
Rotation of the CO Molecule
(B) Calculate the bond length of the molecule.
  
 
1 2
1 2
27
26
12.0 u 16.0 u
6.86 u
12.0 u 16.0 u
1.66 10 kg
= 6.86 u 1.14 10 kg
1 u
m m
m m



  
 
 

 
 
 
46 2
26
10
1.46 10 kg m
1.14 10 kg
1.13 10 m 0.113 nm




 
 

  
I
r

18. Example 42.1:
Rotation of the CO Molecule
What if another photon of frequency 1.15  1011 Hz is
incident on the CO molecule while that molecule is in
the J = 1 state? What happens?

19. Vibrational Motion of Molecules
1
2 

k
f
vib
1
0,1,2,...
2
 
  
 
 
E v hf v
vib
1
0,1,2,...
2 2 
 
  
 
 
h k
E v v
1
v
   photon vib
2 
  
h h
E E

20. Vibrational Motion of Molecules

21. Quick Quiz 42.3
A gas of identical diatomic molecules absorbs
electromagnetic radiation over a wide range of frequencies.
Molecule 1, initially in the v = 0 vibrational state, makes a
transition to the v = 1 state. Molecule 2, initially in the v =
2 state, makes a transition to the v = 3 state. What is the
ratio of the frequency of the photon that excited molecule 2
to that of the photon that excited molecule 1?
(a) 1
(b) 2
(c) 3
(d) 4
(e) impossible to determine

22. Quick Quiz 42.3
A gas of identical diatomic molecules absorbs
electromagnetic radiation over a wide range of frequencies.
Molecule 1, initially in the v = 0 vibrational state, makes a
transition to the v = 1 state. Molecule 2, initially in the v =
2 state, makes a transition to the v = 3 state. What is the
ratio of the frequency of the photon that excited molecule 2
to that of the photon that excited molecule 1?
(a) 1
(b) 2
(c) 3
(d) 4
(e) impossible to determine

23. Example 42.2:
Vibration of the CO Molecule
The frequency of the photon that
causes the v = 0 to v = 1 transition
in the CO molecule is 6.42  1013 Hz.
We ignore any changes in the rotational
energy for this example.
(A) Calculate the force constant k for this molecule.
2 2
4
2
 
 
  
h k
hf k f
  
2
2 26 13 1
3
4 1.14 10 kg 6.42 10 s
1.85 10 N/m
  
  
 
k

24. Example 42.2:
Vibration of the CO Molecule
(B) What is the classical amplitude
A of vibration for this molecule in
the v = 0 vibrational state?
1/4
2
1 1
2 4 2
   
 
    
 
h k h
kA A
k
  
1/4
34
26 3
12
6.626 10 J s 1
2 1.14 10 kg 1.85 10 N/m
4.79 10 m 0.00479 nm




 
 
 

 
 
 
  
A

25. Molecular Spectra
 
2
1
1
2 2
 
   
 
 
E v hf J J
I

26. Molecular Spectra
   
2
photon 1 0,1,2,... 1
E E hf J J J
I
        
 
2
photon
1,2,3,... 1
E E hf J
I
J J
   
   

27. Molecular Spectra
   
2
B
1 / 2
0
 
 J J Ik T
n n e
     
2
B
1 / 2
2 1  
  J J Ik T
I J e

28. Carbon Dioxide and Global Warming

29. Conceptual Example 42.3:
Comparing the Two Figures
In the figure on the top right, the transitions
indicated correspond to spectral lines that are
equally spaced as shown in the lower right-
hand figure. The actual spectrum in the
bottom figure, however, shows lines that
move closer together as the frequency
increases. Why does the spacing of the actual
spectral lines differ from the diagram?
 
2
1
1
2 2
 
   
 
 
E v hf J J
I

30. Ionic Solids
2
attractive 
  e
e
U k
r
2
6 e
k e
U
r
 

31. Covalent Solids
2 2 2
C: 1 2 2
s s p

32. Diamond

33. Graphite

34. Buckmisterfullerene

35. Graphene

36. Metallic Solids

37. Free-Electron Theory of Metals
   
F B
/
1
1



E E k T
f E
e

38. Free-Electron Theory of Metals
2 2 2
2 2
2 2
1,2,3,...
8 2

   
  
   
   
n
h
E n n n
mL mL
 
2 2
2 2 2
2
2

  
x y z
e
E n n n
m L
2 2
2
3
2 e
E
m L



39. Density of States
 
3/2
1/2
3
8 2
 e
m
g E dE E dE
h
     
N E dE g E f E dE

 
 
F B
3/2
1/2
3 /
8 2 1
1
e
E E k T
N E dE
m
E dE
h e


  
   
  
 
 

40. Fermi Energy
   
F B
3/2 1/2
3 /
0 0
8 2
1

 

 

 
e
e E E k T
m E dE
n N E dE
h e
F
3/2 3/2
1/2 3/2
F
3 3
0
8 2 8 2
2
for 0:
3
E
e e
e
m m
T n E dE E
h h
 
  

2/3
2
F
3
2 8
e
e
n
h
E
m 
 
  
 
avg F
3
5

E E

41. Example 42.4:
The Fermi Energy of Gold
Each atom of gold (Au) contributes one free electron to
the metal. Compute the Fermi energy for gold.
 
 
 
 
2/3
2
34 28 3
F 19
19
6.626 10 J s 3 5.90 10 m
0
8
2 9.11 10 J
8.85 10 J 5.53 eV
E

 


 
  
 

  
 
  

42. Band Theory of Solids
   
   
0
0
/
/
Zr na
s
Zr na
s
r Af r e
r Af r e






 
 

43. Band Theory of Solids
 
2 2 1


44. Metals

45. Insulators

46. Semiconductors

47. Semiconductors

48. Quick Quiz 42.4
Consider the data on three materials given in the table.
Identify each material as a conductor, and insulator, or a
semiconductor.
Material Conduction Band Eg
A Empty 1.2 eV
B Half full 1.2 eV
C Empty 8.0 eV

49. Quick Quiz 42.4
Consider the data on three materials given in the table.
Identify each material as a conductor, and insulator, or a
semiconductor.
A: semiconductor; B: conductor; C: insulator
Material Conduction Band Eg
A Empty 1.2 eV
B Half full 1.2 eV
C Empty 8.0 eV

50. Doped Semiconductors

51. Doped Semiconductors

52. Semiconductor Devices

53. The Junction Diode

54. Diodes
 
B
/
0 1
e V k T
I I e 
 

55. Light-Emitting and
Light-Absorbing Diodes

56. Photovoltaic Solar Cells

57. Example 42.6:
Where’s the Remote?
Estimate the band gap of the semiconductor in the
infrared LED of a typical television remote control.
1240 eV nm
1000 nm
1.2 eV
hc
E hf

 




58. The Transistor

59. Resonant Tunneling Transistors

60. The Integrated Circuit