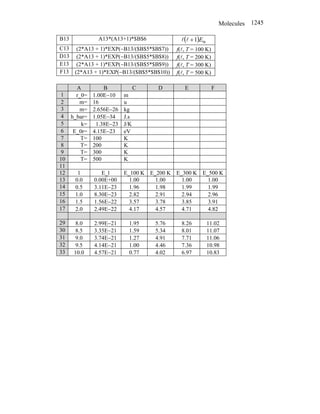
1. The document discusses concepts related to molecules, including:
- Polar vs non-polar molecules based on dipole moments
- Ionic vs covalent bonding mechanisms
- Quantum numbers related to molecular rotation and vibration
- Estimating properties like bond lengths using concepts like potential energy
2. It works through conceptual problems calculating properties like ionization energies, bond energies, quantum numbers, and percentages of ionic character in bonds.
3. The problems involve setting up and solving equations related to molecular structure, energies, and quantum mechanics.










![Molecules 1235
infinite separation. The net force acting on the ions is the sum of Frep and Fe. We can find
Frep from Urep and Fe from Coulomb’s law and then use dU/dr = Fnet = 0 at r = r0 to solve
for n.
Express the net force acting on the
ions:
e
rep
net F
F
F +
= (1)
Find Frep from Urep:
[ ]
1
1
rep
rep
+
−
−
−
−
=
−
=
=
=
n
n
n
r
nC
nCr
Cr
dr
d
dr
dU
F
The electrostatic potential energy of
the two ions as a function of
separation distance is given by:
r
ke
U
2
e −
=
Find the electrostatic force of
attraction Fe from Ue: 2
2
2
e
e
r
ke
r
ke
dr
d
dr
dU
F =
⎥
⎦
⎤
⎢
⎣
⎡
−
=
=
Substitute for Frep and Fe in equation
(1) to obtain: 2
2
1
net
r
ke
r
nC
F n
+
−
= +
Because dU/dr = Fnet = 0 at
r = r0: 2
0
2
1
0
0
r
ke
r
nC
n
+
−
= +
Multiply both sides of this equation
by r0 to obtain:
( ) ( )
0
e
0
rep
0
2
0
0 r
U
r
nU
r
ke
r
nC
n
+
−
=
+
−
=
Solve for n to obtain: ( )
( )
0
rep
0
e
r
U
r
U
n =
25 •••
Picture the Problem Urep at r = r0 is related to Ue, Ed, and ∆E through
( )
E
E
U
U ∆
+
+
−
= d
e
rep . The net force is the sum of Frep and Fe. We can find Frep from
Urep and Fe from Coulomb’s law. Because Fnet = 0 at r = r0, we can obtain simultaneous
equations in C and n that we can solve for each of these quantities.
(a) Urep is related to Ue, Ed, and ∆E
according to:
( )
E
E
U
U ∆
+
+
−
= d
e
rep
where ∆ENaCl = 1.52 eV](https://image.slidesharecdn.com/ismchapter37-220316050710/85/solucion-cap-37-11-320.jpg)
![Chapter 37
1236
Ue(r0) is given by:
0
2
e
r
ke
U −
=
where ke2
= 1.44 eV⋅nm
Substitute numerical values and
evaluate Ue:
eV
10
.
6
nm
236
.
0
nm
eV
44
.
1
e −
=
⋅
−
=
U
Substitute numerical values and
evaluate Urep:
( )
eV
31
.
0
eV
52
.
1
eV
27
.
4
eV
10
.
6
rep
=
+
+
−
−
=
U
(b) Express the net force acting on
the Na+
and Cl−
ions:
e
rep
net F
F
F +
= (1)
Find Frep from Urep:
[ ]
1
1
rep
rep
+
−
−
−
−
=
−
=
=
=
n
n
n
r
nC
nCr
Cr
dr
d
dr
dU
F
The electrostatic force of attraction
is: 2
2
e
r
ke
F =
Substitute for Frep and Fe in equation
(1) to obtain: 2
2
1
net
r
ke
r
nC
F n
+
−
= +
Because Fnet = 0 at r = r0:
2
0
2
1
0
0
r
ke
r
nC
n
+
−
= +
or
( ) ( )
0
rep
0
0
e r
nU
r
C
n
r
U n
=
=
Solve for n and C to obtain: ( )
( )
0
rep
0
e
r
U
r
U
n =
and
( ) n
r
r
U
C 0
0
rep
=
From (a): ( ) eV
10
.
6
0
e −
=
r
U
( ) eV
31
.
0
0
rep =
r
U
and, from Figure 37-1,](https://image.slidesharecdn.com/ismchapter37-220316050710/85/solucion-cap-37-12-320.jpg)














![Chapter 37
1252
Evaluate λ(H2):
( ) m
25
.
2
eV
550
.
0
nm
eV
1240
H2 µ
λ =
⋅
=
Evaluate λ(HD):
( ) m
60
.
2
eV
477
.
0
nm
eV
1240
HD µ
λ =
⋅
=
Evaluate λ(D2):
( ) m
19
.
3
eV
389
.
0
nm
eV
1240
D2 µ
λ =
⋅
=
43 ••
Picture the Problem We can set the derivative of the potential energy function equal to
zero to find the value of r for which it is either a maximum or a minimum. Examination
of the second derivative of this function at the value for r obtained from setting the first
derivative equal to zero will establish whether the function is a relative maximum or
relative minimum at this point.
Differentiate the potential energy
function with respect to r:
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
−
⎟
⎠
⎞
⎜
⎝
⎛
−
=
⎪
⎭
⎪
⎬
⎫
⎪
⎩
⎪
⎨
⎧
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
−
⎟
⎠
⎞
⎜
⎝
⎛
=
5
11
0
6
12
0
12
12
2
r
a
r
a
r
U
r
a
r
a
U
dr
d
dr
dU
Set the derivative equal to zero:
extrema
for
0
12
12
5
0
11
0
0
0
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
=
r
a
r
a
r
U
dr
dU
Solve for r0 to obtain, as our
candidate for r that minimizes the
Lenard-Jones potential:
a
r =
0
To show that r0 = a corresponds to a
minimum, differentiate U a second
time to obtain:
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
−
⎟
⎠
⎞
⎜
⎝
⎛
=
⎪
⎭
⎪
⎬
⎫
⎪
⎩
⎪
⎨
⎧
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
−
⎟
⎠
⎞
⎜
⎝
⎛
−
=
4
10
2
0
5
11
0
2
2
60
132
12
12
r
a
r
a
r
U
r
a
r
a
r
U
dr
d
dr
U
d
Evaluate this second derivative of
the potential at r0 = a:
[ ] 0
72
60
132 2
0
2
0
2
2
>
=
−
=
=
a
U
a
U
dr
U
d
a
r
Therefore, we can conclude that r0 = a](https://image.slidesharecdn.com/ismchapter37-220316050710/85/solucion-cap-37-28-320.jpg)







