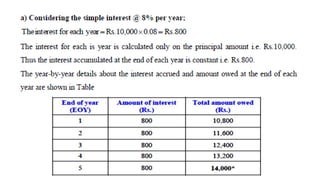
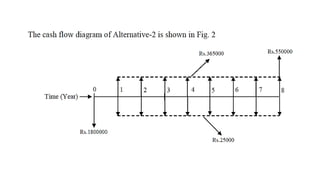
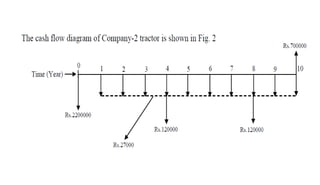
This document provides an overview of construction management, engineering economics, and related concepts. It defines construction management as overseeing project planning, design, and construction. Engineering economics involves evaluating design alternatives from an economic standpoint. Key terms are introduced, such as present worth, future worth, compound interest, cash flows, and factors used to analyze alternatives over time. Several examples of engineering economic calculations are provided.

1. CONSTRUCTION MANAGEMENT AND
ENGINEERING ECONOMICS
Module-1
Dr.Vinay Kumar B M

2. Syllabus

3. Construction Management
It is a professional service that uses
specialized, project management
techniques to oversee the planning,
design, and construction of a project,
from its beginning to its end.
Engineering Economics
It is the application of economic
techniques to the evaluation of design
and engineering alternatives.
The role of engineering economics is
to assess the appropriateness of a
given project, estimate its value, and
justify it from an engineering
standpoint.

4. Seven principles of Engineering Economics
1. Develop the alternatives
2. Focus on the differences
3. Use a consistent viewpoint
4. Use a common unit of measure
5. Consider all relevant criteria
6. Make uncertainty explicit
7. Revisit your decision

5. Basic Terminologies
Present Worth
Present worth, Present Value and Principal all represent the value of money at
time zero, which is the beginning of the engineering economic analysis period
under investigation.
In formulas, the present sum of money may be labeled as PW, PV, P or P0. All
four of these symbols represent the same initial time frame, which is time
zero.

6. Future Worth
• Future worth (FW), future value (F) or (F0) represent the future sum of
money including principal plus interest.
• Future values occur at any point in time in the future and they are usually
designated as the end of the engineering economic analysis period if they
are the last activity to occur in the analysis period.

7. Annuities: Uniform Series
• Annuities represent a payment or disbursement stream deposited or
withdrawn at equal set intervals such as daily, weekly, monthly, or yearly.
• As each annuity is deposited into an interest bearing account, it begins to
draw interest at the end of each compounding period.

8. Salvage value
• The salvage value is what an asset is worth at the end: of its useful life. In
engineering economic analysis, the salvage value is represented by a
future value occurring at the end of the analysis period.
• It is not always possible to accurately determine what a future salvage
value of an asset will be; therefore, for the purpose of an analysis, a
reasonable salvage value is assumed and included· in the calculations.

9. Sunk Cost
• Sunk cost is a difficult concept to understand when performing engineering
economic analysis.
• Sunk cost represents funds not recoverable because they have already
been expended sometime in the past. This is known as the past cost of an
equipment/asset.
• An example of a sunk cost would be spending $5 million on building a factory that is projected to cost $10 million. The $5 million already
spent—the sunk cost—should not be taken into account when deciding whether the factory should be completed

10. Marginal Cost
• Marginal cost of a product is the cost of producing an additional unit of that
product
• What is marginal cost example?
• Marginal cost refers to the additional cost to produce each additional unit. For example, it may cost $10 to make 10 cups of Coffee. To make another
would cost $0.80. Therefore, that is the marginal cost – the additional cost to produce one extra unit of output.
Marginal Revenue
• Marginal revenue of a product is the incremental revenue of selling an additional
unit of that product.

11. Opportunity Cost
• In practice, if an alternative (A) is selected from a set of competing alternatives
(A,B), then the corresponding investment in the selected alternative is not
available for any other purpose.
• If the same money is invested in some other alternative (B), it may fetch some
return. Since the money is invested in the selected alternative (A), one has to
forego the return from the other alternative (B).
• The amount that is foregone by not investing in the other alternative (B) is
known as the opportunity cost of the selected alternative (A).

12. Capitalized cost
• Capitalized cost is a term used in engineering economics and it refers to the
present worth of a project with an infinite life.
• In other words, capitalized cost is a lump sum of money needed today (t = 0)
to support an infinite life project simply on earned interest only.
• The concept of capitalized cost usually applies to public projects such as
airports, bridges, dams, and long term private projects such as hospitals and
private airports

13. Time value of money

14. • The time value of money (TVM) is the idea that money available at the
present time is worth more than the same amount in the future due to its
potential earning capacity.
• This core principle of finance holds that, money can earn interest, any
amount of money is worth more the sooner it is received.
• Time Value of Money (TVM) is an important concept in financial
management.

15. • It can be used to compare investment alternatives and to solve problems
involving loans, leases, savings.
• If a person invests his money today in bank savings, by next year he will
definitely accumulate more money than his investment. This accumulation
of money over a specified time period is called as time value of money.
• Similarly if a person borrows some money today, by tomorrow he has to pay
more money than the original loan. This is also explained by time value of
money.

16. • The time value of money is generally expressed by interest amount.
• The original investment or the borrowed amount (i.e. loan) is known as
the principal.
• The amount of interest indicates the increase between principal amount
invested or borrowed and the final amount received or owed.

17. • In case of an investment made in the past, the total amount of
interest accumulated till now is given by;
• Similarly in case of a loan taken in past, the total amount of interest is
given by;
In both the cases there is a net increase over the amount of money that
was originally invested or borrowed.

18. • When the interest amount is expressed as the percentage of the
original amount per unit time, the resulting parameter is known as
the rate of interest and is generally designated as “ i “.
• The time period over which the interest rate is expressed is known
as the interest period.
• The interest rate is generally expressed per unit year. However in
some cases the interest rate may also be expressed per unit month.

19. Example

21. Simple interest
• The interest is said to simple, when the interest is charged only on
the principal amount for the interest period.
• No interest is charged on the interest amount accrued during the
preceding interest periods.
• In case of simple interest, the total amount of interest accumulated
for a given interest period is simply a product of the principal
amount, the rate of interest and the number of interest periods.

22. • It is given by the following expression.
Simple interest reflects the effect of time value of money
only on the principal amount

23. Compound interest
• The interest is said to be compound, when the interest for any
interest period is charged on principal amount plus the interest
amount accrued in all the previous interest periods.
• Compound interest takes into account the effect of time value of
money on both principal as well as on the accrued interest also.

24. Example

28. Cash flow diagram
• The graphical representation of the cash flows i.e. both cash
outflows and cash inflows with respect to a time scale is generally
referred as cash flow diagram.

29. • The cash outflows (i.e. costs or expense) are generally represented by
vertically downward arrows whereas the cash inflows (i.e. revenue or
income) are represented by vertically upward arrows.
• In the cash flow diagram, number of interest periods is shown on the
time scale.
• The interest period may be a quarter, a month or a year.

30. • Since the cash flows generally occur at different time intervals within
an interest period, for ease of calculation, all the cash flows are
assumed to occur at the end of an interest period.
• In Fig. the cash outflows are Rs.100000, Rs.15000 and Rs.25000
occurring at end of year (EOY) “0” i.e. at the beginning, EOY “4” and
EOY “7” respectively.
• Similarly the cash inflows Rs.35000, Rs.80000 and Rs.45000 are
occurring at EOY “3”, EOY “6” and EOY “10” respectively.

31. Compound interest factors
• The compound interest factors and the corresponding formulas are
used to find out the unknown amounts at a given interest rate
continued for certain interest periods from the known values of
varying cash flows.
• The following are the notations used for deriving the compound
interest factors.

32. Unless otherwise stated, the rate of interest is compound interest
and is for the entire number of interest periods i.e. for “n” interest
periods.

33. • The present worth (P), future worth (F) and uniform annual worth (A)
are shown in Fig.

34. • In this figure the present worth, P is at the beginning and the uniform
annual series with annual value “A” is from end of year 1 till end of year
5.
• Both “P” and “A” are cash outflows.
• It may be noted that the uniform annual series with annual value “A”
may be also continued throughout the entire interest periods i.e. from
beginning till end of year 10 or for some intermediate interest periods
like commencing from end of year 3 till end of year 8.

35. • The future worth “F” is occurring at end of year 4 (cash outflow), at
end of year 6 (cash inflow) and at the end of year 10 (cash inflow).

36. Single payment compound amount factor (SPCAF)
• The single payment compound amount factor is used to compute the
future worth (F) accumulated after “n” years from the known
present worth (P) at a given interest rate ‘i’ per interest period.
• It is assumed that the interest period is in years and the interest is
compounded once per interest period.

37. The known present worth (P), unknown future worth (F) and the total
interest period “n” years are shown in Fig.

38. • The generalized formula for the future worth at the end of “n”
years is given by:
• The factor in equation is known as the single payment
compound amount factor (SPCAF).

39. Single payment present worth factor (SPPWF)
• The single payment present worth factor is used to determine the
present worth of a known future worth (F) at the end of “n” years
at a given interest rate ‘i’ per interest period.
• The present worth (P), future worth (F) and the total interest
period “n” years are shown in Fig.

40. • From the previous equation, the expression for the present worth
(P) can be written as follows;
• The factor in equation is known as single payment present
worth factor (SPPWF).

41. Uniform series present worth factor (USPWF)
• The uniform-series present worth factor is used to determine the
present worth of a known uniform series.
• Let “A” be the uniform annual amount at the end of each year,
beginning from end of year “1” till end of year “n”.
• The known “A”, unknown “P”, and the total interest period “n” years
are shown in Fig.

42. • This cash flow diagram refers to the case; if a person wants to get the
known uniform amount of return every year, how much he has to invest
now.
• The present worth (P) of the uniform series can be calculated by
considering each “A” of the uniform series as the future worth.

43. • Then the present worth (P) is calculated from the following equation:
• The factor within the bracket in equation is known as uniform series
present worth factor (USPWF).
• Thus if the value of “A” in the uniform series is known, then the
present worth P at interest rate of “i“ (per year) can be calculated by
multiplying the uniform annual amount “A” with uniform series
compound amount factor.

44. Capital recovery factor (CRF)
• The capital recovery factor is generally used to find out the
uniform annual amount “A” of a uniform series from the known
present worth at a given interest rate ‘i’ per interest period.
• The cash flow diagram is shown in Fig.

45. • This cash flow diagram indicates, if a person invests a certain amount
now, how much he will get as return by an equal amount each year.
• The expression for the uniform annual amount (A) can be written as
follows;
• The factor within bracket in equation is known as the capital recovery
factor (CRF).

46. Uniform series compound amount factor
• The uniform series compound amount factor is used to determine the
future sum (F) of a known uniform annual series with uniform amount
“A”.
• The cash flow diagram is shown in Fig.

47. • This cash flow diagram states that, if a person invests a uniform
amount at the end of each year continued for “n” years at interest rate
of “i” per year, how much he will get at the end of “n” years.
• This can be calculated from the following equation:
• The factor within bracket in equation is known as uniform series
compound amount factor (USCAF).

48. Sinking fund factor
• The sinking fund factor is used to calculate the annual amount “A‟ of a
uniform series from the known future sum “F”.
• The cash flow diagram is shown in Fig.

49. • This cash flow diagram indicates that, if a person wants to get a known
future sum at the end of “n” years at interest rate of “i” per year, how
much he has to invest every year by an equal amount.
• The expression for the uniform annual amount (A) can be written as
follows;
• The factor within bracket in equation is known as sinking fund factor
(SFF).

50. Interest factors with rate of interest ‘i’ (%) and number of
interest periods ‘n’

51. Problems
1. A person is investing 7,500/- every year in a recurring deposit of 8
years. What is the amount you can expect to receive if the
interest rate is 10%.
Ans: 85770/-

52. 2. What amount a person should invest every year in order to get lumsum
of 1 lakh at the end of 5 years. If the interest rate is 12%.
Ans : 15740/-
3.If a person borrows Rs.2,50,000/- now what is the uniform amount he is
expected to pay every year for next 7 years in order to repay the capital
amount borrowed? i = 10%
Ans : 51,160/-

53. 4. A person secures a loan of Rs.2,00,000 at a interest of 10%
compounded annually and starts an industry. The bank allows an free
period of 3 years. Calculate uniform end of payment to liquidate the debt
for a period of 9 years. What will be the total amount paid to the bank

55. 5. A person borrows Rs 1 lakh from a bank to start a enterprise. For first
four years he doesn’t repay the loan. But at the end of 4 years he
obtains a further loan of Rs.1 lakh from the bank. After 6 years he
starts repayment of both loans and clears them in a further period of 10
years. Calculate the yearly installment that he has to pay uniformly at 8%
interest rate.

57. 6. A Person takes a loan of 5 lakhs to start a industry at a rate of 15%. He
starts liquidating for 3 years after borrowing and opts for uniform period
of 16 years. Find out amount of each payment : (a) Yearly (b) Monthly.

59. Nominal and Effective Interest
• An interest rate takes two forms: nominal interest rate and effective
interest rate.
• The nominal interest rate does not take into account the compounding
period.
• The effective interest rate does take the compounding period into
account and thus is a more accurate measure of interest charges.

60. • A statement that the "interest rate is 10%" means that interest is 10%
per year, compounded annually.
• In this case, the nominal annual interest rate is 10%, and the effective
annual interest rate is also 10%.
• However, if compounding is more frequent than once per year, then the
effective interest rate will be greater than 10%.
• The more often compounding occurs, the higher the effective interest
rate.

61. • The relationship between nominal annual and effective annual interest
rates is:

62. Comparison of Alternatives

63. • For most of the engineering projects, equipments etc., there are
more than one feasible alternative.
• It is the duty of the project management team (comprising of
engineers, designers, project managers etc.) of the client
organization to select the best alternative that involves less cost and
results more revenue.
• For this purpose, the economic comparison of the alternatives is
made.

64. • The different cost elements and other parameters to be considered
while making the economic comparison of the alternatives are initial
cost, annual operating and maintenance cost, annual income or receipts,
expected salvage value, income tax benefit and the useful life.
• When only one, among the feasible alternatives is selected, the
alternatives are said to be mutually exclusive.

65. • In the economic comparison of alternatives, cost or expenses are
considered as negative cash flows, whereas the income or revenues are
considered as positive cash flows.
• From the view point of expenditure incurred and revenue generated, some
projects involve initial capital investment i.e. cash outflow at the beginning
and show increased income or revenue i.e. cash inflow in the subsequent
years.
• The alternatives having this type of cash flow are known as investment
alternatives.

66. Example: Purchase of a dozer by a construction firm.
• The construction firm will have different feasible alternatives for the
dozer with each alternative having its own initial investment, annual
operating and maintenance cost, annual income depending upon the
production capacity, useful life, salvage values etc.
• Hence the differences in different parameters namely initial capital
investment, annual operation cost, annually generated revenue,
expected salvage value, useful life, magnitude of output and its quality,
performance and operational characteristics etc. may exist among the
mutually exclusive alternatives.

67. Methods of Comparison of alternatives
1. Present worth method
2. Future worth method
3. Annual worth method
In these methods all the cash flows i.e. cash outflows and cash inflows
are converted into equivalent present worth, future worth or annual
worth considering the time value of money at a given interest rate per
interest period.

68. Comparison of alternatives by present worth
method
• In the present worth method for comparison of mutually exclusive
alternatives, the future amounts i.e. expenditures and incomes
occurring at future periods of time are converted into equivalent
present worth values at a certain rate of interest per interest
period and are added to present worth occurring at “0” time.
• The converted equivalent present worth values are always less than
the respective future amounts since the rate of interest is normally
greater than zero.

69. • Thus the cash flow of the mutually exclusive alternatives may consist of
future expenditures and incomes in different forms namely randomly
placed single amounts, uniform amount series commencing from end of
year 1, randomly placed uniform amount series i.e. commencing at time
period other than end of year 1.

70. • The methodology for the comparison of mutually exclusive
alternatives by the present worth method depends upon the
magnitude of useful lives of the alternatives.
• There are two cases;
a) The useful lives of alternatives are equal
b) The useful lives of alternatives are not equal.
The alternatives having equal useful lives are designated as
equal life span alternatives whereas the alternatives having
unequal life spans are referred as different life span

71. Equal life span alternatives
• The comparison of mutually exclusive alternatives having equal life
spans by present worth method is comparatively simpler than those
having different life spans.
• In case of equal life span mutually exclusive alternatives, the future
amounts as already stated are converted into the equivalent present
worth values and are added to the present worth occurring at time
zero

72. • Then the alternative that exhibits maximum positive equivalent
present worth or minimum negative equivalent present worth is
selected from the considered feasible alternatives.

73. Different life span alternatives
• In case of mutually exclusive alternatives, those have different life
spans, the comparison is generally made over the same number of
years i.e. a common study period.
• This is because; the comparison of the mutually exclusive
alternatives over same period of time is required for unbiased
economic evaluation of the alternatives.

74. • If the comparison of the alternatives is not made over the same life
span, then the cost alternative having shorter life span will result in
lower equivalent present worth i.e. lower cost than the cost
alternative having longer life span.

75. The two approaches used for economic comparison of different life span
alternatives are as follows:
1. Comparison of mutually exclusive alternatives over a time period that
is equal to least common multiple (LCM) of the individual life spans.
2. Comparison of mutually exclusive alternatives over a study period
which is not necessarily equal to the life span of any of the
alternatives.

76. Example -1

83. Example -2

90. Example - 3

97. Comparison of alternatives by future worth method
• In the future worth method for comparison of mutually exclusive
alternatives, the equivalent future worth (i.e. value at the end of the
useful lives of alternatives) of all the expenditures and incomes
occurring at different periods of time are determined at the given
interest rate per interest period.
• The equivalent future worth of these expenditures and incomes will
be determined using different compound interest factors namely
single payment compound amount factor and uniform series compound
amount factor

98. Example -4 (Using data of Example-1)

101. Example -7

107. Example - 8

112. Comparison of alternatives by annual worth
method
• In this method, the mutually exclusive alternatives are compared on
the basis of equivalent uniform annual worth.
• The equivalent uniform annual worth represents the annual equivalent
value of all the cash inflows and cash outflows of the alternatives at
the given rate of interest per interest period.
• In this method of comparison, the equivalent uniform annual worth of
all expenditures and incomes of the alternatives are determined
using different compound interest factors

113. • Since equivalent uniform annual worth of the alternatives over the
useful life are determined, same procedure is followed irrespective of
the life spans of the alternatives i.e. whether it is the comparison of
equal life span alternatives or that of different life span alternatives.
• In other words, in case of comparison of different life span
alternatives by annual worth method, the comparison is not made over
the least common multiple of the life spans as is done in case of
present worth and future worth method.

114. • The reason is that even if the comparison is made over the least
common multiple of years, the equivalent uniform annual worth of the
alternative for more than one cycle of cash flow will be exactly same
as that of the first cycle provided the cash flow i.e. the costs and
incomes of the alternative in the successive cycles is exactly same as
that in the first cycle.
• Thus the comparison is made only for one cycle of cash flow of the
alternatives

115. Example-9

120. Example -10