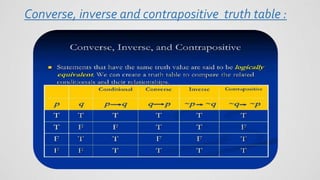
This document provides information about logical connectives and conditional statements. It defines conjunction, disjunction, implication, biconditional, converse, contrapositive, and inverse. Formulas are given for determining the truth values of statements connected by these logical operators based on the truth values of the individual propositions. Examples are given to illustrate conjunction, disjunction, and implication. The contrapositive, converse, and inverse are also defined. Finally, a truth table is referenced for evaluating the converse, inverse, and contrapositive of conditional statements.

1. Project 1
Discrete
mathematics
Considering the veracity of the statements p and q To determine the
truth values for a conjunction, disjunction, implication, bimplication,
converse, contrapositive, and inverse, use the following formula.
Name-> Dibyaman sahoo
Reg. no.->220301120212
Branch->B-tech (cse) 1st yr
Sec.->D

2. Conjunction
Disjunction
CONTENTS
BiImplication
Converse
Contrapositive and Inverse

3. Conjunction:
If p and q are two simple assertions, then "p q" proves their
combination. If propositions p and q are both true, the
conjunction has the value of true; otherwise, it has the value
of false.
EX-P: Ram is a boy
q:Ram has a car.
Ans: p ∧ q: Ram is a
boy and he has a car.

4. DISJUNCTION :
The disjunction is given by the value f if both p and q are false. The two
simple presentations p and q, denoted by "p q," form the compound
proposition "p or q."
EX-P: Ram is a boy
q:Ram has a car.
p∨q: Ram is a boy or
he has car.

5. EX- P: you work hard.
q:you will pass in the exam.
p → q: if you work hard then you will pass
in the examination
IMPLICATION :
If p and q are two simple statements, then the statement "if p than q,"
denoted by "p q," is the condition statement of p and q. The conditional
statement takes the value F if p is T and q is F. True unless it is false.

6. Biconditional :
The characters p and q stand for the biconditional statement with two
propositions. It is common to say that one conditional is true if and only if the
other is also true by using the phrase "if and only if" or the abbreviation "IFF."

7. CONTRAPOSITIVE:A contrapositive statement is created when the hypothesis and conclusion of a
statement are switched, and both are then refuted. If the hypothesis and conclusion are inverted in
this situation and both are rejected, the result is: If it's not a triangle, it's not a polygon. The
contrapositive of the statement "If a number n is even, then n2 is even" is "If n2 is not even, then n is
not even."
CONVERSE:The opposite statement can be obtained by swapping the values of "p" and "qlocations" in
the condition. If p = q, then q = p since p = q.
NVERSE:In an inverted statement, it is assumed that each of the original statements is untrue. The
complete reverse of "If it is snowing" would be "If it is not snowing." The complete reverse of
"then it is cold" would be "then it is not cold."

8. Converse, inverse and contrapositive truth table :

9. T H A N K
Y O U