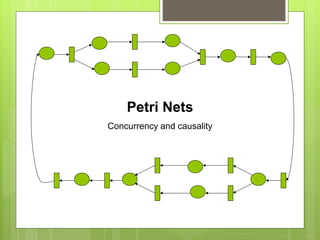
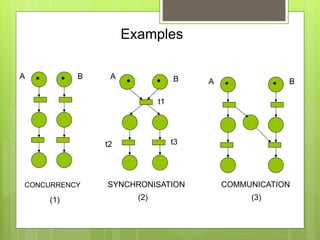
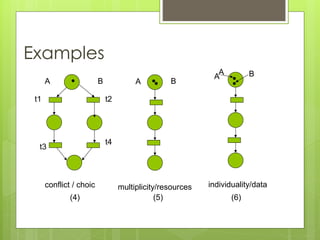
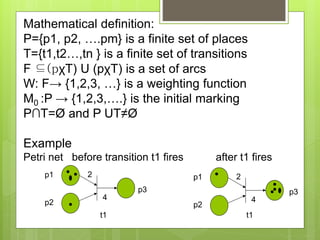
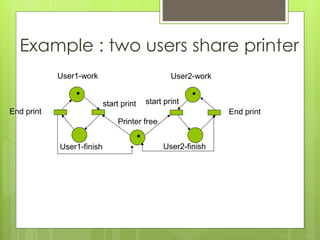
This document discusses modeling and simulation. It defines key terms like system, model, modeling, and simulation. It explains that modeling plays an important role in research and different fields by helping to understand, analyze, design, and control systems without having to physically build them. It discusses different types of models like physical, mental, flow charts, diagrams, and dynamic/static system models. It provides examples of modeling in fields like engineering and computer science. It outlines the steps to build a model, which includes clearly defining the problem, selecting relevant variables, and using logic and experience. The document also discusses the purposes of simulation like understanding behavior, testing, and discovering mistakes. Finally, it introduces Petri nets as a way to model concurrent

1. Modeling and
Simulation
‫المحاكاة‬ ‫و‬ ‫النمذجة‬
‫د‬
.
‫العلي‬ ‫خولة‬

2. ‫النظم‬
‫النظام‬ ‫مفهوم‬
‫النظام‬ ‫مهام‬ ‫ألداء‬ ً‫ا‬‫مع‬ ‫وتتعاون‬ ‫تتفاعل‬ ‫عناصر‬ ‫مجموعة‬ ‫النظام‬
‫النظم‬ ‫أنواع‬
‫ذهني‬ ‫أو‬ ‫فيزيائي‬
‫مغلق‬ ‫أو‬ ‫مفتوح‬
‫اصطناعي‬ ‫أو‬ ‫طبيعي‬
‫الحاسوبية‬ ‫األنظمة‬
Users +Software + Hardware

3. ‫عن‬ ‫عامة‬ ‫لمحة‬
‫النمذجة‬

-
‫في‬ ً‫ا‬‫مهم‬ ً‫ا‬‫دور‬ ‫النماذج‬ ‫بناء‬ ‫و‬ ‫النمذجة‬ ‫تلعب‬
‫وفي‬ ‫االختصاصات‬ ‫مختلف‬ ‫و‬ ‫البحث‬ ‫مجاالت‬ ‫مختلف‬
‫مراحل‬ ‫مختلف‬
‫بناء‬
‫نظام‬
‫و‬
‫تطوير‬
‫تحليله‬ ‫و‬ ‫ه‬

-
‫مجاالت‬ ‫من‬ ‫مجال‬ ‫كل‬ ‫في‬
‫البحث‬
‫تقنيات‬ ‫هناك‬
‫النماذج‬ ‫لبناء‬ ‫خاصة‬
،
‫خصائص‬ ‫و‬ ‫وظائف‬ ‫مع‬ ‫تتناسب‬
‫الم‬ ‫الحالة‬
‫ن‬
‫مذجة‬

4. ‫تعاريف‬
‫النمذجة‬
‫المحاكاة‬ ‫و‬ ‫النموذج‬ ‫و‬

‫النمذجة‬
:
‫و‬ ‫فهمه‬ ‫على‬ ‫يساعدنا‬ ،‫لنظام‬ ‫نموذج‬ ‫بناء‬ ‫فن‬
ً‫ا‬‫فعلي‬ ‫بنائه‬ ‫دون‬ ‫به‬ ‫التحكم‬ ‫أو‬ ‫بالتنبؤ‬ ‫والقيام‬ ‫تصميمه‬

‫النموذج‬
:
‫على‬ ‫قدرتنا‬ ‫تحسين‬ ‫به‬ ‫يراد‬ ‫للنظام‬ ‫مبسط‬ ‫تمثيل‬ ‫هو‬
‫لمجرد‬ ‫أو‬ ‫قائم‬ ‫هو‬ ‫ما‬ ‫على‬ ‫المحافظة‬ ‫أو‬ ‫للتغيير‬ ‫الضروري‬ ‫الفهم‬
‫سلوك‬ ‫على‬ ‫السيطرة‬ ‫ربما‬ ‫أو‬ ‫تفسيره‬ ‫و‬ ‫النظام‬ ‫سلوك‬ ‫معرفة‬
‫النظام‬
.

‫المحاكاة‬
:
‫تشبيه‬ ‫عملية‬ ‫هي‬
(
‫التأثيرات‬ ‫و‬ ‫المظهر‬ ‫في‬
)
‫نموذج‬ ‫وتجريب‬ ‫ببناء‬ ‫ذلك‬ ‫و‬ ‫النظام‬ ‫سلوك‬ ‫في‬ ‫الهامة‬ ‫للمفاهيم‬
‫النظام‬
.

‫المحاكاة‬
‫الحاسوبية‬
:
‫و‬
‫و‬ ‫المظهر‬ ‫في‬ ‫تشبيه‬ ‫عملية‬ ‫هي‬
‫التأثيرات‬
‫النظام‬ ‫سلوك‬ ‫في‬ ‫الهامة‬ ‫للمفاهيم‬
‫ببناء‬ ‫ذلك‬ ‫و‬
‫النموذج‬ ‫هذا‬ ‫تجريب‬ ‫و‬ ‫الحاسوب‬ ‫في‬ ‫لمحاكاة‬ ‫مكيف‬ ‫نموذج‬
ً‫ا‬‫حاسوبي‬
.

5. ‫النماذج‬ ‫أنواع‬
:

‫نماذج‬
‫فيزيائية‬
:
‫ملموسة‬ ‫اشياء‬ ‫من‬ ‫مكونة‬

‫ذهنية‬ ‫نماذج‬

‫تدفقية‬ ‫مخططات‬ ‫نماذج‬

‫البيانية‬ ‫الرسوم‬ ‫و‬ ‫الخرائط‬ ‫نماذج‬

‫رمزية‬ ‫نماذج‬
:
‫ورياضية‬ ‫منطقية‬ ‫عالقات‬
-
‫خرائط‬
-
‫صور‬

‫الديناميكية‬ ‫النظام‬ ‫نماذج‬

‫الساكنة‬ ‫النظام‬ ‫نماذج‬

6. ‫أمثلــــــــــــة‬

‫البناء‬ ‫هندسة‬ ‫مجال‬ ‫في‬ ‫أبنية‬ ‫نماذج‬ ‫انشاء‬
‫يتطلب‬
‫استخدام‬
‫و‬ ‫بناء‬ ‫مخططات‬
‫استخدام‬
‫إحصائية‬ ‫حسابات‬
‫المطلوب‬ ‫للنموذج‬ ‫للوصول‬ ‫لألبنية‬ ‫وحسابية‬

‫النمذجة‬
‫بالغراف‬
(
(Graph
:
‫تستخدم‬
‫الطريقة‬ ‫هذه‬
‫في‬
‫نمذجة‬
‫القطا‬ ‫وسكك‬ ‫الطرق‬
‫رات‬

‫النمذجة‬
‫أو‬ ‫نظام‬ ‫مكونات‬ ‫توصيف‬ ‫في‬ ‫وتستخدم‬ ‫الرياضية‬
‫حالة‬

‫النمذجة‬
‫وصنع‬ ‫الترجمة‬ ‫مجال‬ ‫في‬ ‫وتستخدم‬ ‫باألشجار‬
‫القرار‬

‫ساكنة‬ ‫نماذج‬ ‫هناك‬
‫ديناميكية‬ ‫ونماذج‬

7. ‫من‬ ‫الهدف‬
‫النمذجة‬

‫البنى‬ ‫نمذجة‬
:
‫النموذج‬ ‫يظهر‬
‫النظام‬ ‫صفات‬
‫و‬
‫بينها‬ ‫والعالقة‬ ‫مكوناته‬
(directed graph - UML diagram)

‫السلوك‬ ‫نمذجة‬
:
‫النموذج‬ ‫يظهر‬
‫تغي‬ ‫خالل‬ ‫من‬ ‫النظام‬ ‫سلوك‬
‫حاالته‬ ‫ر‬
‫تأثيرات‬ ‫نتيجة‬ ‫أو‬ ‫للزمن‬ ‫بالنسبة‬
‫عليه‬ ‫مطبقة‬
(
UML
–Automata- Petri net )

8. ‫النموذج‬ ‫بناء‬ ‫خطوات‬

‫غموض‬ ‫بال‬ ‫و‬ ‫منطقي‬ ‫بشكل‬ ‫و‬ ‫بوضوح‬ ‫المسألة‬ ‫تحديد‬

‫الخطوات‬ ‫من‬ ‫سلسلة‬ ‫النطالق‬ ‫تؤدي‬ ‫نمذجة‬ ‫منهجية‬
‫العالقات‬ ‫كل‬ ‫فهم‬ ‫الصعب‬ ‫من‬ ‫و‬ ‫جيدة‬ ‫بمعرفة‬ ‫المنطقية‬
‫الحقيقية‬ ‫لمبادلة‬ ‫نضطر‬ ‫لذلك‬ ‫الحقيقي‬ ‫للنظام‬ ‫الداخلية‬
‫المتغيرات‬ ‫بعض‬ ‫نتخذ‬ ‫حيث‬ ‫أبسط‬ ‫بعالقات‬ ‫العمومية‬ ‫و‬
‫للنظام‬ ‫الداخلية‬ ‫العالقات‬ ‫و‬ ‫فقط‬
.

‫المتغيرات‬ ‫من‬ ‫جزئية‬ ‫مجموعة‬ ‫أصغر‬ ‫اختيار‬ ‫على‬ ‫القدرة‬
‫مرغوب‬ ‫و‬ ‫واضح‬ ً‫ا‬‫كافي‬ ‫وصفا‬ ‫الحقيقي‬ ‫النظام‬ ‫تصف‬
‫للمنمذج‬

‫التنبؤ‬ ‫التقدير‬ ‫الحدس‬ ‫الخبرة‬ ‫على‬ ‫تعتمد‬ ‫النمذجة‬ ‫مهارة‬
‫الخيال‬ ‫و‬

9. Need to Model
If original system is:
1- not observable
2- very small or very big
3- very complex
4- not exist
5- not available-

10. Need to Model
If the work with original is:
1- very dangerous
2- Very expensive
3- Impossible
4- verboten

11. Simple models of complex
world
- Newtonian Physics is a special case
of more recent models.
- We hardly travel at relativistic speed
or operate in quantum dimensions
do we? So why do not use the
simpler model?

12. Simulation
Purposes of simulation :
1. Help to understand
2. Help to observe behavior of modeled
system
3. Help to test ,valid, verificate, or evaluate
4. Help to discover mistakes
5. To simulate real world

13. Petri Nets
Concurrency and causality

14. History
Petri nets were introduced by C.A. Petri in his
PH.D. Dissertation“ Kommunikation mit
Automaten.” Bonn 1962
In models of existing systems, automata imply an
approximation. (simple, but applicable only if their
assumptions hold)
In designs of new systems, automata involve over-
specification! (engineers have to implement the
assumptions)

15. The Aim of Petri Nets (PN)
PN are graphical tool for the formal description of
the flow of activities in complex systems.
PN are particularly useful from modeling Systems
with concurrent and asynchronous processing.
Typical situations that can be modeled by PN are
distribution, synchronization, sequentiality,
concurrency and conflict.
PN are particularly suited to represent in a natural
way logical interaction among parts or activities in a
system.
PN can be modeled real or abstract automat and
engines , communication and behaviors of software
and hardware components.

16. What is Petri net?
PN is a quintuple (P,T, I,O, M) where:
P=(p1, p2, p3, …, p np ) is the set of np places (drawn
- as
circles in the graphical presentation);
T=(t11, t2, t3, …, t nt ) is the set of nt transitions (drawn
- as
bars) ;
- I is the transition input relation and is represented by
means of arcs directed from places to transitions ;
- O is the transition output relation and is represented by
means of arcs directed from transitions to places;
- M={m1,m2,m3,…,mnp} is the marking. The generic entry
m i is the number of tokens (drawn as black dots) in place p i
in marking M.
- The graphical structure of a PN is a bipartite directed graph: the
nodes belong to tow different classes (places and transitions) and
edges (arcs) are allowed to connect only nodes of different
classes ( multiple arcs are possible in the definition of the I and O
relations)

17. What is Petri net?
The dynamics of a PN is obtained by moving the
tokens in the places by means of the following
execution rules:
1. A transition is enabled in marking M if all its input
places carry at least one token;
An enabled
2. transition fires by removing one token
per arc from each input place and adding one token
per arc to each output place
Given an initial marking M1, The reachability set
R(m1) is the set of all the markings that can be
obtained by repeated application of a above rules

18. A transition is enabled in marking M if all its input places
carry at least one token
An enabled transition fires by removing one token per arc
from each input place and adding one token per arc to
each output place
tk is enabled in marking M if:
For any ` , mi ≥ 1
Marking M`, obtained from M by firing tk , is said to be
immediately reachable from M and the firing operation is
denoted by the symbol (M
tk
M`)
M` is given by the following relationship:
M`=
M(p i) +1 if pi i ϵ O(t k), pi no ϵ I (t k )
M(p i) -1 if pi no ϵ O )t k ), p i ϵ I (tk )
M(pi ) otherwise

19. Petri Nets and the Modeling of
Systems
- PN used for modeling real systems are sometimes
referred to as condition /event nets
- Places identify the condition of the parts of the system
( working, failed, idle…)
- Transitions describe the passage from one condition
to
another
An event occurs (transition fires)
-
- Occurrence of the event modifies in whole or in part
the status of the conditions (marking)
- The number of tokens in a place can be used to
identify the number of resources

20. Typical Situation of Interaction of
activities arising in system modeling
1. concurrency ( or parallelism)
In figure 1 the activities modeled by tow
transitions run concurrently
2. Synchronization
In figure 2 the Synchronization activityis
modeled by means of transitionT1
3.conflict
In figure 3 t1 and t2 are allowed to fire
concurrently, but are connected to a
shared resource (one token), that can not
be accessed by t1, t2 simultaneously.

21. Examples
CONCURRENCY SYNCHRONISATION COMMUNICATION
(1) (2) (3)
A B A B A B
t1
t2 t3

22. Examples
multiplicity/resources individuality/data
A
A B
A B
A B
conflict / choic
(4) (5) (6)
t1 t2
t3
t4

23. Weighted Petri nets
- Original Petri nets : only 1 token can be
removed/added from a place when a
transition fires (i.e. the weight is always 1)
- Weighted Petri nets:
- Generalized the original Petri nets to
allow multiple tokens to be
added/removed when a transition fires.
- The edges are labeled with the weight(
i.e. number of tokens)
-If there is no label, then the default value
is 1.

24. Mathematical definition:
P={p1, p2, ….pm} is a finite set of places
T={t1,t2…,tn } is a finite set of transitions
F ⊆(pχT) U (pχT) is a set of arcs
W: F→ {1,2,3, …} is a weighting function
M0 :P → {1,2,3,….} is the initial marking
P∩T=Ø and P UT≠Ø
Example
Petri net before transition t1 fires after t1 fires
p1
p2
p3
t1
2
4
p1
p2
p3
t1
2
4

25. Reachability
• Reachability set and Reachability
Graph R(M0)is a set of all possible
markings reachable from the initial
marking M0
• If marking M is in the reachability set
R(M0), it means that there exist a firing
sequence transforming M0 into M
• This is an useful property for analysis of
systems. We can ask whether :
A desired stat can be reached at all?
Is it possible for a system to arrive at an
undesired state (erroneous) ?

26. Reachabilty Graph
• Reachabilty can be analysed by building a
reachabiltiy graph
• Reachabilty graph is a directed Graph where
nodes represents marking and edge –transitions
between tow Markings
• The Graph is constructed by finding all
possible transition from initial marking this gives
a set of markings reachable from the initial one
then all possible transitions from the previously
discovered
• May lead to extremely large graph

27. Example : two users share printer
End print
End print
start print start print
User1-work
User1-finish User2-finish
User2-work
Printer free

28. Properties of Petri nets
• Petri nets Properties are basis for their
formal analysis
• The following Properties are
commonly used:
- Reachability
- Liveness
- Boundedness

29. Properties of Petri nets
• Liveness: A potentially firable in M if there exist
sequence of transition firings which leads to a
marking in which the transition is enabled. A
transition is live if it is potentially firable in any
marking of R(M1 ). A transition is dead in M if it is
not potentially firable; if the PN enters marking M
the dead transition can not fire any more.
• In other words every transition of the net can fire
an infinite number of times
• A Petri net PN is structurally live, if any initial
marking of PN is live
• Liveness may be used to modeled the
occurrences of
deadlocks.

30. • Safeness
A place is safe if the token count does not exceed 1
in any marking of R(M1 ). A PN is safe if each place is
safe.
• Boundedness
A simple generalization of safeness is the concept of
boundedness. A place is bounded with bound k, if
the token count does not exceed k in any marking of
R(M1 ). A PN is k- bounded if each place is k-
bounded.
• Conservation
APN is strictly conservative if the total number of
tokens is constant in each Marking of R(M1).

31. High level Petri nets
• Petri nets have been extended over the year in
many
directions including time.
Hierarchical Petri nets :
• developed in the late 1980s
• Specifications for real systems have a tendency to
become large and complex
• An Abstraction mechanism, hierarchical structuring
reviewing and modifying the model easier
• The hierarchical construct is called a subnet
• A subnet is an aggregate of a number of places
transitions, and subsystem
Such a construct can be used to structure large
processes
• At one level we want to give a simple description of
the process (without having to consider all details).
• Another level we want to specify a more detailed
| behavior.

32. 2. Coloured Petri Nets
• Developed in the late 1970s
K. Jensen, “colored Petri nets and invariant
method”
Theoretical computer science, volume 14, 1981.PP
317-336.
• Token often present objects (e.g. resources, goods,
humans) in the modeled system
• To represent attributes of these objects, the Petri
nets model is extended with colored or typed tokens
• Each token has a value often referred to as a color
• Transitions use the values of the consumed token to
determine the values of the produced tokens
• Transition describes the relation between the
values of the input tokens and the values of the
output tokens
It is also possible to specify preconditions which take
the color of tokens to be consumed into account

33. An overview of Performance
Evaluation
• Computer system users, administrators ,and designers
are all interested in Performance Evaluation
• Goal: the highest Performance at the lowest cost
The computer industry is becoming more competitive
Search the best cost - Performance
• Need to Performance Evaluation at every stage in life
cycle of computer system ( design- manufactoring-
sales/purchase-use- upgrade…)
• Designer compare number of alternatives designs to
find best
Even no alternatives to help in determining how well it is
performing, improvement need to be made
First to Performance Evaluation select ( right measure of
Per., right measurement environment, and right
techniques

34.  The use of M&S within engineering is well
recognized. Simulation technology belongs to
the tool set of engineers of all application
domains and has been included in the body
of knowledge of engineering management.
M&S helps to reduce costs, increase the
quality of products and systems, and
document and archive lessons learne