More Related Content
PDF
PDF
『ビッグデータ時代を勝ち抜くデータマネジメント』 セミナー資料 PDF
Rを用いたLTV(Life Time Value)の推定 PDF
#みどりぼん 11章「空間構造のある階層ベイズモデル」後半 PDF
分析のビジネス展開を考える―状態空間モデルを例に @TokyoWebMining #47 PDF
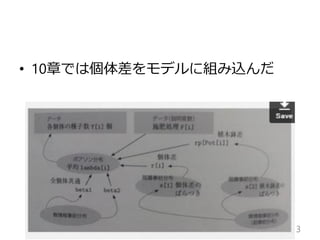
データ解析のための統計モデリング入門10章前半 PDF
ベイジアンモデリングによるマーケティングサイエンス〜状態空間モデルを用いたモデリング PDF
【3時間で学ぶ! �スモールサクセス型�『カスタマージャーニー分析』】 slideshare公開用 Similar to みどりぼん第11回 前半
PDF
PDF
PPTX
PDF
PPTX
NagoyaStat #5 データ解析のための
統計モデリング入門 第10章 PDF
PDF
PDF
Rでベイズをやってみよう!(コワい本1章)@BCM勉強会 PDF
続わかりやすいパターン認識11章(11.1 - 11.4) PDF
データ解析のための統計モデリング入門3章後半 PDF
【Zansa】第12回勉強会 -PRMLからベイズの世界へ PPTX
PDF
Stanの紹介と応用事例(age heapingの統計モデル) PDF
PDF
PPTX
【読書会資料】『StanとRでベイズ統計モデリング』Chapter12:時間や空間を扱うモデル PDF
PDF
PPTX
【招待講演】パラメータ制約付き行列分解のベイズ汎化誤差解析【StatsML若手シンポ2020】 PDF
More from Atsushi Hayakawa
PDF
PDF
PDF
dataclassとtypehintを使ってますか? PDF
トライアスロンとgepuro task views V2.0 Japan.R 2018 PPTX
PPTX
Analyze The Community Of Tokyo.R PPTX
PDF
PDF
simputatoinで欠損値補完 - Tokyo.R #65 PDF
PPTX
PPTX
Rstudio上でのパッケージインストールを便利にするaddin4githubinstall PDF
PDF
Splatoon界での壮絶な戦い&Japan.Rの宣伝 PDF
PDF
PDF
nginxのログを非スケーラブルに省メモリな方法で蓄積する PDF
PDF
PDF
みどりぼん第11回 前半
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
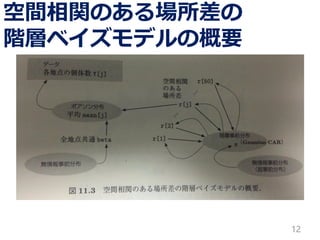
Intrinsic GaussianCARと呼ばれる
11.2.2空間構造のある階層事前分布
•푝푟푗|휇푗,푠= 푛푗 2휋푠2exp− 푟푗−휇푗 22푠2/푛푗
•平均휇푗= 푟푗−1+푟푗+12
•標準偏差: 푠 푛푗 , 푛푗は近傍数
•左右の両端푗=1,푗=50
–휇1=푟2,휇50=푟49
9
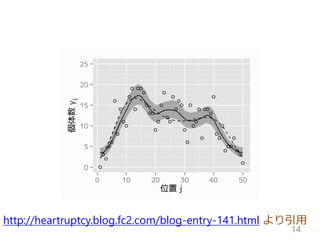
ある区画はそれと接している区画とだけ
相互作用すると仮定 - 10.
- 11.
- 12.
- 13.
- 14.
- 15.