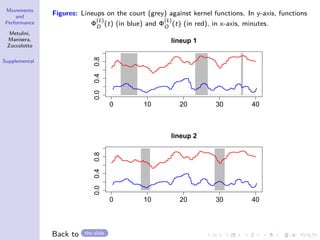
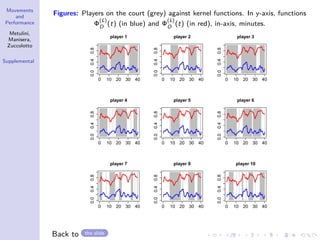
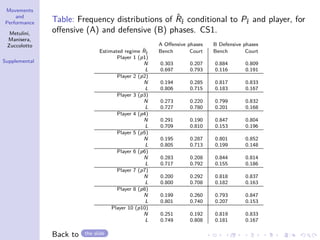
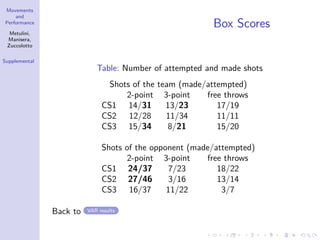
The document discusses the modeling of dynamic patterns of surface area in basketball and their impact on team performance using statistical methods. It aims to analyze how player positioning affects both offensive and defensive plays, employing a Markov switching model and various data processing techniques. The findings indicate differing regime behaviors during different phases of the game and suggest avenues for further research on player trajectories and tactical influences.

1. Movements
and
Performance
Metulini,
Manisera,
Zuccolotto
Context
Data
Methods &
Results
Conclusions
Acknowledgm.
& References
Quote of the day:
If the world were a team, it would be a better
place, because every man would import
something of the player next to him
(Larry Brown, Coach Torino Basket)

2. Movements
and
Performance
Metulini,
Manisera,
Zuccolotto
Context
Data
Methods &
Results
Conclusions
Acknowledgm.
& References
Modelling the dynamic pattern of surface area
in basketball and its effects on team
perfomance1
1
Online First in Journal of Quantitative Analysis in Sports
Rodolfo Metulini, Marica Manisera & Paola Zuccolotto
University of Brescia - Department of Economics and Management
Iasi - August 28th, 2018

3. Movements
and
Performance
Metulini,
Manisera,
Zuccolotto
Context
Data
Methods &
Results
Conclusions
Acknowledgm.
& References
Table of contents
1 Context
2 Data
3 Methods & Results
4 Conclusions
5 Acknowledgm. & References

4. Movements
and
Performance
Metulini,
Manisera,
Zuccolotto
Context
Data
Methods &
Results
Conclusions
Acknowledgm.
& References
Background & Motivation
late 90s: first examples of statitical methods proposed ad-hoc
for specific sport problems (e.g. Duckworth-Lewis-Stern - DLS,
method using in resetting targets in limited overs cricket)
(Duckworth and Lewis 1998, 2004, Stern 2016).
2000s: increasing availability of big & open data (e.g. GPS)
2003: Moneyball thinking (Lewis 2003)
2017: I think that the best sports statistics contributions have
two components: (1) they contain statistical novelty and (2)
they address a real sporting problem (Tim B. Swartz - Where
Should I Publish my Sports Paper? - The American Statistician)

5. Movements
and
Performance
Metulini,
Manisera,
Zuccolotto
Context
Data
Methods &
Results
Conclusions
Acknowledgm.
& References
Aims
To find whether certain patterns of space among players affect
team performance, from both an offensive and a defensive
perspective
We focus on the time series dynamics of basketball players’ coordinates , with
a two-fold purpose:
• To give tools allowing a detailed description and analysis of a
game with respect to surface areas dynamics,
• to investigate its influence on the points made by both the team
and the opponent

6. Movements
and
Performance
Metulini,
Manisera,
Zuccolotto
Context
Data
Methods &
Results
Conclusions
Acknowledgm.
& References
(Weakly-) related Literature in
Basketball
• Outlining the main features of a game by means of
descriptive statistics (Kubatko et al. 2007),
• forecasting the outcome of a game or a tournament (West
2008; Brown et al. 2010; Gupta 2015; Lopez and Matthews 2015; Ruiz
and Perez-Cruz 2015; Yuan et al. 2015; Manner 2016),
• analysing players’ performance (Page, Fellingham, and Reese
2007; Cooper, Ruiz, and Sirvent 2009; Fearnhead and Taylor 2011; Page,
Barney, and McGuire 2013; Deshpande and Jensen 2016),
• identifying optimal game strategies (Annis 2006) and
describing the players’ reactions to stressful moments.
(Crocker and Graham 1995; Zuccolotto, Manisera, and Sandri 2017).

7. Movements
and
Performance
Metulini,
Manisera,
Zuccolotto
Context
Data
Methods &
Results
Conclusions
Acknowledgm.
& References
(Strictly-) related Literature
(1) to measure a player’s performance vs. (2) to assess the
impact of the player on the teammates’ behavior and on the
team’s performance
point (2) is still little explored:
• Lamas et al. (2011) : some players’ profile may influence the
recurrence of some team game strategy (e.g. create empty
space for scoring opportunities),
• Fewell et al. (2012) describe the interactions among
individuals to determine the associated with team
advancement.

8. Movements
and
Performance
Metulini,
Manisera,
Zuccolotto
Context
Data
Methods &
Results
Conclusions
Acknowledgm.
& References
Empirical Strategy
We propose a three-step procedure integrating different statistical
modelling approaches. Specifically:
• We first employ a Markov Switching Model (MSM) to detect
structural changes in the surface area;
• we perform descriptive analyses in order to highlight
associations between regimes and relevant game variables;
• we assess the relation between the regime probabilities and the
scored points by means of Vector Auto-Regressive (VAR)
models.

9. Movements
and
Performance
Metulini,
Manisera,
Zuccolotto
Context
Data
Methods &
Results
Conclusions
Acknowledgm.
& References
Data Source
• Tracked data refer to 3 professional games played in February 2017 at the
Italian Basketball Cup Final Eight. Data provided by MYagonism ,
• each player worn a microchip, collecting the position (P, 30 cm2 accuracy),
velocity (V) and acceleration (A) in the x-axis (court length), y-axis (court
width), and z-axis (height),
• sampling frequency of about 50 Hz,
• a total of 10 (for CS1 and CS3) and 11 (for CS2) tracked players,
• the system records a set of about 500m measurement per game-team,
• play-by-play data are not available for this tournament, so, we use box
score information and we collected the scores of the match at the end of
every minute, by watching the video of the game.

10. Movements
and
Performance
Metulini,
Manisera,
Zuccolotto
Context
Data
Methods &
Results
Conclusions
Acknowledgm.
& References
Data Processing
• data are detected with a non-constant frequency,
• data of different players are recorded at different time instants.
We regularized time instants, creating a dataset with any detected
time instant, and we attribute the last datum available to players not
detected in that time instant.
• However, the dataset (X) considers the full game length.
We cleaned it by dropping inactive moments, according to our
filtering procedure
• The final dataset (Xr) for team 1 counts for 206,332 rows,
team 2 counts for 232,544 rows, while team 3 counts for
201,651 rows (Frequency: 80/90 Hz).

11. Movements
and
Performance
Metulini,
Manisera,
Zuccolotto
Context
Data
Methods &
Results
Conclusions
Acknowledgm.
& References
Filtering Procedure
From: Metulini, R., Filtering procedures for sensor data in basketball. Statistics & Applications. 2017-2
Full data matrix X (nrow = T);
↓
1-A Remove row if players on the court = 5
↓
1-B Remove row if a player is on the free throw circle
↓
1-C Remove row if players veloc-
ity < h2 for h3 consecutive seconds
↓
Reduced data matrix (nrow = T’ ≤ T)
↓
2-A Assign offense or defense labels
↓
2-B Assign actions’ sorting
↓
Reduced data matrix with actions’ labelling and sorting

12. Movements
and
Performance
Metulini,
Manisera,
Zuccolotto
Context
Data
Methods &
Results
Conclusions
Acknowledgm.
& References
Step 1: regime-switching surface
areas1
• Of particular interest to economists is the tendency of many variables
to behave differently during economic downturns, shocks, breaks,
etc..
• translating the idea into team sports, we assume that players’ surface
area behaves differently in different moments.
We model the surface area as a 2-regimes (Narrow, N and Large, L) time
series process involving different mean levels, using a Markov Switching
Model (MSM; Hamilton 2010)
C˜t : convex hull of the five players on the court at time ˜t
A˜t : the corresponding area
R˜t : the (unobserved) random variable denoting the regime at time ˜t
1
we regularized the space between consecutive observations by selecting from
Xr a row every 100 milliseconds. We call these time instants as ˜t

13. Movements
and
Performance
Metulini,
Manisera,
Zuccolotto
Context
Data
Methods &
Results
Conclusions
Acknowledgm.
& References
Step 1: regime-switching surface
areas II
E(A˜t |R˜t = r) = α(r)
, r = N, L.2
(1)
The probabilistic model describing the regimes’ dynamics is a two-state
Markov chain (Hamilton, 1989),
Pr(R˜t |R˜t−1, R˜t−2, . . .) = Pr(R˜t |R˜t−1). (2)
We denote with πNN = Pr(R˜t = N|R˜t−1 = N), πLL = Pr(R˜t = L|R˜t−1 = L)
the two-state transition probabilities, with πNL = 1 − πLL, πLN = 1 − πNN .
N(α(N)
, σ2
N ), N(α(L)
, σ2
L) are the Gaussian densities under the two regimes.
The parameter vector θ = (α(N)
, α(L)
, σ2
N , σ2
L, πNN , πLL) is estimated via
EM algorithm.
2
Formulation is the simplest assumption in the family of regime-switching
models, which can assume also the presence of autoregressive components or the
effect of some exogenous variables.

14. Movements
and
Performance
Metulini,
Manisera,
Zuccolotto
Context
Data
Methods &
Results
Conclusions
Acknowledgm.
& References
Step 2: analysis of the regimes’
dynamics
We investigate the connections between the regimes and P˜t .
Let P˜t be the categorical variable denoting the game phase, with categories
p = O, D, Tr (offense, defense and transition, respectively)
We find a prevalence of regime r = N in defense and a corresponding
prevalence of r = L in offense3
.
However, we are more interested to identify departures from this evidence
by plotting the kernel functions
Φ(r)
p (t) = φ
˜t:P˜t =p
ξ
(r)
˜t
4
(3)
with respect to the presence/absence of a specific lineup or players on the
court, also with respect to game phases
3
Contingency tables confirmation: in CS1 82.4% of the times in defense
correspond to regime r = N, 77.3% of the times in offense to regime r = L
4
φ(·) is a Nadaraya-Watson kernel regression (Nadaraya1964; Watson1964).
ξ
(r)
˜t
= Pr(R˜t = r|I˜t , θ)

15. Movements
and
Performance
Metulini,
Manisera,
Zuccolotto
Context
Data
Methods &
Results
Conclusions
Acknowledgm.
& References
Step 3: relationship between the
regimes and the points scored
SPteam
¯t and SPopp
¯t
: points scored by the team and the opponents, in the
time interval (¯t − 1,¯t], where ¯t = 1, 2, · · · ,¯t express minutes.
Yteam,L
¯t
and Yopp,N
¯t
are the vectors
Yteam,L
¯t
=
SPteam
¯t
ΦL
O(¯t)
and Yopp,N
¯t
=
SPopp
¯t
ΦN
D(¯t)
, (4)
We assume a VAR model (Sims 1980):
Yteam,L
¯t
= η0 + η1Yteam,L
¯t−1
+ · · · + ηqYteam,L
¯t−q
+ εteam,L
¯t
(5)
Yopp,N
¯t
= ω0 + ω1Yopp,N
¯t−1
+ · · · + ωs Yopp,N
¯t−s
+ εopp,N
¯t
, (6)
η0, ω0: 2 × 1 vectors of the intercepts,
η1 ... ηq, ω1 ... ωs : 2 × 2 matrices of the coefficients,
εteam,L
¯t
, εopp,N
¯t
are the innovation processes.

16. Movements
and
Performance
Metulini,
Manisera,
Zuccolotto
Context
Data
Methods &
Results
Conclusions
Acknowledgm.
& References
Step 3: relationship between the
regimes and the points scored II
Orders of the VAR models:
• we adopt Bayesian Information Criterion (BIC), that suggests to set
q = 1 and s = 1 in both CS1 and CS3. For CS2, instead, we should
opt for q = 3 and s = 2;
• the differences between the BIC values for order 1 and the optimal
one is very low. According to Kass 1995, this denotes an evidence
against the higher BIC’s model;
• in order to ensure comparability of results, we set q = 1 and s = 1
also for CS2.
We fit model (5) and model (6) in the form:
Yteam,L
¯t
= η0 + η1Yteam,L
¯t−1
+ εteam,L
¯t
(7)
Yopp,N
¯t
= ω0 + ω1Yopp,N
¯t−1
+ εopp,N
¯t
, (8)

17. Movements
and
Performance
Metulini,
Manisera,
Zuccolotto
Context
Data
Methods &
Results
Conclusions
Acknowledgm.
& References
Discussion
• Starting from the evidence that surface area switches from narrow to
large when moving from defense to offense, we inspect the dynamic
of surface areas during a game;
• the association of N-L regimes to D-O phases does not perfectly
match. This stimulated a deeper investigation on the occurrence of
regime N and L with respect to game variables;
• we defined smoothed functions that allow graphical inspection of the
regimes during offense and defense;
• the relation between regimes’ and the points scored by the team and
the opponent seem to be genuinely match-specific. This can be
justified in view of the different tactics decided by coaches.

18. Movements
and
Performance
Metulini,
Manisera,
Zuccolotto
Context
Data
Methods &
Results
Conclusions
Acknowledgm.
& References
Future research
• To jointly analyse the trajectories of the players of both the
team and the opponent;
• to introduce the ball trajectory and measure its role on the
relationship between surface area and performance;
• to include the dimension of coaches’ tactics in the context of a
three-dimensional analysis covering game strategy, players’
movements and team performance.

19. Movements
and
Performance
Metulini,
Manisera,
Zuccolotto
Context
Data
Methods &
Results
Conclusions
Acknowledgm.
& References
Acknowledgements
Projects
Big & Open Data Innovation (BODaI) laboratory BODaI
Big Data analytics in Sports (BDsports) laboratory BDsports
People
Raffaele Imbrogno (Foro Italico University, Roma IV)
Paolo Raineri (MYagonism)
Tullio Facchinetti (University of Pavia)
Giuseppe Arbia (Catholic University of the Sacred Heart)
Marcello Chiodi (University of Palermo)

20. Movements
and
Performance
Metulini,
Manisera,
Zuccolotto
Context
Data
Methods &
Results
Conclusions
Acknowledgm.
& References
Selected Publications
Gudmundsson, J., & Horton, M. (2017). Spatio-temporal analysis of team sports.
ACM Computing Surveys (CSUR), 50(2), 22.
Hamilton, J. D. (2010). Regime Switching Models. Pp. 202-209, in
Macroeconometrics and Time Series Analysis. London: Palgrave Macmillan.
Lamas, L., D. D. R. Junior, F. Santana, E. Rostaiser, L. Negretti, and C.
Ugrinowitsch (2011). Space Creation Dynamics in Basketball Offence: Validation
and Evaluation of Elite Teams. International Journal of Performance Analysis in
Sport 11(1):71-84.
Metulini, R., M. Manisera, and P. Zuccolotto (2017). Sensor Analytics in
Basketball. Proceedings of the 6th International Conference on Mathematics in
Sport.
Metulini, R., Manisera, M., & Zuccolotto, P. (2018) Modelling the dynamic
pattern of surface area in basketball and its effects on team performance. Journal
of Quantitative Analysis in Sports. Online First.

21. Movements
and
Performance
Metulini,
Manisera,
Zuccolotto
Supplemental
Table: Markov Switching Model results (A), 95% confidence intervals
for the estimated intercepts (B) and transition probabilities (C)
(A)
CS1 CS2 CS3
Regime N Coef (S.e.) Coef (S.e.) Coef (S.e.)
Intercept 22.060*** 24.448*** 21.940***
(0.114) (0.123) (0.112)
Residual standard error 9.156 9.328 8.760
Regime L Coef (S.e.) Coef (S.e.) Coef (S.e.)
Intercept 62.897*** 60.857*** 56.114***
(0.221) (0.265) (0.220)
Residual standard error 21.087 20.256 18.133
(B)
95% confidence intervals for the estimated intercepts
CS1 CS2 CS3
Regime N 21.835; 22.284 24.207; 24.689 21.721; 22.160
Regime L 62.465; 63.329 60.337; 61.376 55.683; 56.545
(C)
Transition probabilities
CS1 CS2 CS3
0.986 0.013
0.014 0.987
0.987 0.018
0.013 0.982
0.986 0.013
0.014 0.987
5
Back to the slide
5
persistence index of about 7/8 seconds

22. Movements
and
Performance
Metulini,
Manisera,
Zuccolotto
Supplemental
Figures: Lineups on the court (grey) against kernel functions. In y-axis, functions
Φ
(L)
D
(t) (in blue) and Φ
(L)
O
(t) (in red), in x-axis, minutes.
0 10 20 30 40
0.00.40.8
lineup 1
0 10 20 30 40
0.00.40.8
lineup 2
Back to the slide

23. Movements
and
Performance
Metulini,
Manisera,
Zuccolotto
Supplemental
Figures: Players on the court (grey) against kernel functions. In y-axis, functions
Φ
(L)
D
(t) (in blue) and Φ
(L)
O
(t) (in red), in-axis, minutes.
0 10 20 30 40
0.00.40.8
player 1
0 10 20 30 40
0.00.40.8
player 2
0 10 20 30 40
0.00.40.8
player 3
0 10 20 30 40
0.00.40.8
player 4
0 10 20 30 40
0.00.40.8
player 5
0 10 20 30 40
0.00.40.8
player 6
0 10 20 30 40
0.00.40.8
player 7
0 10 20 30 40
0.00.40.8
player 8
0 10 20 30 40
0.00.40.8
player 10
Back to the slide

24. Movements
and
Performance
Metulini,
Manisera,
Zuccolotto
Supplemental
Table: Frequency distributions of ˆR˜t conditional to P˜t and player, for
offensive (A) and defensive (B) phases. CS1.
A Offensive phases B Defensive phases
Estimated regime ˆR˜t Bench Court Bench Court
Player 1 (p1)
N 0.303 0.207 0.884 0.809
L 0.697 0.793 0.116 0.191
Player 2 (p2)
N 0.194 0.285 0.817 0.833
L 0.806 0.715 0.183 0.167
Player 3 (p3)
N 0.273 0.220 0.799 0.832
L 0.727 0.780 0.201 0.168
Player 4 (p4)
N 0.291 0.190 0.847 0.804
L 0.709 0.810 0.153 0.196
Player 5 (p5)
N 0.195 0.287 0.801 0.852
L 0.805 0.713 0.199 0.148
Player 6 (p6)
N 0.283 0.208 0.844 0.814
L 0.717 0.792 0.155 0.186
Player 7 (p7)
N 0.200 0.292 0.818 0.837
L 0.800 0.708 0.182 0.163
Player 8 (p8)
N 0.199 0.260 0.793 0.847
L 0.801 0.740 0.207 0.153
Player 10 (p10)
N 0.251 0.192 0.819 0.833
L 0.749 0.808 0.181 0.167
Back to the slide

25. Movements
and
Performance
Metulini,
Manisera,
Zuccolotto
Supplemental
Table: VAR model Yteam,L
¯t
= η0 + η1Yteam,L
¯t−1
+ εteam,L
¯t
CS1 CS2 CS3
Results for equation SPteam
¯t
:
Coef (S.e.) Coef (S.e.) Coef (S.e.)
SPteam
¯t−1
-0.032 -0.281 . 0.043
(0.159) (0.157) (0.169)
Φ
(L)
O
(¯t − 1) 7.951 . 4.323 7.394 .
(4.570) (3.230) (3.649)
intercept 2.194*** 2.252*** 1.649***
(0.433) (0.416) (0.402)
Results for equation Φ
(L)
O
(¯t):
Coef (S.e.) Coef (S.e.) Coef (S.e.)
SPteam
¯t−1
-0.005 0.004 -0.008
(0.006) (0.008) (0.008)
Φ
(r)
O
(¯t − 1) 0.258 0.235 0.073
(0.162) (0.164) (0.177)
intercept 0.012 -0.012 0.019
(0.015) (0.021) (0.020)
Go to the box score
Back to the slide

26. Movements
and
Performance
Metulini,
Manisera,
Zuccolotto
Supplemental
Table: VAR model Yopp,N
¯t
= ω0 + ω1Yopp,N
¯t−1
+ εopp,N
¯t
CS1 CS2 CS3
Results for equation SP
opp
¯t
:
Coef (S.e.) Coef (S.e.) Coef (S.e.)
SP
opp
¯t−1
-0.119 0.054 0.029
(0.170) (0.159) (0.162)
Φ
(N)
D
(¯t − 1) 1.610 7.934 -3.590
(4.322) (5.285) (3.688)
intercept 2.436*** 1.740*** 1.586***
(0.448) (0.400) (0.357)
Results for equation Φ
(N)
D
(¯t):
Coef (S.e.) Coef (S.e.) Coef (S.e.)
SP
opp
¯t−1
-0.016* -0.012* -0.011
(0.006) (0.005) (0.007)
Φ
(N)
D
(¯t − 1) 0.247 0.180 -0.038
(0.156) (0.169) (0.161)
intercept 0.012 -0.012 0.019
(0.016) (0.013) (0.016)
Go to the box score
Back to the slide

27. Movements
and
Performance
Metulini,
Manisera,
Zuccolotto
Supplemental
Global Positioning Systems (GPS)
Players’ coordinates have been retrieved using GPS techniques:
• Object trajectories are captured using optical- or device-tracking and
processing systems,
• the adoption of this technology and the availability of data is driven by
various factors, particularly commercial and technical.
Multivariate analysis in conjunction with GPS tracked data:
• Metulini, Manisera, and Zuccolotto 2017a) 2017b) identify patterns of
movements in basketball by means of an integration of multidimensional
scaling and cluster analysis,
• The complex system of the interactions among players is also studied by
Richardson et al. (2012) using cluster phase analysis.
Back to the slide

28. Movements
and
Performance
Metulini,
Manisera,
Zuccolotto
Supplemental
Play-by-play
Play-by-play (or event-log) reports a sequence of relevant events that
occur during a match.
• Players’ events (shots, fouls)
• Technical events (time-outs, start/end of the period)
In this work, play-by-play data are available at a limited extent only.
• Box-score
• Video analysis
Back to the slide

29. Movements
and
Performance
Metulini,
Manisera,
Zuccolotto
Supplemental
Surface Area
• with the term surface area literature defines the team spread at time
t and its effective playing space 6
• team in possession of the ball should increase surface area, while the
opponent should defend by reducing surface area (Ara´ujo and
Davids 2016),
• Surface area in the literature (Frencken et al., 2011; Moura et al.,
2012; Fonseca et al., 2012; Travassos et al., 2012),
• Visual analysis as a preliminary evidence of surface area patterns.
(Ther´on and Casares 2010; Kowshik, Chang, and Maheswaran
2012; Metulini 2016)
Back to the slide
6
according to Passos, Ara´ujo, and Volossovitch (2016), we use the area of
the convex hull.

30. Movements
and
Performance
Metulini,
Manisera,
Zuccolotto
Supplemental
Box Scores
Table: Number of attempted and made shots
Shots of the team (made/attempted)
2-point 3-point free throws
CS1 14/31 13/23 17/19
CS2 12/28 11/34 11/11
CS3 15/34 8/21 15/20
Shots of the opponent (made/attempted)
2-point 3-point free throws
CS1 24/37 7/23 18/22
CS2 27/46 3/16 13/14
CS3 16/37 11/22 3/7
Back to VAR results