The document discusses a data-driven analysis method for understanding multi-agent trajectories in team sports, highlighting the challenges in modeling complex interactions among players. It emphasizes the need for bridging theory-based and data-driven approaches to analyze team behavior effectively, mentioning the use of machine learning for trajectory prediction and classification. Additionally, it presents various methods aimed at improving the understanding of team dynamics through interpretable classification and policy modeling.

1. Data-driven Analysis for Multi-agent
Trajectories in Team Sports
2021/3/17
17th AIP Open Seminar
Structured Learning Team
Keisuke Fujii
Graduate School of Informatics, Nagoya University
Structured Learning Team, RIKEN AIP
JST Presto
Keisuke Fujii, Data-driven Analysis for Understanding Team Sports Behaviors,
Journal of Robotics and Mechatronics, to appear. https://arxiv.org/abs/2102.07545

2. Outline
1. Biography
2. General background
3. Theory-based data-driven approaches
a. Physically-interpretable classification using Graph DMD
b. Generating trajectory using policy modeling with partial
observation and mechanical constraints
4. Conclusion
2

3. Biography (Keisuke Fujii)
2010 - 2014 Graduated students (JSPS DC1), Human and
Environmental Studies, Kyoto University (Human motor control)
2014 - 2017 Post-doctoral Fellow (JSPS PD), Research Center of
Health Physical Fitness and Sports, Nagoya University
(Team sports science)
2017 - 2019 Research Scientist, RIKEN AIP (Machine learning)
2019- Assistant Professor, Graduate School of Informatics,
Nagoya University (Machine learning)
2019- Visiting Scientist, RIKEN AIP(Machine learning)
3

4. Multi-agent trajectories
We aim to reveal the principles behind the measured data, but
it is often difficult to model them due to higher-order interactions
[Gupta+18]
Animals
（sardines）
Children
[Ichikawa+18]
Athletes
[Fujii+16]
Pedestrians
4

5. Why do we model multi-agent behaviors? (e.g., team sports)
• Player position data can be recently measured in actual games
• However, team tactics are analyzed based on watching videos, etc.
• This is because team tactics are difficult to model, predict & control
Video editing software
(Sportscode)
Play freq. analysis
(Synergy)
Player & ball position (SportVU)
introduce
automate
If automated, expected to reduce the workload on experts
& to promote the understanding of audiences and beginners
5

6. Social force model, Yokoyama+18, PRE
Theory-based and data-driven approaches for modeling
Theory-based (equation-based) Data-driven (equation-free)
☺ understand
mechanism
 complex
model
☺ complex
model
 understand
mechanism
(deductive)
Simulation
Test hypothesis
gap
To analyze real-world agents, a
data-driven method to extract
principles (e.g. dynamics) will
be needed
(inductive)
e.g. Machine
learning
Prediction
Validate models
Classify based on dynamics, Fujii+18,+19
6

7. Categories of approaches for the analysis
1. using conventional
hand-crafted features
model-driven data-driven
Based on theory or experiments
Based on (machine) learning
2. conventional model-
driven approach
3. data-driven modeling
5. learning-based
forward modeling
Google research football
StarCraft II
4. theory-based
data-driven
modeling
7

8. 3. data-driven approaches in team sports analysis
Extract global spatiotemporal dynamics in actual games
8
☺ less specific knowledge, obtain global and general properties
Many methods have been proposed (surveyed in [Fujii, 21] arXiv:2102.07545)
Motion
data
Feature/representation
learning
Classification/
Regression
Label /
Motion
prediction
Motion
data
calc. kernel
(similarity)
Classification
Label
prediction
Example: motion classification and score prediction [Fujii+17; 18]
compute DMD
Although many methods have been proposed, what kinds of
methods are needed for understanding the sports behaviors?

9. 4. Theory-based data-driven modeling
To understand the behaviors, bridging theory-based and data-
driven approaches is needed: what kind of nonlinear data-driven
model will enable a better quantitative understanding?
9
In multi-agent sports behaviors, for example:
1. extracting mathematical structures (physical science)
2. modeling the components of multi-agent systems and
generating plausible movements (behavioral science)
Data-driven models that contribute to science [Cichy & Kaiser, 19]
1. predict and explain phenomena
2. serve as a starting point for establishment of new theories
will enable a better scientific understanding

10. Outline
1. Biography
2. General background
3. Theory-based data-driven approaches
a. Physically-interpretable classification using Graph DMD
b. Generating trajectory using policy modeling with partial
observation and mechanical constraints
4. Conclusion
10
Keisuke Fujii, Naoya Takeishi, Motokazu Hojo, Yuki Inaba & Yoshinobu
Kawahara, Physically-interpretable classification of network dynamics for
complex collective motions, Scientific Reports, 10, 3005, 2020
Codes: https://github.com/keisuke198619/GraphDMD

11. DMD as physically-interpretable feature extraction
Exact DMD algorithm [Tu+14] (one of the basic DMDs):
Input : matrices 𝑿 = [𝒚0, … , 𝒚𝜏−1] and 𝒀 = 𝒚1, … , 𝒚𝜏 from time-series 𝒚𝒕
Output: DMD eigenvalue 𝜆𝑗(freq. 𝜔𝑗), DMD mode 𝝍𝑗, initial value 𝑏𝑗,0
1. for stable computation, perform SVD: 𝑿 ≈ 𝑼𝜮𝑽∗
2. project 𝑭 onto space spanned by 𝑼: ෡
𝑭 = 𝑼∗
𝑭𝑼
3. compute eigenvalue 𝜆𝑗 and eigenvector 𝒘𝑗
4. obtain DMD mode 𝝍𝑗= 𝜆𝑗
−1
𝒀𝑽𝜮−1
𝒘𝑗 and 𝑏𝑗,0 = 𝝍𝑗
†𝒚0
11
Basic idea is eigen-decomposition of 𝑭 = 𝒀𝑿† († is pseudo inverse)
𝑿 =
𝑦1,1 ⋯ 𝑦𝜏−1,1
⋮ ⋮
𝑦1,𝑝 ⋯ 𝑦𝜏−1,𝑝
𝒀 =
𝑦2,1 ⋯ 𝑦𝜏,1
⋮ ⋮
𝑦2,𝑝 ⋯ 𝑦𝜏,𝑝
DMD
(continuation from Prof. Kawahara’s talk)

12. Background of Graph DMD [Fujii & Kawahra 19, Neural Networks]
Previous： Apply DMD in RKHS [Kawahara 16] to time-varying
collective motion, and develop a classification method using
spectral kernel [Fujii+ 17]
Problem：
1. kernel method is highly expressive,
but difficult to interpret the modes
due to decomposition in feature spaces
2. The motions can be represented as
network dynamics, but it did not
reflect its graph structures
→we propose Graph DMD [Fujii & Kawahra 19]
for interpretable classification Classification
Decomposed modes
Graph DMD
12
Network
dynamics
𝑡

13. Related work in network science
Complex systems can be modeled as networks using graphs
✓ Sociology, epidemiology, neuroscience, physics, chemistry, etc.
• focused on network property, classification, prediction, and control
✓ Previous methods did not extract dynamical property of network dynamics
In our proposed Graph DMD:
1. Formulate as graph dynamical systems in observed space
2. Utilize adjacency matrix series structures
13
Undirected graph
from Wikipedia
node
edge
Example of graph
dynamical systems
[Shirado+17]
order-3 tensor (node × node × time)
→should not be decomposed as a matrix

14. Graph DMD Algorithm [Fujii and Kawahara 19, Neural Networks]
Input：
1. Decomposition of after metricizing of (by tensor-train decomposition)
2. Compute pseudo-inverse of
3. Compute approximation of the Koopman operator
4. Obtain by eigendecomposition of
5. Obtain DMD modes
M is a projected matrix in
the direction that reflects
data property
similar to SVD but completely
different (reflect tensor structure)
We proposed more
straightforward
formulation (c.f.
Klus+16) using
In Graph DMD,
14

15. Physically and semantically interpretable classification
15
Input: sequence of
(sorted) adjacency matrices
It becomes 0.5 when
the distance is 1.5m
For time-varying dynamics,
we used sliding windows
[Brunton+16]
(2 s interval and 1 s overlap)

16. Comparisons with conventional methods
Task 1: team-defense classification (zone or person-to-person)
Task 2: team-offense classification (w/ or w/o cooperative play)
16
Task 1
defense
strategy
Task 2
offense
strategy （ours）
[Zhang+18, AAAI]
[Lin+18, AAAI]
[Fujii+17; 18]
[Tu+14]
In both tasks, our proposed methods were validated by better
performances than baselines

17. 17
Zone DF Person-to-person
Interpretation of extracted features
w/o cooperation
with cooperation
☺ automatically extract global and interpretable features
Team defense
Team offense

18. Outline
1. Biography
2. General background
3. Theory-based data-driven approaches
a. Physically-interpretable classification using Graph DMD
b. Generating trajectory using policy modeling with partial
observation and mechanical constraints
4. Conclusion
18
Keisuke Fujii, Naoya Takeishi, Yoshinobu Kawahara & Kazuya Takeda, Policy
learning with partial observation and mechanical constraints for multi-
person modeling, arXiv preprint arXiv:2007.03155, 2020
Codes: https://github.com/keisuke198619/PO-MC-DHVRNN

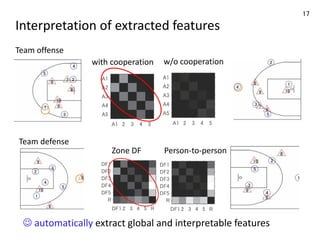
19. Data-driven agent-based modeling
Generate trajectory in actual games by e.g. time-series modeling/
reinforcement learning / imitation learning
19
☺ long-term prediction using actual data
Learn multi-
agent model
Future
motion
Initial conditions
in test data
Training data
Predict by multi-
agent model
Typical techniques:
• RNN [Zheng+16, Le+17, Ivanovic+18]
• Graph NN [Kipf+18, Yeh+19, Monti+20, Graber+20]
• GAN [Chen+18, Hsieh+19]
• Other deep generative models [Zhan+19, Qi+20, Li+20]

20. Conventional data-driven models have three problems
1. fully utilize environmental information (e.g. [Zhan+19, Yeh+19])
2. optimized communication & centralized control (most studies)
3. ignore mechanical constraints of players’ bodies (all studies)
Real-world agents：
1. select players’ importance based on partial observation
2. behave in a decentralized manner
3. reflect physical and biomechanical constraints
Our contributions of this work:
• to construct data-driven models satisfying above requirements
• to validate it by visualizing & generating plausible behaviors
o
x
20

21. Our model components [Fujii+20, arXiv]
Overview
Components (implemented by NN)
① partial observation
② macro-goal
③ local policy
④ physical and biomechanical constraints
a. penalty for inconsistency among pos., vel., & acc.
b. penalty for change in acc. (i.e., smoothness)
④
③
②
①
① binary vector
②[Zhan+19]
(decentralized)
③ VRNN
： learn a binary vector
: used as weak supervision
： variational RNN [Chung+15]
21

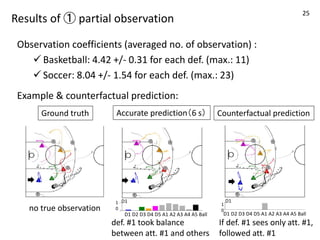
22. Before the detailed method: data and tasks
Datasets
• Soccer: 45 games in Europe leagues (10 Hz, anonymous)
• obtained from https://www.statsperform.com/
• 19968 training, 2235 validation, and 2608 test sequences
• Basketball: 100 games in NBA (25Hz->10 Hz, identified)
• obtained from https://github.com/rajshah4/BasketballData
• 21504 training, 2165 validation, and 2452 test sequences
Prediction task
• who: players’ trajectories in a defensive team [Le+17]
• how long: predict 6-second trajectories from 2-second ones
Model input and output (model: partially observed)
• input： all players pos., vel., and acc., and ball pos. and vel.
• output： each defender’s vel. and acc. (see [Fujii+20])
22

23. Model details and results ③ decentralized local policy
Variational RNN
Root mean squared error (6-s prediction)
[Chung+15, NIPS]
Hierarchical VRNN
with macro goals
Decentralized version
of [Zhan+19, ICLR]
macro-goals
23

24. Model details and results ④ mechanical constraints
We designed the constraint losses (penalties) for optimizing neural networks:
• our model directly predicted vel. & acc. and indirectly did pos. (see [Fujii+20])
1. Difference in distributions (KLD: Kullback–Leibler divergence) between direct and
indirect prediction (e.g. and )
2. Difference between indirect prediction distribution and ground truth
(NLL: Negative Log-Likelihood)
3. Difference between direct prediction distribution and next true acc.
(NLL) based on minimum jerk principle [Flash+85,JNS] for smooth movements
1
2 3
better
24

25. Results of ① partial observation
Observation coefficients (averaged no. of observation) :
✓ Basketball: 4.42 +/- 0.31 for each def. (max.: 11)
✓ Soccer: 8.04 +/- 1.54 for each def. (max.: 23)
Example & counterfactual prediction:
def. #1 took balance
between att. #1 and others
If def. #1 sees only att. #1,
followed att. #1
Counterfactual prediction
D1 D2 D3 D4 D5 A1 A2 A3 A4 A5 Ball
1
0
D1
Accurate prediction（6 s）
Ground truth
no true observation
D1 D2 D3 D4 D5 A1 A2 A3 A4 A5 Ball
1
0
D1
25

26. Conclusion
• Motivation: bridging theory-based and data-driven approaches
to understand multi-agent sports behaviors
• Theory-based data-driven approaches, e.g.,
1. extracting mathematical structures (physical science)
2. modeling the components of multi-agent systems and
generating plausible movements (behavioral science)
Acknowledgements
Yoshinobu Kawahara, Naoya Takeishi, Yuki Inaba, Motokazu Hojo, Kazuya Takeda,
and other colleagues
Grant: KAKENHI 18K18116, 19H04941, 20H04075, JST Presto JPMJPR20CA, etc.
Questions?
（for details, see https://arxiv.org/abs/2102.07545）
26