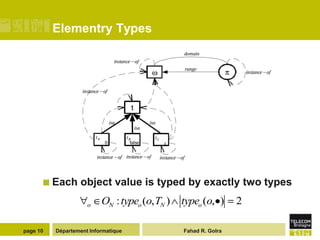
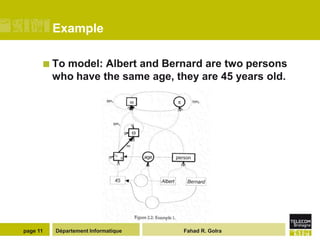
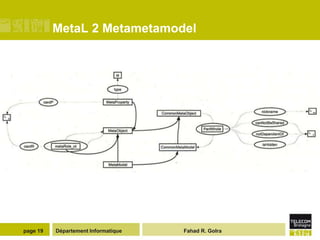
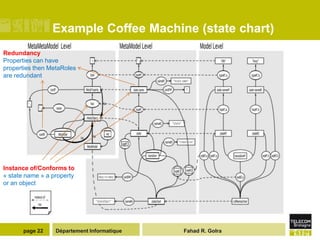
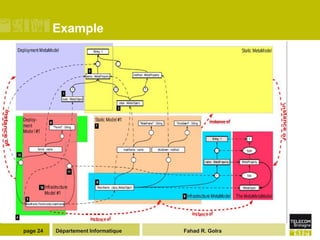
The document describes the MetaL modeling language, which has two layers - MetaL1 and MetaL2. MetaL1 defines a minimal data modeling kernel where all elements are treated as data objects with properties and relationships. MetaL2 provides a formal metamodeling foundation where meta-objects can be extended and refined through multiple inheritance. The language allows for fine-grained sharing and overlapping of meta-models and their elements.

1. MetaL MetaCASE Tools &
Possibilities
Fahad Rafique Golra
19/03/2012 Département Informatique

2. Table of Contents
1. MetaL1
2. MetaL2
3. Examples
4. Benefits
5. Discussion
page 1 Département Informatique Fahad R. Golra

3. MetaL Language
 Two distinct layers
• MetaL 1 (minimal kernel language)
• MetaL 2 (formal foundation)
page 2 Département Informatique Fahad R. Golra

4. MetaL 1 Repository
 Everything in the repository is a dataobject (D: set
of all dataobjects)
 Facets of Dataobject
• Object (O: set of all objects)
• Properties (P: set of all properties)
domain : P  O
range : P  O
« facet of » defines the hidden dataobject
fo : O  P  D
A dataobject can be a property, an object or both
page 3 Département Informatique Fahad R. Golra

5. Properties & Objects
o1, o2 , o3 , op O
op, q P
 op has both a property and an object facet
page 4 Département Informatique Fahad R. Golra

6. Dataobject Types
 The objet type, OT is a subset of O
 The property type, PT is a subset of P
 Instance-type relationship is modeled as
o def
typeo O OT x y typeo x, y
typep P PT p def
x y type p x, y
A property has exactly one property type
 Every object has atleast one object type
page 5 Département Informatique Fahad R. Golra

7. Types
 Thedomain (resp. range) of a property must be an
instance of the domain (resp. range) of its property
type.
o
domain( p)  domain( pt )
and
o
range( p)  range( pt )
page 6 Département Informatique Fahad R. Golra

8. Object values
 Object values are specialized objects that hold
value
val : OB  OS  O  O  O  B  S      
 If x OT then val ( x) T where T denotes any
type N,B, …
 The object value sets are disjoint and are all
included in O.
page 7 Département Informatique Fahad R. Golra

9. Inheritance & Name
 isa relationship isa OT OT
 Objecttypes inherit properties from their
supertypes
typeo (o, t ) t isa* t typeo (o, t )
 Object and property types have unique names
x, y OT : name( x) name( y) x y
p1 , p2 P : name( p1 ) name( p2 )
T
Fam* (domain( p1 )) Fam* (domain( p2 )) p1 p2
page 8 Département Informatique Fahad R. Golra

10. MetaL1 Specification
 Root object type ( ) and property type ( )
( ) is an instance of root object type and
supertype of the elementary types
 For example:
TN OT  ON isa(TN , )
typeo (TN , ) typeo (TN , TN )
val (TN ) 0 name(TN ) int
page 9 Département Informatique Fahad R. Golra

11. Elementry Types
 Each object value is typed by exactly two types
o ON : typeo (o, TN ) typeo (o, ) 2
page 10 Département Informatique Fahad R. Golra

12. Example
 To model: Albert and Bernard are two persons
who have the same age, they are 45 years old.
page 11 Département Informatique Fahad R. Golra

13. Integrity
 If some object o O is deleted
- If p P is a property whose domain( p) o typep ( p, pt ) true for some
pt P and if dr kind ( pt ) then range( p) must also be deleted.
T
- If p P is a property whose range( p) o typep ( p, pt ) true for some
pt P and if rd kind ( p ) then domain( p) must also be deleted.
T t
 If some property p P is deleted
- If pd kind ( pt ) , then domain( p) must be deleted
- If pr kind ( pt ) , then range( p) must be deleted
page 12 Département Informatique Fahad R. Golra

14. MetaL 2 Metametamodel
 CommonMetaObject
- Default supertype of all other metaclasses
 CommonMetaModel
- Default supertype of all constructs denoting metamodels
- Inherits from CommonMetaObject
 MetaObject
- Key metaclass as main concept
- Generalizes MetaRole, MetaProperty, MetaModel
- Has a unique name
page 13 Département Informatique Fahad R. Golra

15. MetaL 2 Metametamodel
 MetaProperty
- Adds slots to metaobjects
- Inherits from MetaObject
- Domain of cardP property which limits the number of concrete
properties
- Cardinality -1 is considered infinite, otherwise ≥ 1
- Must have exactly one cardinality and one type
- Cardinality is the range of exactly one metaproperty
page 14 Département Informatique Fahad R. Golra

16. MetaL 2 Metametamodel
 MetaRole
- Both object type and property type
- As object type, subtype of MetaObject
- As property type, has MetaObject object type as domain and
range
- Domain of cardR property, where cardR denotes one-to-
one(0), one-to-many(1), many-to-one(4), many-to-many(5),
manys-to-manys(10).
- Cardinality is the range of exactly one metarole
page 15 Département Informatique Fahad R. Golra

17. MetaL 2 Metametamodel
 MetaModel
- Aggregate concept defined by a set of metaobjects
- Inherits from CommonMetaModel
- PartWhole metaRole has CommonMetaObject as domain
and CommonMetaModel as range.
- PartWhole is domain of
– nickname:optional, unicity of name inside a metamodel
– canNotBeShared: allows sharing in metamodels
– isNotDependentOn: dependency of object on metamodel
– isHidden: hiding technical details
page 16 Département Informatique Fahad R. Golra

18. Example
 PartWhole
- metametamodel – metaclass
- statechart – state
- coffemachine - IDLE
page 17 Département Informatique Fahad R. Golra

19. MetaL 2 Metametamodel
 Inheritence
- MetaObjects can inherit from other MetaObjects
- Multiple inheritance is allowed
- Cycles are forbidden in the generalization graph
- Inheritance between metamodels is allowed
MM typeo ( , MetaModel)
page 18 Département Informatique Fahad R. Golra

20. MetaL 2 Metametamodel
page 19 Département Informatique Fahad R. Golra

21. MetaL 2 Concrete Layer
 ConcreteObjects
- Instance of metaobject which is instance of MetaObject
- Can belong to several concrete models
- Can not live outside the definition of atleast one concrete
model
 Concrete Property
- Valued slot attached to concrete object
- Can be shared by multiple concrete objects
- As its a metaobject so it can own properties, roles etc
page 20 Département Informatique Fahad R. Golra

22. MetaL 2 Concrete Layer
 Concrete Roles
- Has property and object facets
- Links two objects and can be a domain/range of property
- Respects cardinality
 Concrete Models
- Instance of metamodel which is an instance of MetaModel
- Composed of concrete objects that are instance of
metaobjects in metamodel definition.
page 21 Département Informatique Fahad R. Golra

23. Example Coffee Machine (state chart)
Redundancy
Properties can have
properties then MetaRoles
are redundant
Instance of/Conforms to
« state name » a property
or an object
page 22 Département Informatique Fahad R. Golra

24. General Benefits
- Meta(models) can overlap
- Sharing between (meta)models is fine-grained: (meta)objects,
(meta)models, …
- Multiple instantiation
- Free from instance/type delimitation in modeling layers
- Granularity: meta(models) are meta(objects)
- Metamodel refinement: As metamodels can be extended
further and refined.
page 23 Département Informatique Fahad R. Golra

25. Example
page 24 Département Informatique Fahad R. Golra

26. Points for discussion
• Having shared objects can help transformations, as
some part of the (meta)model remains constant in
transformation
• Maintaining metamodel families by transformations
without referential redundancies
• As other terminal languages can be defined on top
MetaL1, so a complete family of of DSLs can exist
e.g. for Component Oriented Programming.
page 25 Département Informatique Fahad R. Golra

27. References
1. V. Englebert. MetaL1: a formal specification. Technical Report,
University of Namur – PRECISE Research Centre, Belgique,
May 2010.
2. V. Englebert. MetaL2: a formal specification. Technical Report,
University of Namur – PRECISE Research Centre, Belgique,
May 2010.
3. V. Englebert, P. Heymans, “Towards More Extensive
MetaCASE Tools”, In: Proceedings of CAiSE 2007, Springer-
Verlag Berlin Heidelberg, pp 454–468, 2007.
page 26 Département Informatique Fahad R. Golra