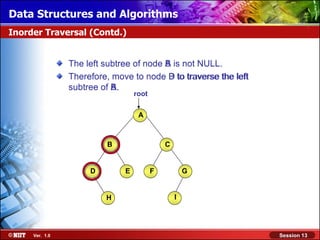
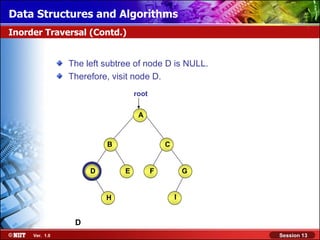
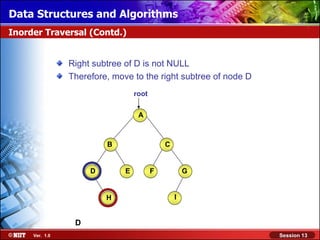
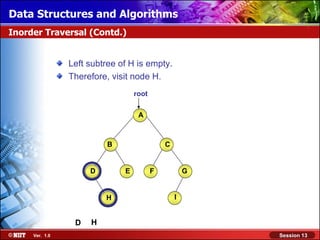
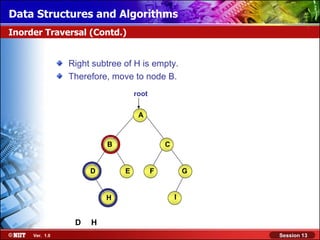
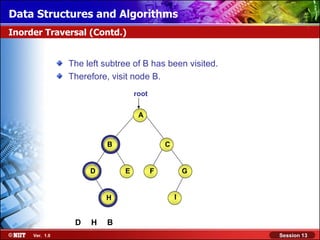
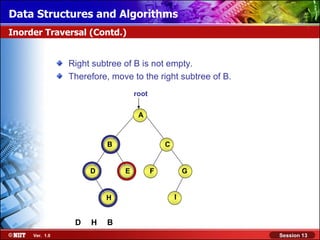
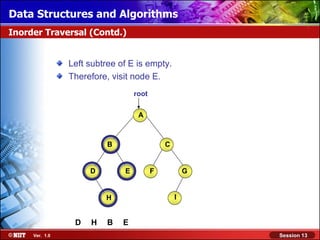
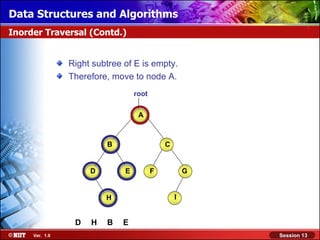
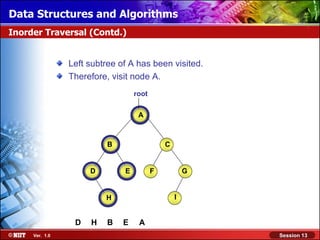
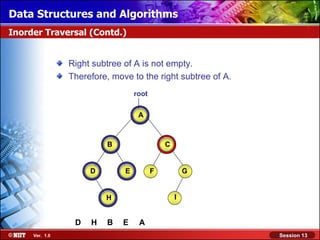
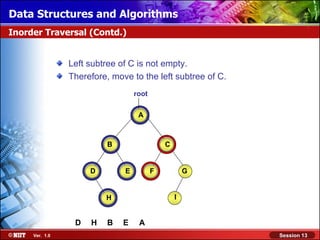
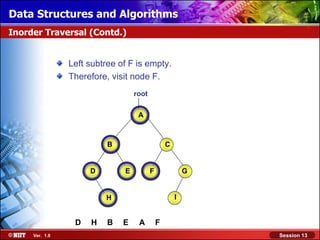
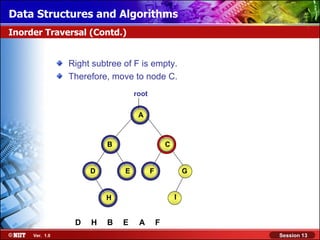
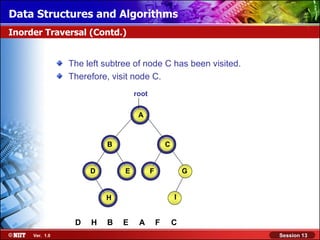
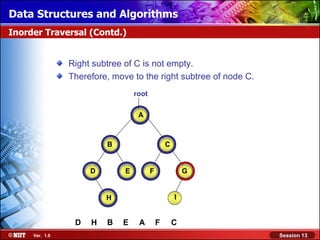
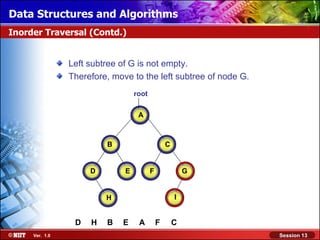
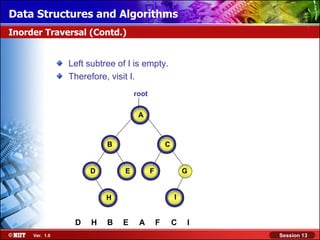
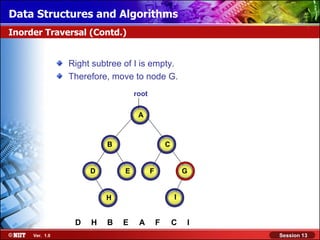
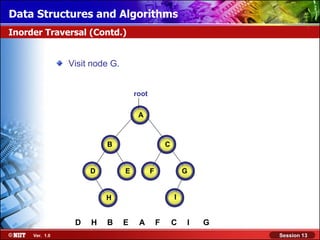
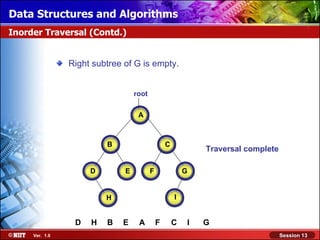
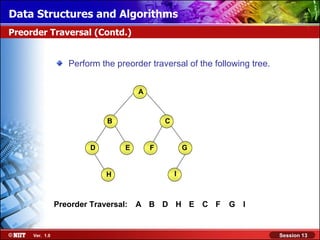
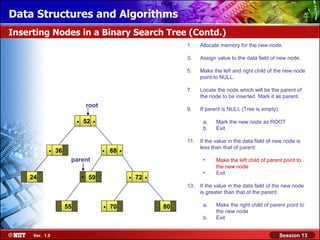
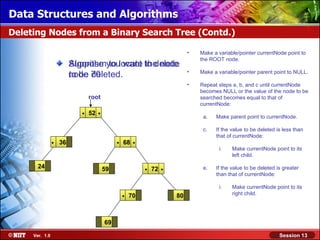
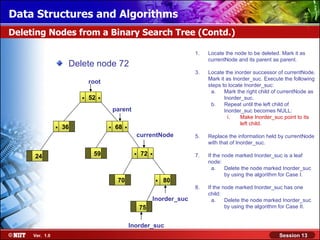
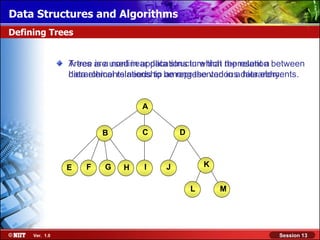
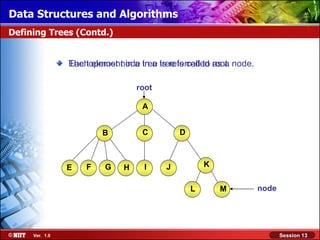
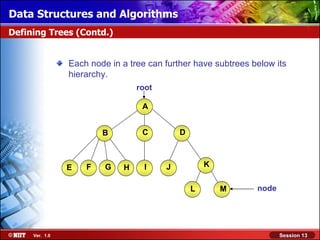
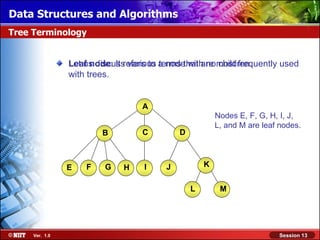
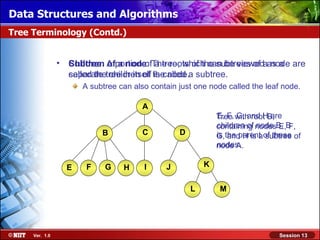
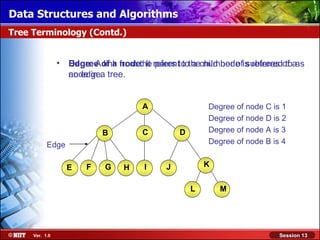
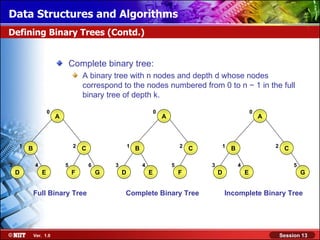
This document discusses binary trees and their terminology. It introduces binary trees as a type of tree where each node has at most two children, namely a left child and a right child. The document then defines various binary tree types and provides examples to illustrate tree terminology such as root, leaf nodes, subtrees, siblings, levels, and depth.

1. Data Structures and Algorithms
Objectives
In this session, you will learn to:
Store data in a tree
Implement a binary tree
Implement a binary search tree
Ver. 1.0 Session 13

2. Data Structures and Algorithms
Storing Data in a Tree
Consider structure where you are required to represent
Directory a scenario
the directory structure of your operating system.
The directory structure contains various folders and files. A
folder may further contain any number of sub folders and
files.
In such a case, it is not possible to represent the structure
linearly because all the items have a hierarchical
relationship among themselves.
In such a case, it would be good if you have a data structure
that enables you to store your data in a nonlinear fashion.
Ver. 1.0 Session 13

3. Data Structures and Algorithms
Defining Trees
A tree are used in applications in which represent a between
Trees is a nonlinear data structure that the relation
hierarchical relationship be represented in adata elements.
data elements needs to among the various hierarchy.
A
B C D
E F G H I J K
L M
Ver. 1.0 Session 13

4. Data Structures and Algorithms
Defining Trees (Contd.)
The topmost node in a is referred to as a
Each element in a tree tree is called root. node.
root
A
B C D
E F G H I J K
L M node
Ver. 1.0 Session 13

5. Data Structures and Algorithms
Defining Trees (Contd.)
Each node in a tree can further have subtrees below its
hierarchy.
root
A
B C D
E F G H I J K
L M node
Ver. 1.0 Session 13

6. Data Structures and Algorithms
Tree Terminology
• Let us discuss various a node with nomost frequently used
Leaf node: It refers to terms that are children.
with trees.
A
Nodes E, F, G, H, I, J,
L, and M are leaf nodes.
B C D
E F G H I J K
L M
Ver. 1.0 Session 13

7. Data Structures and Algorithms
Tree Terminology (Contd.)
• Children A portion ofThe roots of the subtrees of aas a are
Subtree: of a node: a tree, which can be viewed node
called thetree in itself the node.a subtree.
separate children of is called
A subtree can also contain just one node called the leaf node.
A
E, F, G, and H are
Tree with root B,
containing nodesB. B
children of node E, F,
B C D G,the parent of these of
is and H is a subtree
nodes.
node A.
E F G H I J K
L M
Ver. 1.0 Session 13

8. Data Structures and Algorithms
Tree Terminology (Contd.)
• Degree of a from the refers to thechild node is referredof a
Edge: A link node: It parent to a number of subtrees to as
node in a tree.
an edge.
A Degree of node C is 1
Degree of node D is 2
B C D Degree of node A is 3
Edge Degree of node B is 4
E F G H I J K
L M
Ver. 1.0 Session 13

9. Data Structures and Algorithms
Tree Terminology (Contd.)
• Siblings/Brothers: It refers to the children of the same
node.
A Nodes B, C, and D are
siblings of each other.
B C D Nodes E, F, G, and H are
siblings of each other.
E F G H I J K
L M
Ver. 1.0 Session 13

10. Data Structures and Algorithms
Tree Terminology (Contd.)
• Level of node: It refers to to the distance (in number of
Internal a node: It refers any node between the root and a
leaf node.
nodes) of a node from the root. Root always lies at level 0.
As you move down the tree, the level increases by one.
Level 0
A
Nodes B, C, D, and K
are internal nodes. Level 1
B C D
E F G H I J K Level 2
L M Level 3
Ver. 1.0 Session 13

11. Data Structures and Algorithms
Tree Terminology (Contd.)
• Depth of a tree: Refers to the total number of levels in the
tree.
The depth of the following tree is 4.
Level 0
A
Level 1
B C D
E F G H I J K Level 2
L M Level 3
Ver. 1.0 Session 13

12. Data Structures and Algorithms
Just a minute
Consider the following tree and answer the questions that
follow:
a. What is the depth of the tree?
b. Which nodes are children of node B?
c. Which node is the parent of node F?
root
d. What is the level of node E?
e. Which nodes are the siblings of node H?
A
f. Which nodes are the siblings of node D?
g. Which nodes are leaf nodes?
B C
D E F G
H I
Ver. 1.0 Session 13

13. Data Structures and Algorithms
Just a minute
Answer:
a. 4
b. D and E
c. C
d. 2
e. H does not have any siblings
f. The only sibling of D is E
g. F, G, H, and I
Ver. 1.0 Session 13

14. Data Structures and Algorithms
Defining Binary Trees
Binary binary tree:
Strictly tree is a specific type of tree in which each node can
have binary tree in children namely left child and right child.
A at most two which every node, except for the leaf nodes,
There are variousleft and of binary trees:
has non-empty types right children.
Strictly binary tree
Full binary tree
Complete binary tree
Ver. 1.0 Session 13

15. Data Structures and Algorithms
Defining Binary Trees (Contd.)
Full binary tree:
d
A binary tree of depth d that contains exactly 2 – 1
nodes.
A
Depth = 3
Total number of
3
nodes = 2 – 1 = 7
B C
D E F G
Ver. 1.0 Session 13

16. Data Structures and Algorithms
Defining Binary Trees (Contd.)
Complete binary tree:
A binary tree with n nodes and depth d whose nodes
correspond to the nodes numbered from 0 to n − 1 in the full
binary tree of depth k.
0 0 0
A A A
1 B 2 C 1 B 2 C 1 B 2 C
3 4 5 6 3 4 5 3 4 5
D E F G D E F D E G
Full Binary Tree Complete Binary Tree Incomplete Binary Tree
Ver. 1.0 Session 13

17. Data Structures and Algorithms
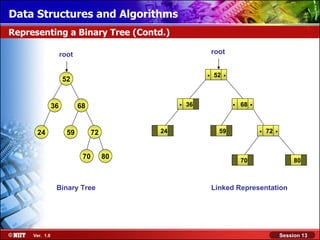
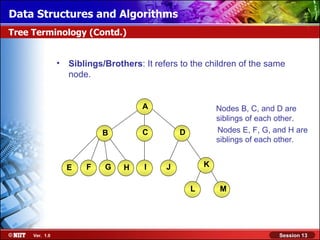
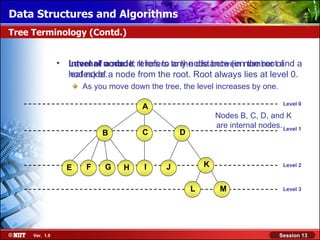
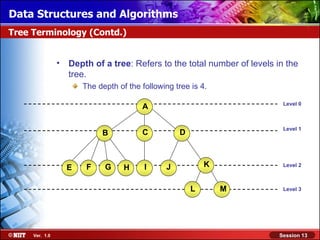
Representing a Binary Tree
Array representation of binary trees: If there are n nodes in a binary
All the nodes are represented as the elements for any node with index
tree, then of an array.
i, where 0 < i < n – 1:
Parent of i is at (i – 1)/2.
A [0] Left child of i is at 2i + 1:
– If 2i + 1 > n – 1, then
B [1] the node does not
0 have a left child.
C [2]
Right child of i is at 2i + 2:
A
– If 2i + 2 > n – 1, then
D [3]
the node does have a
1 2 right child.
E [4]
B C
3 4 5 6 F [5]
D E F G
G [6]
Binary Tree Array Representation
Ver. 1.0 Session 13

18. Data Structures and Algorithms
Representing a Binary Tree (Contd.)
Linked representation of a binary tree:
It uses a linked list to implement a binary tree.
Each node in the linked representation holds the following
information:
– Data
– Reference to the left child
– Reference to the right child
– If a node does not have a left child or a right child or both, the
respective left or right child fields of that node point to NULL.
Data
Node
Ver. 1.0 Session 13

19. Data Structures and Algorithms
Representing a Binary Tree (Contd.)
root root
52
. 52 .
36 68 . 36 . 68 .
24 59 72 24 59 . 72 .
70 80 . 70 80
Binary Tree Linked Representation
Ver. 1.0 Session 13

20. Data Structures and Algorithms
Traversing a Binary Tree
You can implement various operations on a binary tree.
A common operation on a binary tree is traversal.
Traversal refers to the process of visiting all the nodes of a
binary tree once.
There are three ways for traversing a binary tree:
Inorder traversal
Preorder traversal
Postorder traversal
Ver. 1.0 Session 13

21. Data Structures and Algorithms
Inorder Traversal
Steps for traversing a tree in inorder sequence are as
follows:
1. Traverse the left subtree
2. Visit root
3. Traverse the right subtree
• Let us consider an example.
Ver. 1.0 Session 13

22. Data Structures and Algorithms
Inorder Traversal (Contd.)
The left subtree of node B is not NULL.
A
Therefore, move to node D to traverse the left
B
subtree of B.
A.
root
A
B C
D E F G
I
H
Ver. 1.0 Session 13

23. Data Structures and Algorithms
Inorder Traversal (Contd.)
The left subtree of node D is NULL.
Therefore, visit node D.
root
A
B C
D E F G
I
H
D
Ver. 1.0 Session 13

24. Data Structures and Algorithms
Inorder Traversal (Contd.)
Right subtree of D is not NULL
Therefore, move to the right subtree of node D
root
A
B C
D E F G
I
H
D
Ver. 1.0 Session 13

25. Data Structures and Algorithms
Inorder Traversal (Contd.)
Left subtree of H is empty.
Therefore, visit node H.
root
A
B C
D E F G
I
H
D H
Ver. 1.0 Session 13

26. Data Structures and Algorithms
Inorder Traversal (Contd.)
Right subtree of H is empty.
Therefore, move to node B.
root
A
B C
D E F G
I
H
D H
Ver. 1.0 Session 13

27. Data Structures and Algorithms
Inorder Traversal (Contd.)
The left subtree of B has been visited.
Therefore, visit node B.
root
A
B C
D E F G
I
H
D H B
Ver. 1.0 Session 13

28. Data Structures and Algorithms
Inorder Traversal (Contd.)
Right subtree of B is not empty.
Therefore, move to the right subtree of B.
root
A
B C
D E F G
I
H
D H B
Ver. 1.0 Session 13

29. Data Structures and Algorithms
Inorder Traversal (Contd.)
Left subtree of E is empty.
Therefore, visit node E.
root
A
B C
D E F G
I
H
D H B E
Ver. 1.0 Session 13

30. Data Structures and Algorithms
Inorder Traversal (Contd.)
Right subtree of E is empty.
Therefore, move to node A.
root
A
B C
D E F G
I
H
D H B E
Ver. 1.0 Session 13

31. Data Structures and Algorithms
Inorder Traversal (Contd.)
Left subtree of A has been visited.
Therefore, visit node A.
root
A
B C
D E F G
I
H
D H B E A
Ver. 1.0 Session 13

32. Data Structures and Algorithms
Inorder Traversal (Contd.)
Right subtree of A is not empty.
Therefore, move to the right subtree of A.
root
A
B C
D E F G
I
H
D H B E A
Ver. 1.0 Session 13

33. Data Structures and Algorithms
Inorder Traversal (Contd.)
Left subtree of C is not empty.
Therefore, move to the left subtree of C.
root
A
B C
D E F G
I
H
D H B E A
Ver. 1.0 Session 13

34. Data Structures and Algorithms
Inorder Traversal (Contd.)
Left subtree of F is empty.
Therefore, visit node F.
root
A
B C
D E F G
I
H
D H B E A F
Ver. 1.0 Session 13

35. Data Structures and Algorithms
Inorder Traversal (Contd.)
Right subtree of F is empty.
Therefore, move to node C.
root
A
B C
D E F G
I
H
D H B E A F
Ver. 1.0 Session 13

36. Data Structures and Algorithms
Inorder Traversal (Contd.)
The left subtree of node C has been visited.
Therefore, visit node C.
root
A
B C
D E F G
I
H
D H B E A F C
Ver. 1.0 Session 13

37. Data Structures and Algorithms
Inorder Traversal (Contd.)
Right subtree of C is not empty.
Therefore, move to the right subtree of node C.
root
A
B C
D E F G
I
H
D H B E A F C
Ver. 1.0 Session 13

38. Data Structures and Algorithms
Inorder Traversal (Contd.)
Left subtree of G is not empty.
Therefore, move to the left subtree of node G.
root
A
B C
D E F G
I
H
D H B E A F C
Ver. 1.0 Session 13

39. Data Structures and Algorithms
Inorder Traversal (Contd.)
Left subtree of I is empty.
Therefore, visit I.
root
A
B C
D E F G
I
H
D H B E A F C I
Ver. 1.0 Session 13

40. Data Structures and Algorithms
Inorder Traversal (Contd.)
Right subtree of I is empty.
Therefore, move to node G.
root
A
B C
D E F G
I
H
D H B E A F C I
Ver. 1.0 Session 13

41. Data Structures and Algorithms
Inorder Traversal (Contd.)
Visit node G.
root
A
B C
D E F G
I
H
D H B E A F C I G
Ver. 1.0 Session 13

42. Data Structures and Algorithms
Inorder Traversal (Contd.)
Right subtree of G is empty.
root
A
B C
Traversal complete
D E F G
I
H
D H B E A F C I G
Ver. 1.0 Session 13

43. Data Structures and Algorithms
Preorder Traversal
Steps for traversing a tree in preorder sequence are as
follows:
1. Visit root
2. Traverse the left subtree
3. Traverse the right subtree
Ver. 1.0 Session 13

44. Data Structures and Algorithms
Preorder Traversal (Contd.)
Perform the preorder traversal of the following tree.
A
B C
D E F G
I
H
Preorder Traversal: A B D H E C F G I
Ver. 1.0 Session 13

45. Data Structures and Algorithms
Postorder Traversal
Steps for traversing a tree in postorder sequence are as
follows:
1. Traverse the left subtree
2. Traverse the right subtree
3. Visit the root
Ver. 1.0 Session 13

46. Data Structures and Algorithms
Postorder Traversal (Contd.)
Perform the postorder traversal of the following tree.
A
B C
D E F G
I
H
Postorder Traversal: H D E B F I G C A
Ver. 1.0 Session 13

47. Data Structures and Algorithms
Just a minute
In _________ traversal method, root is processed before
traversing the left and right subtrees.
Answer:
Preorder
Ver. 1.0 Session 13

48. Data Structures and Algorithms
Implementing a Binary Search Tree
Consider a scenario. SysCall Ltd. is a cellular phone
company with millions of customers spread across the
world. Each customer is assigned a unique identification
number (id). Individual customer records can be accessed
by referring to the respective id. These ids need to be
stored in a sorted manner in such a way so that you can
perform various transactions, such as retrieval, insertion,
and deletion, easily.
Ver. 1.0 Session 13

49. Data Structures and Algorithms
Implementing a Binary Search Tree (Contd.)
Therefore, you need to implementto store structure the
Which data structure will you use a data the id of that
customers?
provides the advantages of both arrays as well as linked
lists. you implement an array?
Can
– Search operation in an array the advantages of both
A binary search tree combines is fast.
– However, insertion
arrays and linked lists. and deletion in an array is complex in nature.
– In this case, the total number of customer ids to be stored is very
large. Therefore, insertion and deletion will be very time
consuming.
Can you implement a linked list?
Insert and delete operation in a linked is fast.
However, linked lists allow only sequential search.
If you need to access a particular customer id, which is located
near the end of the list, then it would require you to visit all the
preceding nodes, which again can be very time consuming.
Ver. 1.0 Session 13

50. Data Structures and Algorithms
Defining a Binary Search Tree
The following tree example of a binary search tree.
Binary search is an is a binary tree in which every node
satisfies the following conditions:
All values in the left subtree of a node are less than the value
of the node. 52
All values in the right subtree of a node are greater than the
value of the node.
36 68
24 44 59 72
40 55
Ver. 1.0 Session 13

51. Data Structures and Algorithms
Defining a Binary Search Tree (Contd.)
You can implement various operations on a binary search
tree:
Traversal
Search
Insert
Delete
Ver. 1.0 Session 13

52. Data Structures and Algorithms
Searching a Node in a Binary Search Tree
Search operation refers value, process ofto perform the a
To search for a specific to the you need searching for
specified steps: in the tree.
following value
1. Make currentNode point to the root node
2. If currentNode is null:
a. Display “Not Found”
b. Exit
3. Compare the value to be searched with the value of currentNode.
Depending on the result of the comparison, there can be three
possibilities:
a. If the value is equal to the value of currentNode:
i. Display “Found”
ii. Exit
d. If the value is less than the value of currentNode:
i. Make currentNode point to its left child
ii. Go to step 2
g. If the value is greater than the value of currentNode:
i. Make currentNode point to its right child
ii. Go to step 2
Ver. 1.0 Session 13

53. Data Structures and Algorithms
Just a minute
In a binary search tree, all the values in the left subtree of a
node are _______ than the value of the node.
Answer:
smaller
Ver. 1.0 Session 13

54. Data Structures and Algorithms
Inserting Nodes in a Binary Search Tree
Write an algorithmnode in a the position of tree, you firstto be
Before inserting a to locate binary search a new node
inserted check whether the tree.is empty or not.
need to in a binary search tree
If the tree is empty, make the new node as root.
If the tree is not empty, you need to locate the appropriate
position for the new node to be inserted.
This requires you to locate the parent of the new node to be
inserted.
Once the parent is located, the new node is inserted as the
left child or right child of the parent.
To locate the parent of the new node to be inserted, you
need to implement a search operation in the tree.
Ver. 1.0 Session 13

55. Data Structures and Algorithms
Inserting Nodes in a Binary Search Tree (Contd.)
1. Mark the root node as currentNode
Algorithm to locate the 3. Make parent point to NULL
parent of the new node to
5. Repeat steps 4, 5, and 6 until currentNode
be inserted. becomes NULL
7. Make parent point to currentNode
root
9. If the value of the new node is less than that of
. 52 . currentNode:
a. Make currentNode point to its left child
12. If the value of the new node is greater than that
. 36 . 68 . of currentNode:
a. Make currentNode point to its right child
24 59 . 72 .
. 70 80
Ver. 1.0 Session 13

56. Data Structures and Algorithms
Inserting Nodes in a Binary Search Tree (Contd.)
1. Mark the root node as currentNode
Refer to the algorithm to
Locate the position of a new node 55. 3. Make parent point to NULL
locate the parent of the
5. Repeat steps 4, 5, and 6 until currentNode
new node to be inserted. becomes NULL
7. Make parent point to currentNode
root
9. If the value of the new node is less than that of
. 52 . currentNode:
a. Make currentNode point to its left child
11. If the value of the new node is greater than that
. 36 . 68 . of currentNode:
a. Make currentNode point to its right child
24 59 . 72 .
. 70 80
Ver. 1.0 Session 13

57. Data Structures and Algorithms
Inserting Nodes in a Binary Search Tree (Contd.)
• Mark the root node as currentNode
Locate the position of a new node 55. • Make parent point to NULL
• Repeat steps 4, 5, and 6 until currentNode
becomes NULL
• Make parent point to currentNode
root
• If the value of the new node is less than that of
currentNode . 52 . currentNode:
a. Make currentNode point to its left child
11. If the value of the new node is greater than that
. 36 . 68 . of currentNode:
a. Make currentNode point to its right child
24 59 . 72 .
. 70 80
Ver. 1.0 Session 13

58. Data Structures and Algorithms
Inserting Nodes in a Binary Search Tree (Contd.)
• Mark the root node as currentNode
Locate the position of a new node 55. • Make parent point to NULL
• Repeat steps 4, 5, and 6 until currentNode
becomes NULL
• Make parent point to currentNode
root
parent = NULL • If the value of the new node is less than that of
currentNode . 52 . currentNode:
a. Make currentNode point to its left child
11. If the value of the new node is greater than that
. 36 . 68 . of currentNode:
a. Make currentNode point to its right child
24 59 . 72 .
. 70 80
Ver. 1.0 Session 13

59. Data Structures and Algorithms
Inserting Nodes in a Binary Search Tree (Contd.)
• Mark the root node as currentNode
Locate the position of a new node 55. • Make parent point to NULL
• Repeat steps 4, 5, and 6 until currentNode
becomes NULL
• Make parent point to currentNode
root
parent = NULL • If the value of the new node is less than that of
currentNode . 52 . currentNode:
a. Make currentNode point to its left child
11. If the value of the new node is greater than that
. 36 . 68 . of currentNode:
a. Make currentNode point to its right child
24 59 . 72 .
. 70 80
Ver. 1.0 Session 13

60. Data Structures and Algorithms
Inserting Nodes in a Binary Search Tree (Contd.)
• Mark the root node as currentNode
Locate the position of a new node 55. • Make parent point to NULL
• Repeat steps 4, 5, and 6 until currentNode
becomes NULL
• Make parent point to currentNode
root
parent = NULL
parent • If the value of the new node is less than that of
currentNode . 52 . currentNode:
a. Make currentNode point to its left child
11. If the value of the new node is greater than that
. 36 . 68 . of currentNode:
a. Make currentNode point to its right child
24 59 . 72 .
. 70 80
Ver. 1.0 Session 13

61. Data Structures and Algorithms
Inserting Nodes in a Binary Search Tree (Contd.)
• Mark the root node as currentNode
Locate the position of a new node 55. • Make parent point to NULL
• Repeat steps 4, 5, and 6 until currentNode
becomes NULL
55 > 52
• Make parent point to currentNode
root
parent • If the value of the new node is less than that of
currentNode . 52 . currentNode:
a. Make currentNode point to its left child
11. If the value of the new node is greater than that
. 36 . 68 . of currentNode:
a. Make currentNode point to its right child
24 59 . 72 .
. 70 80
Ver. 1.0 Session 13

62. Data Structures and Algorithms
Inserting Nodes in a Binary Search Tree (Contd.)
1. Mark the root node as currentNode
Locate the position of a new node 55. 3. Make parent point to NULL
5. Repeat steps 4, 5, and 6 until currentNode
becomes NULL
55 > 52
7. Make parent point to currentNode
root
parent 9. If the value of the new node is less than that of
currentNode . 52 . currentNode:
a. Make currentNode point to its left child
11. If the value of the new node is greater than that
. 36 . 68 . of currentNode:
a. Make currentNode point to its right child
24 59 . 72 .
. 70 80
Ver. 1.0 Session 13

63. Data Structures and Algorithms
Inserting Nodes in a Binary Search Tree (Contd.)
1. Mark the root node as currentNode
Locate the position of a new node 55. 3. Make parent point to NULL
5. Repeat steps 4, 5, and 6 until currentNode
becomes NULL
55 > 52
7. Make parent point to currentNode
root
parent 9. If the value of the new node is less than that of
currentNode . 52 . currentNode:
a. Make currentNode point to its left child
currentNode
11. If the value of the new node is greater than that
. 36 . 68 . of currentNode:
a. Make currentNode point to its right child
24 59 . 72 .
. 70 80
Ver. 1.0 Session 13

64. Data Structures and Algorithms
Inserting Nodes in a Binary Search Tree (Contd.)
• Mark the root node as currentNode
Locate the position of a new node 55. • Make parent point to NULL
• Repeat steps 4, 5, and 6 until currentNode
becomes NULL
• Make parent point to currentNode
root
parent • If the value of the new node is less than that of
. 52 . currentNode:
a. Make currentNode point to its left child
currentNode
11. If the value of the new node is greater than that
. 36 . 68 . of currentNode:
a. Make currentNode point to its right child
24 59 . 72 .
. 70 80
Ver. 1.0 Session 13

65. Data Structures and Algorithms
Inserting Nodes in a Binary Search Tree (Contd.)
• Mark the root node as currentNode
Locate the position of a new node 55. • Make parent point to NULL
• Repeat steps 4, 5, and 6 until currentNode
becomes NULL
• Make parent point to currentNode
root
parent • If the value of the new node is less than that of
. 52 . currentNode:
a. Make currentNode point to its left child
parent currentNode
11. If the value of the new node is greater than that
. 36 . 68 . of currentNode:
a. Make currentNode point to its right child
24 59 . 72 .
. 70 80
Ver. 1.0 Session 13

66. Data Structures and Algorithms
Inserting Nodes in a Binary Search Tree (Contd.)
• Mark the root node as currentNode
Locate the position of a new node 55. • Make parent point to NULL
• Repeat steps 4, 5, and 6 until currentNode
becomes NULL
55 < 68
• Make parent point to currentNode
root
• If the value of the new node is less than that of
. 52 . currentNode:
a. Make currentNode point to its left child
parent currentNode
11. If the value of the new node is greater than that
. 36 . 68 . of currentNode:
a. Make currentNode point to its right child
24 59 . 72 .
. 70 80
Ver. 1.0 Session 13

67. Data Structures and Algorithms
Inserting Nodes in a Binary Search Tree (Contd.)
1. Mark the root node as currentNode
Locate the position of a new node 55. 3. Make parent point to NULL
5. Repeat steps 4, 5, and 6 until currentNode
becomes NULL
55 < 68
7. Make parent point to currentNode
root
9. If the value of the new node is less than that of
. 52 . currentNode:
a. Make currentNode point to its left child
parent currentNode
11. If the value of the new node is greater than that
. 36 . 68 . of currentNode:
a. Make currentNode point to its right child
24 59 . 72 .
currentNode
. 70 80
Ver. 1.0 Session 13

68. Data Structures and Algorithms
Inserting Nodes in a Binary Search Tree (Contd.)
• Mark the root node as currentNode
Locate the position of a new node 55. • Make parent point to NULL
• Repeat steps 4, 5, and 6 until currentNode
becomes NULL
• Make parent point to currentNode
root
• If the value of the new node is less than that of
. 52 . currentNode:
a. Make currentNode point to its left child
parent
11. If the value of the new node is greater than that
. 36 . 68 . of currentNode:
a. Make currentNode point to its right child
24 59 . 72 .
currentNode
. 70 80
Ver. 1.0 Session 13

69. Data Structures and Algorithms
Inserting Nodes in a Binary Search Tree (Contd.)
• Mark the root node as currentNode
Locate the position of a new node 55. • Make parent point to NULL
• Repeat steps 4, 5, and 6 until currentNode
becomes NULL
• Make parent point to currentNode
root
• If the value of the new node is less than that of
. 52 . currentNode:
a. Make currentNode point to its left child
parent
11. If the value of the new node is greater than that
. 36 . 68 . of currentNode:
parent a. Make currentNode point to its right child
24 59 . 72 .
currentNode
. 70 80
Ver. 1.0 Session 13

70. Data Structures and Algorithms
Inserting Nodes in a Binary Search Tree (Contd.)
• Mark the root node as currentNode
Locate the position of a new node 55. • Make parent point to NULL
• Repeat steps 4, 5, and 6 until currentNode
becomes NULL
55 < 59
• Make parent point to currentNode
root
• If the value of the new node is less than that of
. 52 . currentNode:
a. Make currentNode point to its left child
11. If the value of the new node is greater than that
. 36 . 68 . of currentNode:
parent a. Make currentNode point to its right child
24 59 . 72 .
currentNode
. 70 80
Ver. 1.0 Session 13

71. Data Structures and Algorithms
Inserting Nodes in a Binary Search Tree (Contd.)
1. Mark the root node as currentNode
Locate the position of a new node 55. 3. Make parent point to NULL
5. Repeat steps 4, 5, and 6 until currentNode
becomes NULL
55 < 59
7. Make parent point to currentNode
root
9. If the value of the new node is less than that of
. 52 . currentNode:
a. Make currentNode point to its left child
11. If the value of the new node is greater than that
. 36 . 68 . of currentNode:
parent a. Make currentNode point to its right child
24 59 . 72 .
currentNode
currentNode = NULL
. 70 80
Ver. 1.0 Session 13

72. Data Structures and Algorithms
Inserting Nodes in a Binary Search Tree (Contd.)
• Mark the root node as currentNode
Locate the position of a new node 55. • Make parent point to NULL
• Repeat steps 4, 5, and 6 until currentNode
becomes NULL
• Make parent point to currentNode
root
• If the value of the new node is less than that of
. 52 . currentNode:
a. Make currentNode point to its left child
11. If the value of the new node is greater than that
. 36 . 68 . of currentNode:
parent a. Make currentNode point to its right child
24 59 . 72 .
currentNode = NULL
. 70 80
Ver. 1.0 Session 13

73. Data Structures and Algorithms
Inserting Nodes in a Binary Search Tree (Contd.)
1. Mark the root node as currentNode
Once the parent of the new 3. Make parent point to NULL
node is located, you can
5. Repeat steps 4, 5, and 6 until currentNode
insert the node as the child becomes NULL
of its parent. 7. Make parent point to currentNode
root
9. If the value of the new node is less than that of
. 52 . currentNode:
a. Make currentNode point to its left child
11. If the value of the new node is greater than that
. 36 . 68 . of currentNode:
parent a. Make currentNode point to its right child
24 59 . 72 .
currentNode = NULL
. 70 80
Ver. 1.0 Session 13

74. Data Structures and Algorithms
Inserting Nodes in a Binary Search Tree (Contd.)
Write an algorithm to insert a node in a binary search tree.
Ver. 1.0 Session 13

75. Data Structures and Algorithms
Inserting Nodes in a Binary Search Tree (Contd.)
1. Allocate memory for the new node.
3. Assign value to the data field of new node.
Insert 55
Algorithm to insert a node
5. Make the left and right child of the new node
in a binary search tree. point to NULL.
7. Locate the node which will be the parent of
the node to be inserted. Mark it as parent.
root
9. If parent is NULL (Tree is empty):
. 52 . a. Mark the new node as ROOT
b. Exit
11. If the value in the data field of new node is
. 36 . 68 . less than that of parent:
a. Make the left child of parent point to
the new node
24 59 . 72 . b. Exit
13. If the value in the data field of the new node
is greater than that of the parent:
. 70 80 a. Make the right child of parent point to
the new node
b. Exit
Ver. 1.0 Session 13

76. Data Structures and Algorithms
Inserting Nodes in a Binary Search Tree (Contd.)
• Allocate memory for the new node.
• Assign value to the data field of new node.
• Make the left and right child of the new node
point to NULL.
• Locate the node which will be the parent of
the node to be inserted. Mark it as parent.
root
• If parent is NULL (Tree is empty):
. 52 . a. Mark the new node as ROOT
b. Exit
11. If the value in the data field of new node is
. 36 . 68 . less than that of parent:
a. Make the left child of parent point to
the new node
24 59 . 72 . b. Exit
13. If the value in the data field of the new node
is greater than that of the parent:
. 70 80 a. Make the right child of parent point to
the new node
b. Exit
Ver. 1.0 Session 13

77. Data Structures and Algorithms
Inserting Nodes in a Binary Search Tree (Contd.)
• Allocate memory for the new node.
• Assign value to the data field of new node.
• Make the left and right child of the new node
point to NULL.
• Locate the node which will be the parent of
the node to be inserted. Mark it as parent.
root
• If parent is NULL (Tree is empty):
. 52 . a. Mark the new node as ROOT
b. Exit
11. If the value in the data field of new node is
. 36 . 68 . less than that of parent:
a. Make the left child of parent point to
the new node
24 59 . 72 . b. Exit
13. If the value in the data field of the new node
is greater than that of the parent:
55 . 70 80 a. Make the right child of parent point to
the new node
b. Exit
Ver. 1.0 Session 13

78. Data Structures and Algorithms
Inserting Nodes in a Binary Search Tree (Contd.)
• Allocate memory for the new node.
• Assign value to the data field of new node.
• Make the left and right child of the new node
point to NULL.
• Locate the node which will be the parent of
the node to be inserted. Mark it as parent.
root
• If parent is NULL (Tree is empty):
. 52 . a. Mark the new node as ROOT
b. Exit
11. If the value in the data field of new node is
. 36 . 68 . less than that of parent:
a. Make the left child of parent point to
the new node
24 59 . 72 . b. Exit
13. If the value in the data field of the new node
is greater than that of the parent:
55 . 70 80 a. Make the right child of parent point to
the new node
b. Exit
Ver. 1.0 Session 13

79. Data Structures and Algorithms
Inserting Nodes in a Binary Search Tree (Contd.)
• Allocate memory for the new node.
• Assign value to the data field of new node.
• Make the left and right child of the new node
point to NULL.
• Locate the node which will be the parent of
the node to be inserted. Mark it as parent.
root
• If parent is NULL (Tree is empty):
. 52 . a. Mark the new node as ROOT
b. Exit
11. If the value in the data field of new node is
. 36 . 68 . less than that of parent:
parent a. Make the left child of parent point to
the new node
24 59 . 72 . b. Exit
13. If the value in the data field of the new node
is greater than that of the parent:
55 . 70 80 a. Make the right child of parent point to
the new node
b. Exit
Ver. 1.0 Session 13

80. Data Structures and Algorithms
Inserting Nodes in a Binary Search Tree (Contd.)
• Allocate memory for the new node.
• Assign value to the data field of new node.
• Make the left and right child of the new node
point to NULL.
• Locate the node which will be the parent of
the node to be inserted. Mark it as parent.
root
• If parent is NULL (Tree is empty):
. 52 . a. Mark the new node as ROOT
b. Exit
11. If the value in the data field of new node is
. 36 . 68 . less than that of parent:
parent a. Make the left child of parent point to
the new node
24 59 . 72 . b. Exit
13. If the value in the data field of the new node
is greater than that of the parent:
55 . 70 80 a. Make the right child of parent point to
the new node
b. Exit
Ver. 1.0 Session 13

81. Data Structures and Algorithms
Inserting Nodes in a Binary Search Tree (Contd.)
1. Allocate memory for the new node.
3. Assign value to the data field of new node.
5. Make the left and right child of the new node
point to NULL.
7. Locate the node which will be the parent of
the node to be inserted. Mark it as parent.
root
9. If parent is NULL (Tree is empty):
. 52 . a. Mark the new node as ROOT
b. Exit
11. If the value in the data field of new node is
. 36 . 68 . less than that of parent:
parent a. Make the left child of parent point to
the new node
24 59 . 72 . b. Exit
13. If the value in the data field of the new node
is greater than that of the parent:
55 . 70 80 a. Make the right child of parent point to
the new node
b. Exit
Ver. 1.0 Session 13

82. Data Structures and Algorithms
Inserting Nodes in a Binary Search Tree (Contd.)
1. Allocate memory for the new node.
3. Assign value to the data field of new node.
5. Make the left and right child of the new node
point to NULL.
7. Locate the node which will be the parent of
the node to be inserted. Mark it as parent.
root
9. If parent is NULL (Tree is empty):
. 52 . a. Mark the new node as ROOT
b. Exit
11. If the value in the data field of new node is
. 36 . 68 . less than that of parent:
parent • Make the left child of parent point to
the new node
24 . 59 . 72 . • Exit
13. If the value in the data field of the new node
is greater than that of the parent:
55 . 70 80 a. Make the right child of parent point to
the new node
b. Exit
Ver. 1.0 Session 13

83. Data Structures and Algorithms
Inserting Nodes in a Binary Search Tree (Contd.)
1. Allocate memory for the new node.
3. Assign value to the data field of new node.
5. Make the left and right child of the new node
point to NULL.
7. Locate the node which will be the parent of
the node to be inserted. Mark it as parent.
root
9. If parent is NULL (Tree is empty):
. 52 . a. Mark the new node as ROOT
b. Exit
11. If the value in the data field of new node is
. 36 . 68 . less than that of parent:
parent • Make the left child of parent point to
the new node
24 59 . 72 . • Exit
13. If the value in the data field of the new node
is greater than that of the parent:
55 . 70 80 a. Make the right child of parent point to
the new node
b. Exit
Insert operation complete
Ver. 1.0 Session 13

84. Data Structures and Algorithms
Deleting Nodes from a Binary Search Tree
Write an algorithm to locate the position refers node to
Delete operation in a binary search tree of the to the
process of deleting the specified node from the tree.
deleted from a binary search tree.
Before implementing a delete operation, you first need to
locate the position of the node to be deleted and its parent.
To locate the position of the node to be deleted and its
parent, you need to implement a search operation.
Ver. 1.0 Session 13

85. Data Structures and Algorithms
Deleting Nodes from a Binary Search Tree (Contd.)
• Make a variable/pointer currentNode point to
the ROOT node.
Suppose youlocate to delete
Algorithm to want the node
• Make a variable/pointer parent point to NULL.
node 70
to be deleted.
• Repeat steps a, b, and c until currentNode
becomes NULL or the value of the node to be
root searched becomes equal to that of
currentNode:
. 52 . a. Make parent point to currentNode.
c. If the value to be deleted is less than
that of currentNode:
. 36 . 68 .
i. Make currentNode point to its
left child.
24 59 . 72 . e. If the value to be deleted is greater
than that of currentNode:
i. Make currentNode point to its
. 70 80 right child.
69
Ver. 1.0 Session 13

86. Data Structures and Algorithms
Deleting Nodes from a Binary Search Tree (Contd.)
• Make a variable/pointer currentNode point to
the ROOT node.
Suppose you want to delete
• Make a variable/pointer parent point to NULL.
node 70
• Repeat steps a, b, and c until currentNode
becomes NULL or the value of the node to be
root searched becomes equal to that of
currentNode:
currentNode . 52 . a. Make parent point to currentNode.
c. If the value to be deleted is less than
that of currentNode:
. 36 . 68 .
i. Make currentNode point to its
left child.
24 59 . 72 . e. If the value to be deleted is greater
than that of currentNode:
i. Make currentNode point to its
. 70 80 right child.
69
Ver. 1.0 Session 13

87. Data Structures and Algorithms
Deleting Nodes from a Binary Search Tree (Contd.)
• Make a variable/pointer currentNode point to
the ROOT node.
Suppose you want to delete
• Make a variable/pointer parent point to NULL.
node 70
• Repeat steps a, b, and c until currentNode
becomes NULL or the value of the node to be
root searched becomes equal to that of
currentNode:
currentNode . 52 . a. Make parent point to currentNode.
parent = NULL
c. If the value to be deleted is less than
that of currentNode:
. 36 . 68 .
i. Make currentNode point to its
left child.
24 59 . 72 . e. If the value to be deleted is greater
than that of currentNode:
i. Make currentNode point to its
. 70 80 right child.
69
Ver. 1.0 Session 13

88. Data Structures and Algorithms
Deleting Nodes from a Binary Search Tree (Contd.)
• Make a variable/pointer currentNode point to
the ROOT node.
Suppose you want to delete
• Make a variable/pointer parent point to NULL.
node 70
• Repeat steps a, b, and c until currentNode
becomes NULL or the value of the node to be
root searched becomes equal to that of
currentNode:
currentNode . 52 . a. Make parent point to currentNode.
parent = NULL
c. If the value to be deleted is less than
that of currentNode:
. 36 . 68 .
i. Make currentNode point to its
left child.
24 59 . 72 . e. If the value to be deleted is greater
than that of currentNode:
i. Make currentNode point to its
. 70 80 right child.
69
Ver. 1.0 Session 13

89. Data Structures and Algorithms
Deleting Nodes from a Binary Search Tree (Contd.)
• Make a variable/pointer currentNode point to
the ROOT node.
Suppose you want to delete
• Make a variable/pointer parent point to NULL.
node 70
• Repeat steps a, b, and c until currentNode
becomes NULL or the value of the node to be
root searched becomes equal to that of
currentNode:
currentNode . 52 . parent
• Make parent point to currentNode.
parent = NULL
• If the value to be deleted is less than
that of currentNode:
. 36 . 68 .
i. Make currentNode point to its
left child.
24 59 . 72 . e. If the value to be deleted is greater
than that of currentNode:
i. Make currentNode point to its
. 70 80 right child.
69
Ver. 1.0 Session 13

90. Data Structures and Algorithms
Deleting Nodes from a Binary Search Tree (Contd.)
• Make a variable/pointer currentNode point to
the ROOT node.
Suppose you want to delete
• Make a variable/pointer parent point to NULL.
node 70
• Repeat steps a, b, and c until currentNode
becomes NULL or the value of the node to be
root searched becomes equal to that of
currentNode:
currentNode . 52 . parent
• Make parent point to currentNode.
• If the value to be deleted is less than
that of currentNode:
. 36 . 68 . 70 > 52
i. Make currentNode point to its
left child.
24 59 . 72 . e. If the value to be deleted is greater
than that of currentNode:
i. Make currentNode point to its
. 70 80 right child.
69
Ver. 1.0 Session 13

91. Data Structures and Algorithms
Deleting Nodes from a Binary Search Tree (Contd.)
• Make a variable/pointer currentNode point to
the ROOT node.
Suppose you want to delete
• Make a variable/pointer parent point to NULL.
node 70
• Repeat steps a, b, and c until currentNode
becomes NULL or the value of the node to be
root searched becomes equal to that of
currentNode:
currentNode . 52 . parent
a. Make parent point to currentNode.
c. If the value to be deleted is less than
that of currentNode:
. 36 . 68 . 70 > 52
i. Make currentNode point to its
left child.
24 59 . 72 . e. If the value to be deleted is greater
than that of currentNode:
i. Make currentNode point to its
. 70 80 right child.
69
Ver. 1.0 Session 13

92. Data Structures and Algorithms
Deleting Nodes from a Binary Search Tree (Contd.)
• Make a variable/pointer currentNode point to
the ROOT node.
Suppose you want to delete
• Make a variable/pointer parent point to NULL.
node 70
• Repeat steps a, b, and c until currentNode
becomes NULL or the value of the node to be
root searched becomes equal to that of
currentNode:
currentNode . 52 . parent
a. Make parent point to currentNode.
currentNode
c. If the value to be deleted is less than
that of currentNode:
. 36 . 68 . 70 > 52
i. Make currentNode point to its
left child.
24 59 . 72 . e. If the value to be deleted is greater
than that of currentNode:
i. Make currentNode point to its
. 70 80 right child.
69
Ver. 1.0 Session 13

93. Data Structures and Algorithms
Deleting Nodes from a Binary Search Tree (Contd.)
• Make a variable/pointer currentNode point to
the ROOT node.
Suppose you want to delete
• Make a variable/pointer parent point to NULL.
node 70
• Repeat steps a, b, and c until currentNode
becomes NULL or the value of the node to be
root searched becomes equal to that of
currentNode:
. 52 . parent
a. Make parent point to currentNode.
currentNode
c. If the value to be deleted is less than
that of currentNode:
. 36 . 68 .
i. Make currentNode point to its
left child.
24 59 . 72 . e. If the value to be deleted is greater
than that of currentNode:
i. Make currentNode point to its
. 70 80 right child.
69
Ver. 1.0 Session 13

94. Data Structures and Algorithms
Deleting Nodes from a Binary Search Tree (Contd.)
• Make a variable/pointer currentNode point to
the ROOT node.
Suppose you want to delete
• Make a variable/pointer parent point to NULL.
node 70
• Repeat steps a, b, and c until currentNode
becomes NULL or the value of the node to be
root searched becomes equal to that of
currentNode:
. 52 . parent
• Make parent point to currentNode.
currentNode
• If the value to be deleted is less than
that of currentNode:
. 36 parent . 68 .
i. Make currentNode point to its
left child.
24 59 . 72 . e. If the value to be deleted is greater
than that of currentNode:
i. Make currentNode point to its
. 70 80 right child.
69
Ver. 1.0 Session 13

95. Data Structures and Algorithms
Deleting Nodes from a Binary Search Tree (Contd.)
• Make a variable/pointer currentNode point to
the ROOT node.
Suppose you want to delete
• Make a variable/pointer parent point to NULL.
node 70
• Repeat steps a, b, and c until currentNode
becomes NULL or the value of the node to be
root searched becomes equal to that of
70 > 68 currentNode:
. 52 . • Make parent point to currentNode.
currentNode
• If the value to be deleted is less than
that of currentNode:
. 36 parent . 68 .
i. Make currentNode point to its
left child.
24 59 . 72 . e. If the value to be deleted is greater
than that of currentNode:
i. Make currentNode point to its
. 70 80 right child.
69
Ver. 1.0 Session 13

96. Data Structures and Algorithms
Deleting Nodes from a Binary Search Tree (Contd.)
• Make a variable/pointer currentNode point to
the ROOT node.
Suppose you want to delete
• Make a variable/pointer parent point to NULL.
node 70
• Repeat steps a, b, and c until currentNode
becomes NULL or the value of the node to be
root searched becomes equal to that of
70 > 68 currentNode:
. 52 . a. Make parent point to currentNode.
currentNode
c. If the value to be deleted is less than
that of currentNode:
. 36 parent . 68 .
• Make currentNode point to its
left child.
24 59 . 72 . e. If the value to be deleted is greater
than that of currentNode:
i. Make currentNode point to its
. 70 80 right child.
69
Ver. 1.0 Session 13

97. Data Structures and Algorithms
Deleting Nodes from a Binary Search Tree (Contd.)
• Make a variable/pointer currentNode point to
the ROOT node.
Suppose you want to delete
• Make a variable/pointer parent point to NULL.
node 70
• Repeat steps a, b, and c until currentNode
becomes NULL or the value of the node to be
root searched becomes equal to that of
70 > 68 currentNode:
. 52 . a. Make parent point to currentNode.
currentNode
c. If the value to be deleted is less than
that of currentNode:
. 36 parent . 68 .
currentNode i. Make currentNode point to its
left child.
24 59 . 72 . e. If the value to be deleted is greater
than that of currentNode:
i. Make currentNode point to its
. 70 80 right child.
69
Ver. 1.0 Session 13

98. Data Structures and Algorithms
Deleting Nodes from a Binary Search Tree (Contd.)
• Make a variable/pointer currentNode point to
the ROOT node.
Suppose you want to delete
• Make a variable/pointer parent point to NULL.
node 70
• Repeat steps a, b, and c until currentNode
becomes NULL or the value of the node to be
root searched becomes equal to that of
currentNode:
. 52 . a. Make parent point to currentNode.
c. If the value to be deleted is less than
that of currentNode:
. 36 parent . 68 .
currentNode i. Make currentNode point to its
left child.
24 59 . 72 . e. If the value to be deleted is greater
than that of currentNode:
i. Make currentNode point to its
. 70 80 right child.
69
Ver. 1.0 Session 13

99. Data Structures and Algorithms
Deleting Nodes from a Binary Search Tree (Contd.)
• Make a variable/pointer currentNode point to
the ROOT node.
Suppose you want to delete
• Make a variable/pointer parent point to NULL.
node 70
• Repeat steps a, b, and c until currentNode
becomes NULL or the value of the node to be
root searched becomes equal to that of
currentNode:
. 52 . • Make parent point to currentNode.
• If the value to be deleted is less than
that of currentNode:
. 36 parent . 68 .
currentNode i. Make currentNode point to its
left child.
24 59 . 72 . e. If the value to be deleted is greater
than that of currentNode:
parent i. Make currentNode point to its
. 70 80 right child.
69
Ver. 1.0 Session 13

100. Data Structures and Algorithms
Deleting Nodes from a Binary Search Tree (Contd.)
• Make a variable/pointer currentNode point to
the ROOT node.
Suppose you want to delete
• Make a variable/pointer parent point to NULL.
node 70
• Repeat steps a, b, and c until currentNode
becomes NULL or the value of the node to be
root searched becomes equal to that of
currentNode:
. 52 .
70 < 72 • Make parent point to currentNode.
• If the value to be deleted is less than
that of currentNode:
. 36 . 68 .
currentNode i. Make currentNode point to its
left child.
24 59 . 72 . e. If the value to be deleted is greater
than that of currentNode:
parent i. Make currentNode point to its
. 70 80 right child.
69
Ver. 1.0 Session 13

101. Data Structures and Algorithms
Deleting Nodes from a Binary Search Tree (Contd.)
• Make a variable/pointer currentNode point to
the ROOT node.
Suppose you want to delete
• Make a variable/pointer parent point to NULL.
node 70
• Repeat steps a, b, and c until currentNode
becomes NULL or the value of the node to be
root searched becomes equal to that of
currentNode:
. 52 . 70 < 72 a. Make parent point to currentNode.
c. If the value to be deleted is less than
that of currentNode:
. 36 . 68 .
currentNode i. Make currentNode point to its
left child.
24 59 . 72 . e. If the value to be deleted is greater
than that of currentNode:
parent i. Make currentNode point to its
. 70 80 right child.
currentNode
69
Ver. 1.0 Session 13

102. Data Structures and Algorithms
Deleting Nodes from a Binary Search Tree (Contd.)
• Make a variable/pointer currentNode point to
the ROOT node.
Suppose you want to delete
• Make a variable/pointer parent point to NULL.
node 70
• Repeat steps a, b, and c until currentNode
becomes NULL or the value of the node to be
root searched becomes equal to that of
currentNode:
. 52 . a. Make parent point to currentNode.
c. If the value to be deleted is less than
that of currentNode:
. 36 . 68 .
i. Make currentNode point to its
left child.
24 59 . 72 . e. If the value to be deleted is greater
than that of currentNode:
parent i. Make currentNode point to its
Nodes located . 70 80 right child.
currentNode
69
Ver. 1.0 Session 13

103. Data Structures and Algorithms
Deleting Nodes from a Binary Search Tree (Contd.)
Once the nodes are located, there can be three cases:
Case I: Node to be deleted is the leaf node
Case II: Node to be deleted has one child (left or right)
Case III: Node to be deleted has two children
Ver. 1.0 Session 13

104. Data Structures and Algorithms
Deleting Nodes from a Binary Search Tree (Contd.)
Write an algorithm to delete a leaf node from a binary
search tree.
Ver. 1.0 Session 13

105. Data Structures and Algorithms
Deleting Nodes from a Binary Search Tree (Contd.)
• Locate the node to be deleted. Mark it as
Algorithm to delete a leaf
Delete node 69 currentNode and its parent as parent.
node from the binary tree. • If currentNode is the root node: // If parent is
// NULL
a. Make ROOT point to NULL.
. 52 . b. Go to step 5.
6. If currentNode is left child of parent:
. 36 . 68 . a. Make left child field of parent point to
NULL.
b. Go to step 5.
24 59 . 72 . 8. If currentNode is right child of parent:
a. Make right child field of parent point to
NULL.
b. Go to step 5.
. 70 80
10. Release the memory for currentNode.
69
Ver. 1.0 Session 13

106. Data Structures and Algorithms
Deleting Nodes from a Binary Search Tree (Contd.)
• Locate the node to be deleted. Mark it as
Delete node 69 currentNode and its parent as parent.
• If currentNode is the root node: // If parent is
// NULL
a. Make ROOT point to NULL.
. 52 . b. Go to step 5.
6. If currentNode is left child of parent:
. 36 . 68 . a. Make left child field of parent point to
NULL.
b. Go to step 5.
24 59 . 72 . 8. If currentNode is right child of parent:
a. Make right child field of parent point to
NULL.
b. Go to step 5.
. 70 80
10. Release the memory for currentNode.
parent
69
currentNode
Ver. 1.0 Session 13

107. Data Structures and Algorithms
Deleting Nodes from a Binary Search Tree (Contd.)
• Locate the node to be deleted. Mark it as
Delete node 69 currentNode and its parent as parent.
• If currentNode is the root node: // If parent is
// NULL
a. Make ROOT point to NULL.
. 52 . b. Go to step 5.
6. If currentNode is left child of parent:
. 36 . 68 . a. Make left child field of parent point to
NULL.
b. Go to step 5.
24 59 . 72 . 8. If currentNode is right child of parent:
a. Make right child field of parent point to
NULL.
b. Go to step 5.
. 70 80
10. Release the memory for currentNode.
parent
69
currentNode
Ver. 1.0 Session 13

108. Data Structures and Algorithms
Deleting Nodes from a Binary Search Tree (Contd.)
• Locate the node to be deleted. Mark it as
Delete node 69 currentNode and its parent as parent.
• If currentNode is the root node: // If parent is
// NULL
a. Make ROOT point to NULL.
. 52 . b. Go to step 5.
6. If currentNode is left child of parent:
. 36 . 68 . a. Make left child field of parent point to
NULL.
b. Go to step 5.
24 59 . 72 . 8. If currentNode is right child of parent:
a. Make right child field of parent point to
NULL.
b. Go to step 5.
. 70 80
10. Release the memory for currentNode.
parent
69
currentNode
Ver. 1.0 Session 13

109. Data Structures and Algorithms
Deleting Nodes from a Binary Search Tree (Contd.)
• Locate the node to be deleted. Mark it as
Delete node 69 currentNode and its parent as parent.
• If currentNode is the root node: // If parent is
// NULL
a. Make ROOT point to NULL.
. 52 . b. Go to step 5.
6. If currentNode is left child of parent:
. 36 . 68 . • Make left child field of parent point to
NULL.
• Go to step 5.
24 59 . 72 . 8. If currentNode is right child of parent:
a. Make right child field of parent point to
NULL.
b. Go to step 5.
. 70 80
10. Release the memory for currentNode.
parent
69
currentNode
Ver. 1.0 Session 13

110. Data Structures and Algorithms
Deleting Nodes from a Binary Search Tree (Contd.)
• Locate the node to be deleted. Mark it as
Delete node 69 currentNode and its parent as parent.
• If currentNode is the root node: // If parent is
// NULL
a. Make ROOT point to NULL.
. 52 . b. Go to step 5.
6. If currentNode is left child of parent:
. 36 . 68 . • Make left child field of parent point to
NULL.
• Go to step 5.
24 59 . 72 . 8. If currentNode is right child of parent:
a. Make right child field of parent point to
NULL.
b. Go to step 5.
. 70 80
• Release the memory for currentNode.
parent
69
currentNode
Ver. 1.0 Session 13

111. Data Structures and Algorithms
Deleting Nodes from a Binary Search Tree (Contd.)
• Locate the node to be deleted. Mark it as
Delete node 69 currentNode and its parent as parent.
• If currentNode is the root node: // If parent is
// NULL
a. Make ROOT point to NULL.
. 52 . b. Go to step 5.
6. If currentNode is left child of parent:
. 36 . 68 . a. Make left child field of parent point to
NULL.
b. Go to step 5.
24 59 . 72 . 8. If currentNode is right child of parent:
a. Make right child field of parent point to
NULL.
b. Go to step 5.
. 70 80
10. Release the memory for currentNode.
parent
69
Delete operation complete
currentNode
Ver. 1.0 Session 13

112. Data Structures and Algorithms
Deleting Nodes from a Binary Search Tree (Contd.)
Write an algorithm to delete a node, which has one child
from a binary search tree.
Ver. 1.0 Session 13

113. Data Structures and Algorithms
Deleting Nodes from a Binary Search Tree (Contd.)
1. Locate the node to be deleted. Mark it as
currentNode and its parent as parent.
Delete node delete a node
Algorithm to 80
with one child. 3. If currentNode has a left child:
a. Mark the left child of currentNode as
root child.
b. Go to step 4.
. 52 .
5. If currentNode has a right child:
a. Mark the right child of currentNode as
child.
. 36 . 68 . b. Go to step 4.
7. If currentNode is the root node:
a. Mark child as root.
24 59 . 72 . b. Go to step 7.
9. If currentNode is the left child of parent:
a. Make left child field of parent point to
child.
70 . 80 b. Go to step 7.
11. If currentNode is the right child of parent:
a. Make right child field of parent point to
75 child.
b. Go to step 7.
13. Release the memory of currentNode.
Ver. 1.0 Session 13

114. Data Structures and Algorithms
Deleting Nodes from a Binary Search Tree (Contd.)
• Locate the node to be deleted. Mark it as
currentNode and its parent as parent.
Delete node 80
• If currentNode has a left child:
a. Mark the left child of currentNode as
root child.
b. Go to step 4.
. 52 .
5. If currentNode has a right child:
a. Mark the right child of currentNode as
child.
. 36 . 68 . b. Go to step 4.
parent 7. If currentNode is the root node:
a. Mark child as root.
24 59 . 72 . b. Go to step 7.
currentNode 9. If currentNode is the left child of parent:
a. Make left child field of parent point to
child.
70 . 80 b. Go to step 7.
11. If currentNode is the right child of parent:
a. Make right child field of parent point to
75 child.
b. Go to step 7.
13. Release the memory of currentNode.
Ver. 1.0 Session 13

115. Data Structures and Algorithms
Deleting Nodes from a Binary Search Tree (Contd.)
• Locate the node to be deleted. Mark it as
currentNode and its parent as parent.
Delete node 80
• If currentNode has a left child:
a. Mark the left child of currentNode as
root child.
b. Go to step 4.
. 52 .
5. If currentNode has a right child:
a. Mark the right child of currentNode as
child.
. 36 . 68 . b. Go to step 4.
parent 7. If currentNode is the root node:
a. Mark child as root.
24 59 . 72 . b. Go to step 7.
currentNode 9. If currentNode is the left child of parent:
a. Make left child field of parent point to
child.
70 . 80 b. Go to step 7.
11. If currentNode is the right child of parent:
a. Make right child field of parent point to
75 child.
b. Go to step 7.
13. Release the memory of currentNode.
Ver. 1.0 Session 13

116. Data Structures and Algorithms
Deleting Nodes from a Binary Search Tree (Contd.)
1. Locate the node to be deleted. Mark it as
currentNode and its parent as parent.
Delete node 80
3. If currentNode has a left child:
• Mark the left child of currentNode as
root child.
• Go to step 4.
. 52 .
5. If currentNode has a right child:
a. Mark the right child of currentNode as
child.
. 36 . 68 . b. Go to step 4.
parent 7. If currentNode is the root node:
a. Mark child as root.
24 59 . 72 . b. Go to step 7.
currentNode 9. If currentNode is the left child of parent:
a. Make left child field of parent point to
child.
70 . 80 b. Go to step 7.
11. If currentNode is the right child of parent:
a. Make right child field of parent point to
75 child.
b. Go to step 7.
child 13. Release the memory of currentNode.
Ver. 1.0 Session 13

117. Data Structures and Algorithms
Deleting Nodes from a Binary Search Tree (Contd.)
1. Locate the node to be deleted. Mark it as
currentNode and its parent as parent.
Delete node 80
3. If currentNode has a left child:
• Mark the left child of currentNode as
root child.
• Go to step 4.
. 52 .
5. If currentNode has a right child:
a. Mark the right child of currentNode as
child.
. 36 . 68 . b. Go to step 4.
parent 7. If currentNode is the root node:
a. Mark child as root.
24 59 . 72 . b. Go to step 7.
currentNode 9. If currentNode is the left child of parent:
a. Make left child field of parent point to
child.
70 . 80 b. Go to step 7.
11. If currentNode is the right child of parent:
a. Make right child field of parent point to
75 child.
b. Go to step 7.
child 13. Release the memory of currentNode.
Ver. 1.0 Session 13

118. Data Structures and Algorithms
Deleting Nodes from a Binary Search Tree (Contd.)
1. Locate the node to be deleted. Mark it as
currentNode and its parent as parent.
Delete node 80
3. If currentNode has a left child:
a. Mark the left child of currentNode as
root child.
b. Go to step 4.
. 52 .
5. If currentNode has a right child:
a. Mark the right child of currentNode as
child.
. 36 . 68 . b. Go to step 4.
parent 7. If currentNode is the root node:
a. Mark child as root.
24 59 . 72 . b. Go to step 7.
currentNode 9. If currentNode is the left child of parent:
a. Make left child field of parent point to
child.
70 . 80 b. Go to step 7.
11. If currentNode is the right child of parent:
a. Make right child field of parent point to
75 child.
b. Go to step 7.
child 13. Release the memory of currentNode.
Ver. 1.0 Session 13

119. Data Structures and Algorithms
Deleting Nodes from a Binary Search Tree (Contd.)
1. Locate the node to be deleted. Mark it as
currentNode and its parent as parent.
Delete node 80
3. If currentNode has a left child:
a. Mark the left child of currentNode as
root child.
b. Go to step 4.
. 52 .
5. If currentNode has a right child:
a. Mark the right child of currentNode as
child.
. 36 . 68 . b. Go to step 4.
parent 7. If currentNode is the root node:
a. Mark child as root.
24 59 . 72 . b. Go to step 7.
currentNode 9. If currentNode is the left child of parent:
a. Make left child field of parent point to
child.
70 . 80 b. Go to step 7.
11. If currentNode is the right child of parent:
a. Make right child field of parent point to
75 child.
b. Go to step 7.
child 13. Release the memory of currentNode.
Ver. 1.0 Session 13

120. Data Structures and Algorithms
Deleting Nodes from a Binary Search Tree (Contd.)
1. Locate the node to be deleted. Mark it as
currentNode and its parent as parent.
Delete node 80
3. If currentNode has a left child:
a. Mark the left child of currentNode as
root child.
b. Go to step 4.
. 52 .
5. If currentNode has a right child:
a. Mark the right child of currentNode as
child.
. 36 . 68 . b. Go to step 4.
parent 7. If currentNode is the root node:
a. Mark child as root.
24 59 . 72 . b. Go to step 7.
currentNode 9. If currentNode is the left child of parent:
a. Make left child field of parent point to
child.
70 . 80 b. Go to step 7.
11. If currentNode is the right child of parent:
a. Make right child field of parent point to
75 child.
b. Go to step 7.
child 13. Release the memory of currentNode.
Ver. 1.0 Session 13

121. Data Structures and Algorithms
Deleting Nodes from a Binary Search Tree (Contd.)
1. Locate the node to be deleted. Mark it as
currentNode and its parent as parent.
Delete node 80
3. If currentNode has a left child:
a. Mark the left child of currentNode as
root child.
b. Go to step 4.
. 52 .
5. If currentNode has a right child:
a. Mark the right child of currentNode as
child.
. 36 . 68 . b. Go to step 4.
parent 7. If currentNode is the root node:
a. Mark child as root.
24 59 . 72 . b. Go to step 7.
currentNode 9. If currentNode is the left child of parent:
a. Make left child field of parent point to
child.
70 . 80 b. Go to step 7.
11. If currentNode is the right child of parent:
• Make right child field of parent point to
75 child.
• Go to step 7.
child 13. Release the memory of currentNode.
Ver. 1.0 Session 13

122. Data Structures and Algorithms
Deleting Nodes from a Binary Search Tree (Contd.)
1. Locate the node to be deleted. Mark it as
currentNode and its parent as parent.
Delete node 80
3. If currentNode has a left child:
a. Mark the left child of currentNode as
root child.
b. Go to step 4.
. 52 .
5. If currentNode has a right child:
a. Mark the right child of currentNode as
child.
. 36 . 68 . b. Go to step 4.
parent 7. If currentNode is the root node:
a. Mark child as root.
24 59 . 72 . b. Go to step 7.
currentNode 9. If currentNode is the left child of parent:
a. Make left child field of parent point to
child.
70 . 80 b. Go to step 7.
11. If currentNode is the right child of parent:
• Make right child field of parent point to
75 child.
• Go to step 7.
child 13. Release the memory of currentNode.
Ver. 1.0 Session 13

123. Data Structures and Algorithms
Deleting Nodes from a Binary Search Tree (Contd.)
1. Locate the node to be deleted. Mark it as
currentNode and its parent as parent.
Delete node 80
3. If currentNode has a left child:
a. Mark the left child of currentNode as
root child.
b. Go to step 4.
. 52 .
5. If currentNode has a right child:
a. Mark the right child of currentNode as
child.
. 36 . 68 . b. Go to step 4.
parent 7. If currentNode is the root node:
a. Mark child as root.
24 59 . 72 . b. Go to step 7.
currentNode 9. If currentNode is the left child of parent:
a. Make left child field of parent point to
child.
70 . 80 b. Go to step 7.
11. If currentNode is the right child of parent:
a. Make right child field of parent point to
75 child.
b. Go to step 7.
Delete operation complete
child 13. Release the memory of currentNode.
Ver. 1.0 Session 13

124. Data Structures and Algorithms
Deleting Nodes from a Binary Search Tree (Contd.)
Write an algorithm to delete a node, which has two children
from a binary search tree.
Ver. 1.0 Session 13

125. Data Structures and Algorithms
Deleting Nodes from a Binary Search Tree (Contd.)
1. Locate the node to be deleted. Mark it as
currentNode and its parent as parent.
Delete node delete a node
Algorithm to 72
with two children. 3. Locate the inorder successor of currentNode.
Mark it as Inorder_suc. Execute the following
root
steps to locate Inorder_suc:
a. Mark the right child of currentNode as
. 52 . Inorder_suc.
b. Repeat until the left child of
Inorder_suc becomes NULL:
i. Make Inorder_suc point to its
. 36 . 68 . left child.
5. Replace the information held by currentNode
with that of Inorder_suc.
24 59 . 72 . 7. If the node marked Inorder_suc is a leaf
node:
a. Delete the node marked Inorder_suc
by using the algorithm for Case I.
70 . 80
8. If the node marked Inorder_suc has one
child:
a. Delete the node marked Inorder_suc
75 by using the algorithm for Case II.
Ver. 1.0 Session 13

126. Data Structures and Algorithms
Deleting Nodes from a Binary Search Tree (Contd.)
• Locate the node to be deleted. Mark it as
currentNode and its parent as parent.
Delete node 72
• Locate the inorder successor of currentNode.
Mark it as Inorder_suc. Execute the following
root
steps to locate Inorder_suc:
a. Mark the right child of currentNode as
. 52 . Inorder_suc.
b. Repeat until the left child of
parent Inorder_suc becomes NULL:
i. Make Inorder_suc point to its
. 36 . 68 . left child.
currentNode 5. Replace the information held by currentNode
with that of Inorder_suc.
24 59 . 72 . 7. If the node marked Inorder_suc is a leaf
node:
a. Delete the node marked Inorder_suc
by using the algorithm for Case I.
70 . 80
8. If the node marked Inorder_suc has one
child:
a. Delete the node marked Inorder_suc
75 by using the algorithm for Case II.
Ver. 1.0 Session 13

127. Data Structures and Algorithms
Deleting Nodes from a Binary Search Tree (Contd.)
• Locate the node to be deleted. Mark it as
currentNode and its parent as parent.
Delete node 72
• Locate the inorder successor of currentNode.
Mark it as Inorder_suc. Execute the following
root
steps to locate Inorder_suc:
a. Mark the right child of currentNode as
. 52 . Inorder_suc.
b. Repeat until the left child of
parent Inorder_suc becomes NULL:
i. Make Inorder_suc point to its
. 36 . 68 . left child.
currentNode 5. Replace the information held by currentNode
with that of Inorder_suc.
24 59 . 72 . 7. If the node marked Inorder_suc is a leaf
node:
a. Delete the node marked Inorder_suc
by using the algorithm for Case I.
70 . 80
8. If the node marked Inorder_suc has one
child:
a. Delete the node marked Inorder_suc
75 by using the algorithm for Case II.
Ver. 1.0 Session 13

128. Data Structures and Algorithms
Deleting Nodes from a Binary Search Tree (Contd.)
1. Locate the node to be deleted. Mark it as
currentNode and its parent as parent.
Delete node 72
3. Locate the inorder successor of currentNode.
Mark it as Inorder_suc. Execute the following
root
steps to locate Inorder_suc:
• Mark the right child of currentNode as
. 52 . Inorder_suc.
• Repeat until the left child of
parent Inorder_suc becomes NULL:
i. Make Inorder_suc point to its
. 36 . 68 . left child.
currentNode 5. Replace the information held by currentNode
with that of Inorder_suc.
24 59 . 72 . 7. If the node marked Inorder_suc is a leaf
node:
a. Delete the node marked Inorder_suc
by using the algorithm for Case I.
70 . 80
8. If the node marked Inorder_suc has one
child:
Inorder_suc a. Delete the node marked Inorder_suc
75 by using the algorithm for Case II.
Ver. 1.0 Session 13

129. Data Structures and Algorithms
Deleting Nodes from a Binary Search Tree (Contd.)
1. Locate the node to be deleted. Mark it as
currentNode and its parent as parent.
Delete node 72
3. Locate the inorder successor of currentNode.
Mark it as Inorder_suc. Execute the following
root
steps to locate Inorder_suc:
• Mark the right child of currentNode as
. 52 . Inorder_suc.
• Repeat until the left child of
parent Inorder_suc becomes NULL:
i. Make Inorder_suc point to its
. 36 . 68 . left child.
currentNode 5. Replace the information held by currentNode
with that of Inorder_suc.
24 59 . 72 . 7. If the node marked Inorder_suc is a leaf
node:
a. Delete the node marked Inorder_suc
by using the algorithm for Case I.
70 . 80
8. If the node marked Inorder_suc has one
child:
Inorder_suc a. Delete the node marked Inorder_suc
75 by using the algorithm for Case II.
Ver. 1.0 Session 13

130. Data Structures and Algorithms
Deleting Nodes from a Binary Search Tree (Contd.)
1. Locate the node to be deleted. Mark it as
currentNode and its parent as parent.
Delete node 72
3. Locate the inorder successor of currentNode.
Mark it as Inorder_suc. Execute the following
root
steps to locate Inorder_suc:
a. Mark the right child of currentNode as
. 52 . Inorder_suc.
b. Repeat until the left child of
parent Inorder_suc becomes NULL:
i. Make Inorder_suc point to its
. 36 . 68 . left child.
currentNode 5. Replace the information held by currentNode
with that of Inorder_suc.
24 59 . 72 . 7. If the node marked Inorder_suc is a leaf
node:
a. Delete the node marked Inorder_suc
by using the algorithm for Case I.
70 . 80
8. If the node marked Inorder_suc has one
child:
Inorder_suc a. Delete the node marked Inorder_suc
75 by using the algorithm for Case II.
Inorder_suc
Ver. 1.0 Session 13

131. Data Structures and Algorithms
Deleting Nodes from a Binary Search Tree (Contd.)
1. Locate the node to be deleted. Mark it as
currentNode and its parent as parent.
Delete node 72
3. Locate the inorder successor of currentNode.
Mark it as Inorder_suc. Execute the following
root
steps to locate Inorder_suc:
a. Mark the right child of currentNode as
. 52 . Inorder_suc.
b. Repeat until the left child of
parent Inorder_suc becomes NULL:
i. Make Inorder_suc point to its
. 36 . 68 . left child.
currentNode • Replace the information held by currentNode
with that of Inorder_suc.
24 59 . 72
75 . • If the node marked Inorder_suc is a leaf
node:
a. Delete the node marked Inorder_suc
by using the algorithm for Case I.
70 . 80
8. If the node marked Inorder_suc has one
child:
a. Delete the node marked Inorder_suc
75 by using the algorithm for Case II.
Inorder_suc
Ver. 1.0 Session 13

132. Data Structures and Algorithms
Deleting Nodes from a Binary Search Tree (Contd.)
1. Locate the node to be deleted. Mark it as
currentNode and its parent as parent.
Delete node 72
3. Locate the inorder successor of currentNode.
Mark it as Inorder_suc. Execute the following
root
steps to locate Inorder_suc:
a. Mark the right child of currentNode as
. 52 . Inorder_suc.
b. Repeat until the left child of
parent Inorder_suc becomes NULL:
i. Make Inorder_suc point to its
. 36 . 68 . left child.
currentNode • Replace the information held by currentNode
with that of Inorder_suc.
24 59 . 75 . • If the node marked Inorder_suc is a leaf
node:
a. Delete the node marked Inorder_suc
by using the algorithm for Case I.
70 . 80
8. If the node marked Inorder_suc has one
child:
a. Delete the node marked Inorder_suc
75 by using the algorithm for Case II.
Inorder_suc
Ver. 1.0 Session 13

133. Data Structures and Algorithms
Deleting Nodes from a Binary Search Tree (Contd.)
1. Locate the node to be deleted. Mark it as
currentNode and its parent as parent.
Delete node 72:
3. Locate the inorder successor of currentNode.
Mark it as Inorder_suc. Execute the following
root
steps to locate Inorder_suc:
a. Mark the right child of currentNode as
. 52 . Inorder_suc.
b. Repeat until the left child of
parent Inorder_suc becomes NULL:
i. Make Inorder_suc point to its
. 36 . 68 . left child.
currentNode 5. Replace the information held by currentNode
with that of Inorder_suc.
24 59 . 75 . 7. If the node marked Inorder_suc is a leaf
node:
a. Delete the node marked Inorder_suc
by using the algorithm for Case I.
70 . 80
8. If the node marked Inorder_suc has one
child:
a. Delete the node marked Inorder_suc
75 by using the algorithm for Case II.
Delete operation complete
Inorder_suc
Ver. 1.0 Session 13

134. Data Structures and Algorithms
Activity: Implementing a Binary Search Tree
Problem Statement:
Write a program to implement insert and traverse operations
on a binary search tree that contains the words in a dictionary.
Ver. 1.0 Session 13

135. Data Structures and Algorithms
Summary
In this session, you learned that:
A tree is a nonlinear data structure that represents a
hierarchical relationship among the various data elements.
A binary tree is a specific type of tree in which each node can
have a maximum of two children.
Binary trees can be implemented by using arrays as well as
linked lists, depending upon requirement.
Traversal of a tree is the process of visiting all the nodes of the
tree once. There are three types of traversals, namely inorder,
preorder, and postorder traversal.
Binary search tree is a binary tree in which the value of the left
child of a node is always less than the value of the node, and
the value of the right child of a node is greater than the value of
the node.
Ver. 1.0 Session 13

136. Data Structures and Algorithms
Summary (Contd.)
Inserting a node in a binary search tree requires you to first
locate the appropriate position for the node to be inserted.
You need to check for the following three cases before deleting
a node from a binary search tree.
If the node to be deleted is the leaf node
If the node to be deleted has one child (left or right)
If the node to be deleted has two children
Ver. 1.0 Session 13