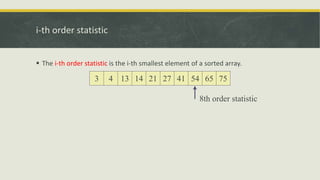
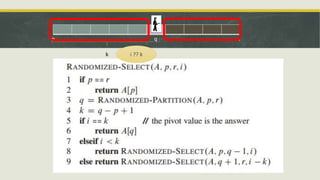
This document discusses order statistics and medians. It defines the i-th order statistic as the i-th smallest element of a sorted array. The median is defined as the halfway point of a data set. For an odd number of elements, the median is the (n+1)/2 order statistic, and for an even number it is defined as the average of the n/2 and n/2+1 order statistics. Methods for finding the minimum and maximum in expected linear time using pairs are presented. Selection algorithms for finding the k-th order statistic in expected and worst-case linear time using techniques like median of medians are also summarized.

1. Medians
and Order Statistics
Teacher: Nguyen Van Tuyen
Student: Nguyen Phuong Hoa

2. Outline:
1. i-th order statistic
2. Minimum and maximum
3. Selection Problem
a. Selection in expected linear time
b. Selection in worst-case linear time
4.Q&A

3. i-th order statistic
 The i-th order statistic is the i-th smallest element of a sorted array.
8th order statistic
3 4 13 14 21 27 41 54 65 75

4. Median
 Median is a halfway point of the set.
 N is odd, median is (n+1)/2-th order statistic
 N is even,
upper median
3 4 13 14 23 27 41
lower median
54 65 75
The lower median is the
𝑛+1
2
-th order statistic
The upper median is the
𝑛+1
2
-th order statistic

5. Minimum and maximum
 Can do with 2n-2 comparisons.
 Can do better 3 𝑛/2
 Form pairs of elements
 Compare elements in each pair
 Pair (ai, ai+1), assume ai < ai+1, then
 Compare (min,ai), (ai+1,max)
 3 comparisions for each pair.
How many comparisons are necessary
to determine the minimum and
maximum of a set of n-elements?

6. Minimum and maximum
Show that the second smallest of n-elements
can be found with n+ lgn -2
comparisons in the worst case???

7. Selection Problem
Can sort first – (n lg n), but can do better – (n).

8. p rq
k i ?? k

9. Selection in expected linear time
 Worst-case: O(n^2)
 Best-case: O(n)
 Average case: O(n)

10. Selection in worst-case linear time

11. Selection in worst-case linear time
1. Group the given number in subsets of 5 in O(n) time
2. Find the median of each of the n=5 groups and then picking the median from the
sorted list of group elements.
3. Use SELECT recursively to find the median x of the n=5 medians found in step 2
4. Partition the input array around the median-of-median x using the modified version of
PARTITION. Let k be one more than the number of elements on the low side of the
partition, so that x is the kth smallest element and there are n-k elements on the high
side of the partition.
5. If i = k, then return x. Otherwise, use SELECT recursively to find the ith smallest
element on the low side if i<k,or the (i-k)th smallest element on the high side if i>k.
If n is small, (n<6) just sort and
return the k-th smallest number in
constant time  O(1) time.

12. 2 5 64 24 44
1 4 6 9 20
21 95 36 8 7
4 24 3 56 8
12 13 17 18 89
1 4 3 8 7
2 5 6 9 8
4 13 17 18 20
12 24 36 24 44
21 95 64 56 89

13. Key points
 i-th order statistic
 Median
 Minimum and maximum
 Selection Problem

14. Q&A