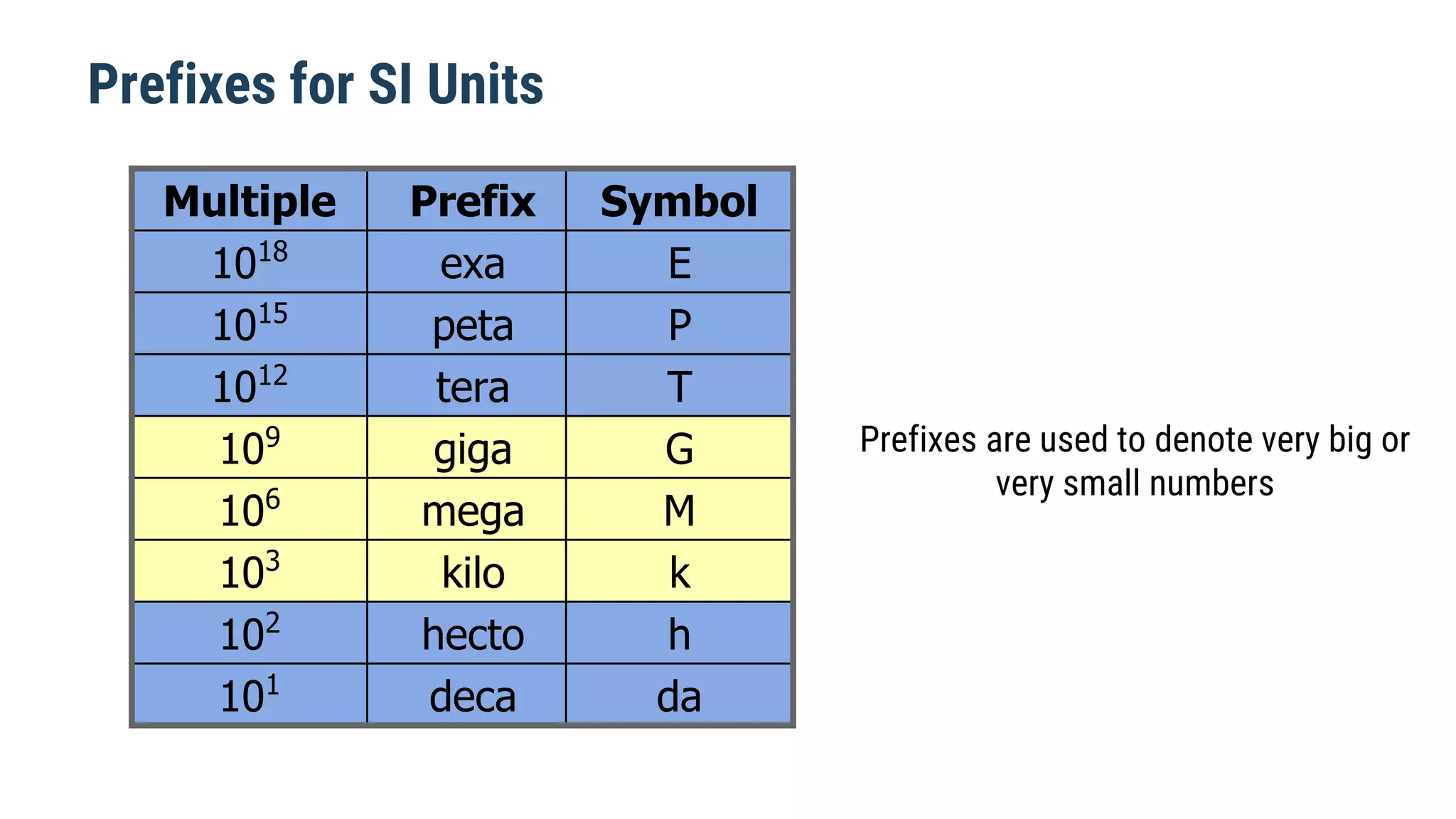
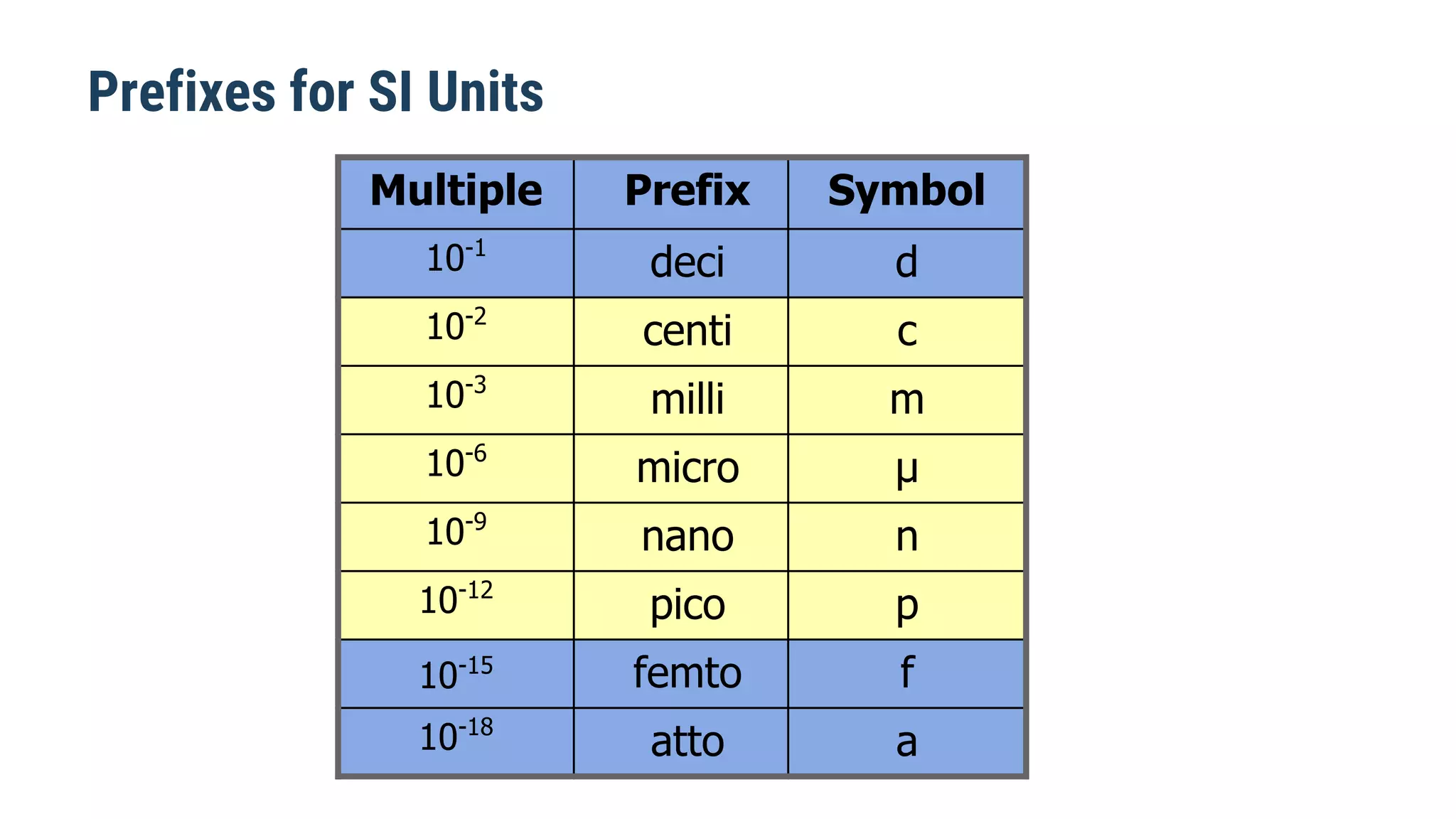
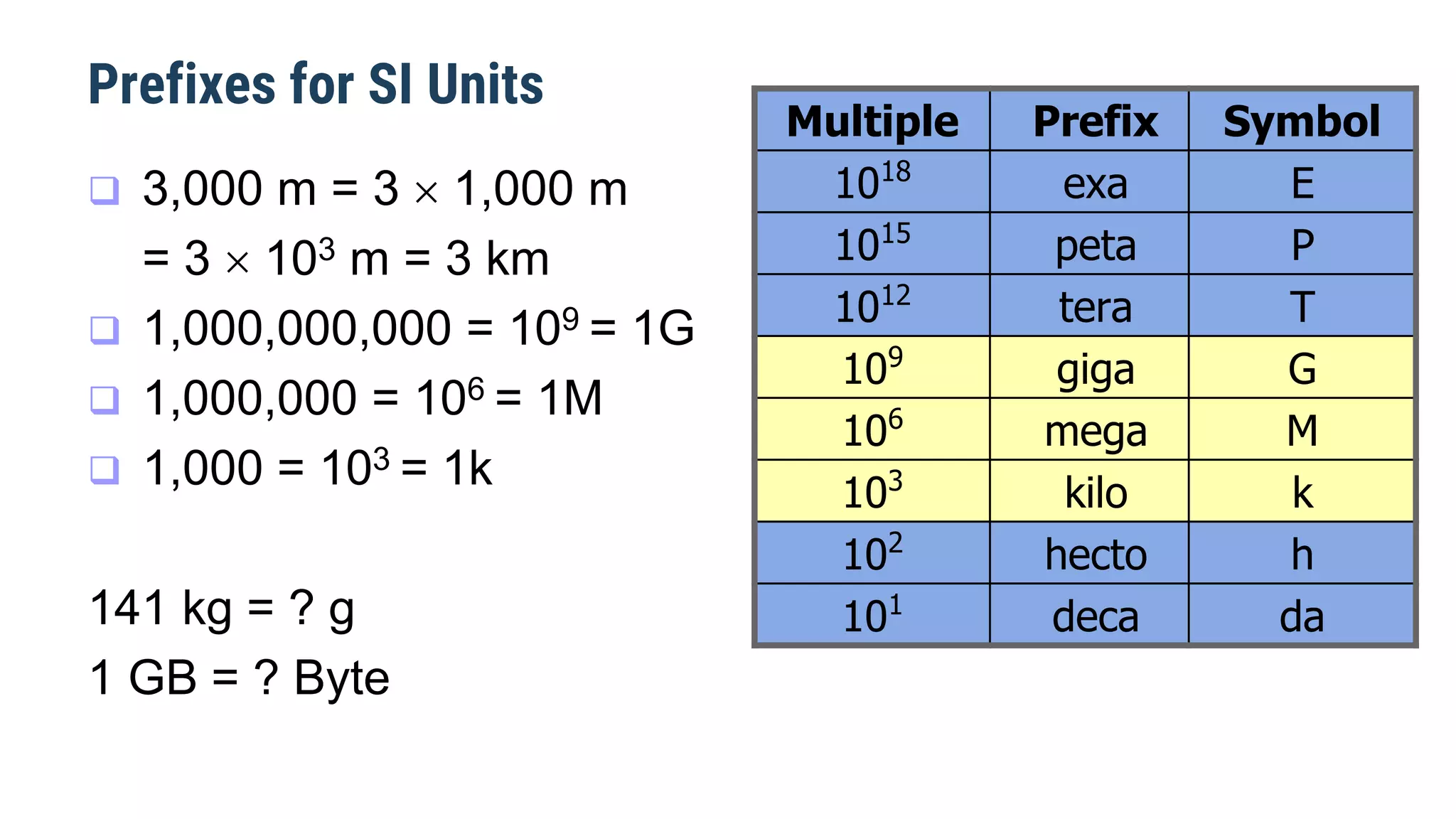
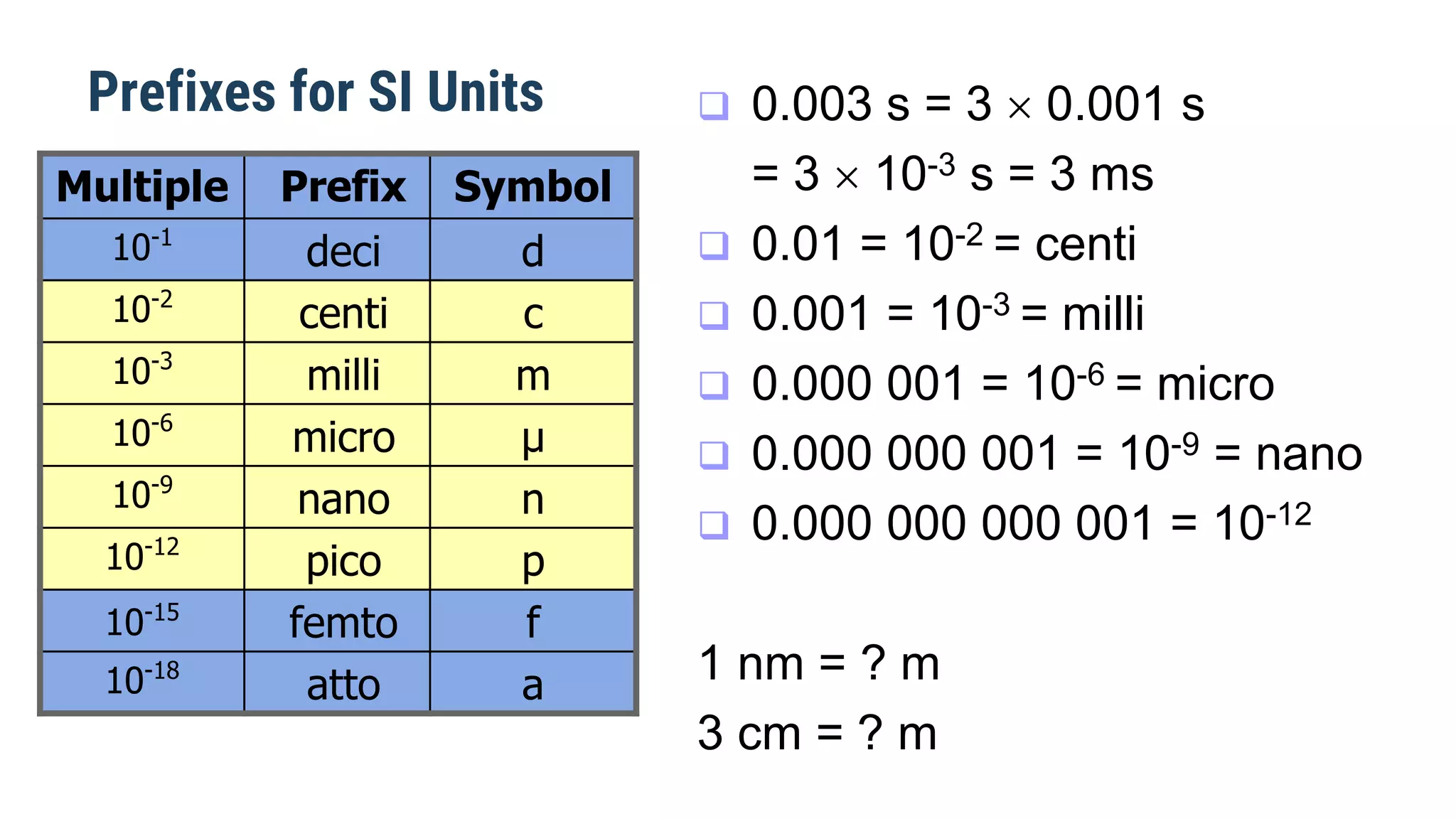
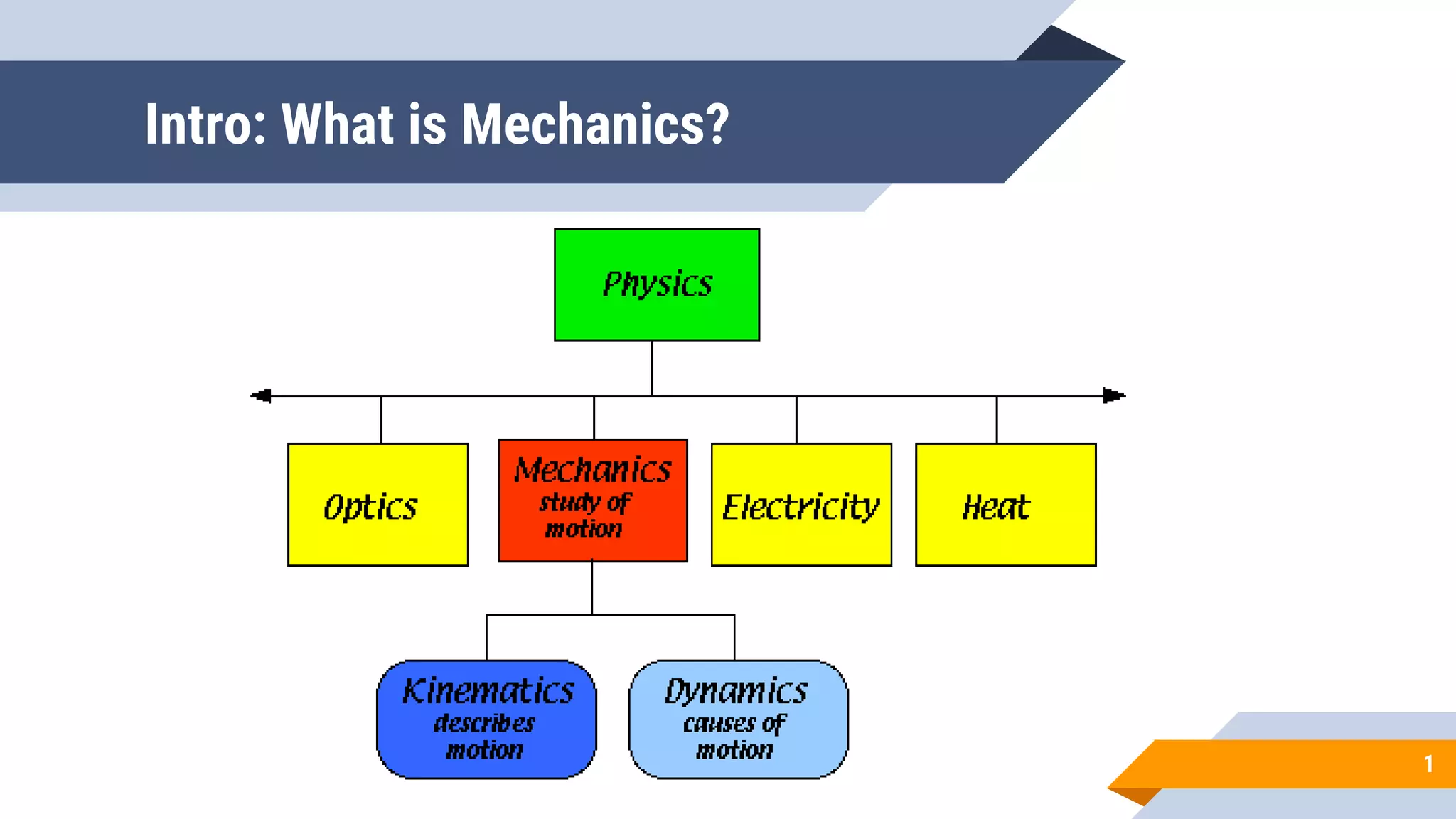
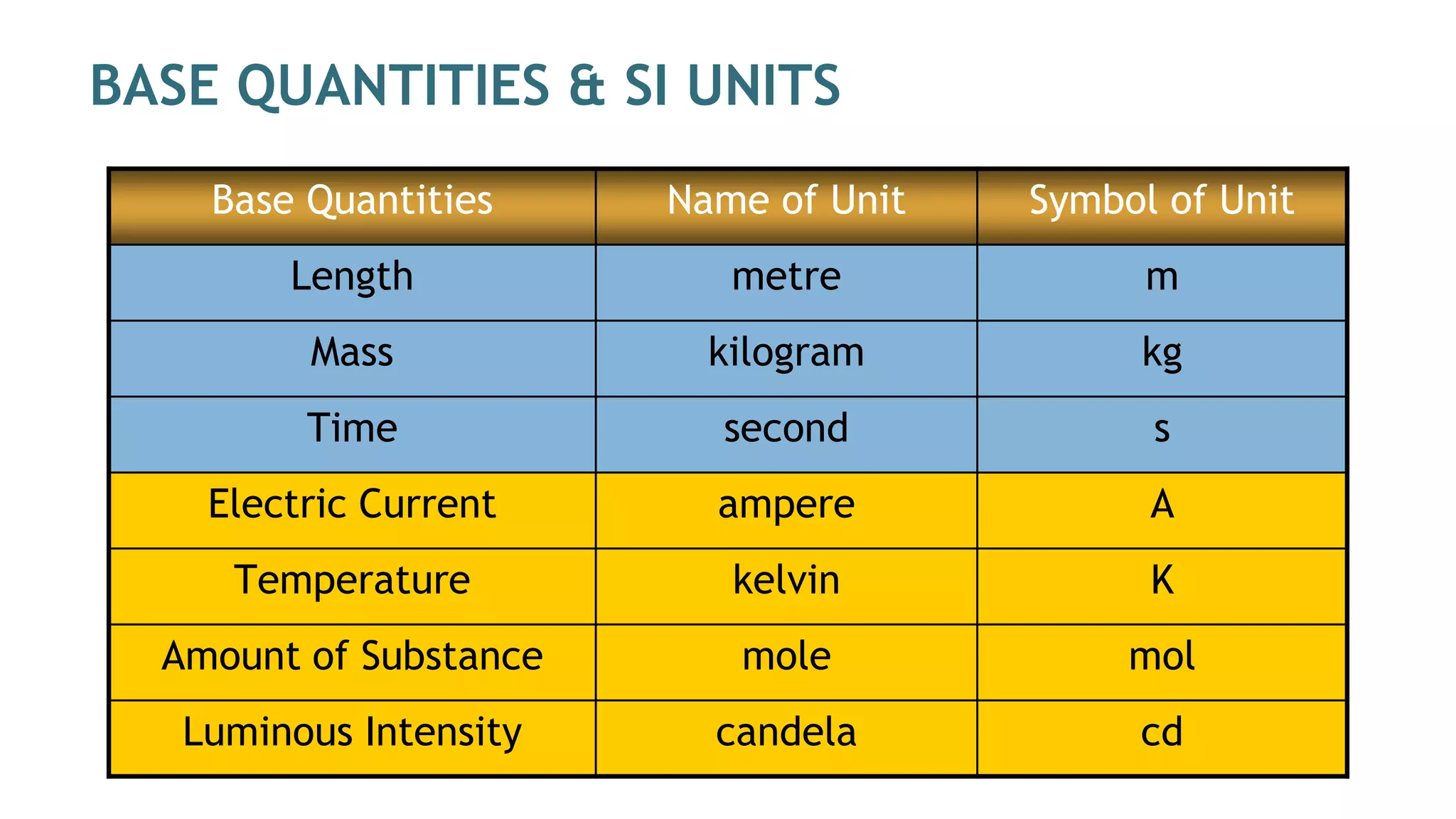
Mechanics is the branch of physics dealing with the study of motion. It can be divided into kinematics, which deals with describing motions, and dynamics, which deals with the causes of motion. The International System of Units (SI) provides standardized units for measuring physical quantities. The three base SI units are the meter (length), kilogram (mass), and second (time). Derived quantities like area, speed, and density can be calculated using the appropriate mathematical operations and combinations of base units. Problem solving in physics requires quantifying observations with standardized units.

1. Intro: What is Mechanics?
1

2. What is Mechanics?
2
▰ Mechanics is the branch of Physics dealing with the
study of motion
▰ Motion is a fundamental idea in all of science.
▰ Mechanics can be divided into 2 areas:
1. Kinematics, dealing with describing motions
2. Dynamics, dealing with the causes of motion

3. CHAPTER
UNITS AND PROBLEM SOLVING
3
1

4. CHAPTER OBJECTIVE
▰ Distinguish standard unit and system units
▰ Describe the SI and specify the references for the three main base quantities of
this system
▰ Use common metric prefixes and nonstandard metric units
▰ Explain conversion factor relationships and apply them in converting units
within a system
▰ Determine the number of significant figures
▰ Establish a problem-solving procedure and apply it to typical problems
4

5. Quantitative Observations
What can be measured with the
instruments on an aeroplane?
Qualitative Observations
How do you measure artistic
beauty?
Observation: Quantitative vs qualitative
• Most observation in physics are quantitative
• Descriptive observations (or qualitative) are usually imprecise

6. ▰ To be quantitative in Physics requires measurements
▰ How tall is Ming Yao? How about his weight?
▻ Height: 2.29 m (7 ft 6 in)
▻ Weight: 141 kg (310 lb)
Number + Unit
▰ Unit officially accepted – standard unit
▰ A group of standard unit/combination – system of units
▰ Both numbers and units necessary for any meaningful
physical quantities
Why & How We Measure: Physical Quantities

7. Are classified into two types:
1. Base quantities
2. Derived quantities
Physical Quantities
Base quantity
is like the brick – the
basic building block of
a house
Derived quantity is like
the house that was
build up from a collection
of bricks (basic quantity)

8. ▰ Many possible choices for units of Length, Mass, Time (e.g.
Yao is 2.29 m or 7 ft 6 in.)
▰ In 1960, standards bodies control and define System
Internationale (SI) unit:
Eg.
▻ LENGTH: Meter
▻ MASS: Kilogram
▻ TIME: Second
SI UNITS

9. BASE QUANTITIES & SI UNITS
Base Quantities Name of Unit Symbol of Unit
Length metre m
Mass kilogram kg
Time second s
Electric Current ampere A
Temperature kelvin K
Amount of Substance mole mol
Luminous Intensity candela cd

10. SI Length Unit: Meter
▰ Length describe the quantity of space such width, height or
distance
▰ Symbol  [L]
▰ Current Definition of 1 Meter: the distance traveled by light
in vacuum during a time of 1/299,792,458 second.
▰ 1 Meter = about 3.28 ft
▰ 1 km = 1000 m, 1 cm = 1/100 m, 1 mm = 1/1000 m

11. SI Time Unit: Second
▰ Time describes the flow of the universe from the past through
the present into the future. In physics, usually mean a quantity
of time in seconds, such as 35s.
▰ Symbol  [T]
▰ The solar clock was originally used to define the second.
▰ 1 Second is defined in terms of an “atomic clock”– time taken
for 9,192,631,770 oscillations of the light emitted by a
cesium-133 atom.

12. Atomic Clock
▰ Louis Essen (right) and
Jack Parry (left) standing
next to the world's first
caesium-133 atomic clock

13. SI Mass Unit: Kilogram
▰ Mass describes the quantity of matter
▰ Symbol  [M]
▰ 1 Kilogram – the mass of a specific platinum-
iridium alloy kept at International Bureau of
Weights and Measures near Paris. Copies are
kept in many other countries.
▰ Yao Ming is 141 kg, equivalent to weight of 141
pieces of the alloy cylinder.

14. Length, Mass, Time

15. Prefixes for SI Units
Multiple Prefix Symbol
1018
exa E
1015
peta P
1012
tera T
109
giga G
106
mega M
103
kilo k
102
hecto h
101
deca da
Prefixes are used to denote very big or
very small numbers

16. Multiple Prefix Symbol
10-1
deci d
10-2
centi c
10-3
milli m
10-6
micro µ
10-9
nano n
10-12
pico p
10-15
femto f
10-18
atto a
Prefixes for SI Units

17. Prefixes for SI Units
Multiple Prefix Symbol
1018
exa E
1015
peta P
1012
tera T
109
giga G
106
mega M
103
kilo k
102
hecto h
101
deca da
 3,000 m = 3  1,000 m
= 3  103 m = 3 km
 1,000,000,000 = 109 = 1G
 1,000,000 = 106 = 1M
 1,000 = 103 = 1k
141 kg = ? g
1 GB = ? Byte

18. Multiple Prefix Symbol
10-1
deci d
10-2
centi c
10-3
milli m
10-6
micro µ
10-9
nano n
10-12
pico p
10-15
femto f
10-18
atto a
Prefixes for SI Units  0.003 s = 3  0.001 s
= 3  10-3 s = 3 ms
 0.01 = 10-2 = centi
 0.001 = 10-3 = milli
 0.000 001 = 10-6 = micro
 0.000 000 001 = 10-9 = nano
 0.000 000 000 001 = 10-12
1 nm = ? m
3 cm = ? m

19. Derived Quantities and Units
▰ Multiply and divide units just like numbers
▰ Derived quantities: area, speed, volume, density ……
▻ Area = Length  Length SI unit for area = m2
▻ Volume = Length  Length  Length SI unit for volume = m3
▻ Speed = Length / time SI unit for speed = m/s
▻ Density = Mass / Volume SI unit for density = kg/m3
▰ In 2008 Olympic Game, Usain Bolt sets world record at 9.69 s in Men’s
100 m Final. What is his average speed ?
m/s10.32
s
m
9.69
100
s9.69
m100
speed 

20. Exercise:
• Work out the derived quantities for:
Defining equation: velocity =
In terms of units: Units of speed =
Defining equation: acceleration =
In terms of units: Units of acceleration =
Defining equation: force = mass × acceleration
In terms of units: Units of force =
time
distance
time
velocity

21. 21
THANKS!
Any questions?
You can find /Whatsapp me