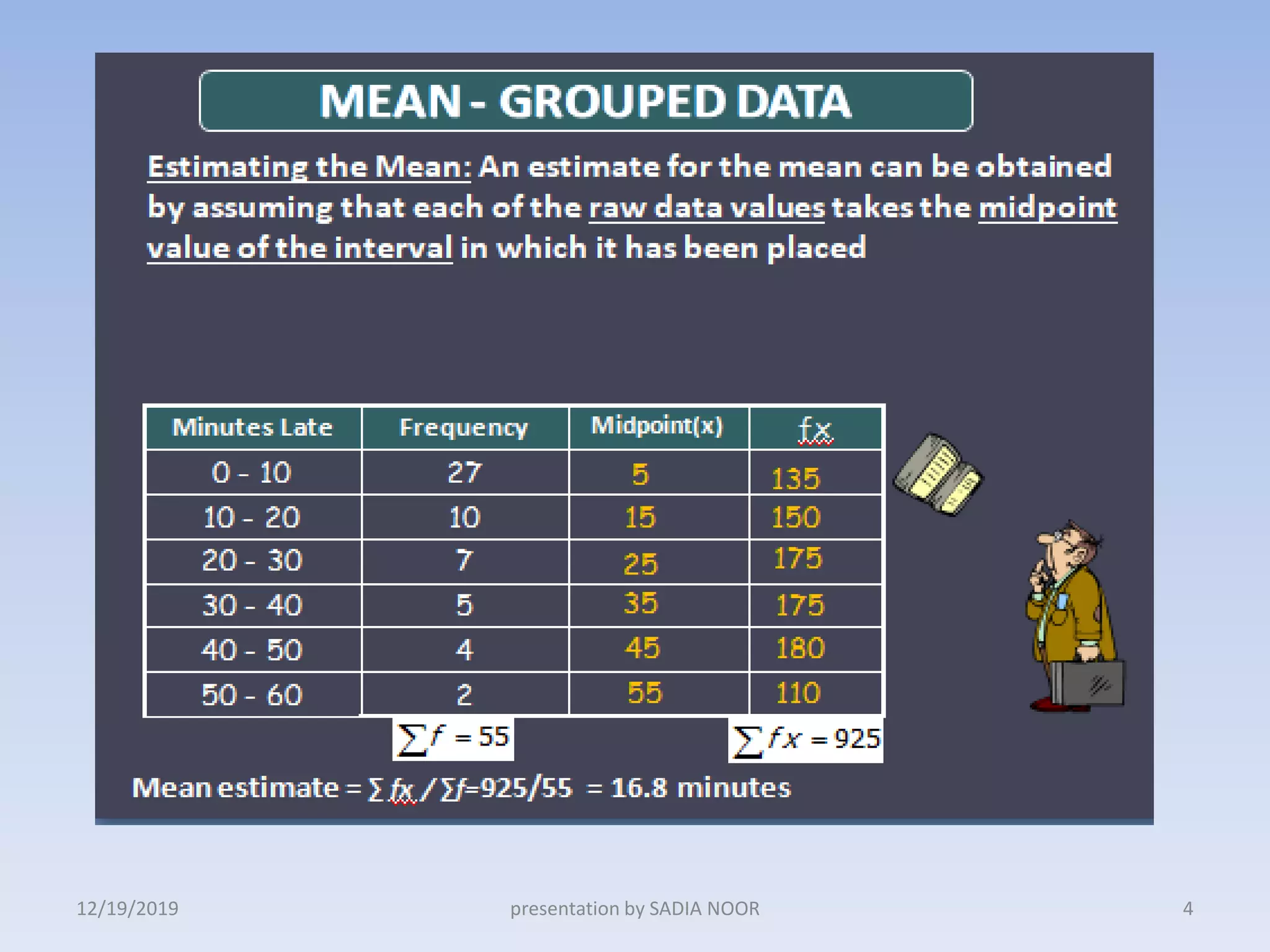
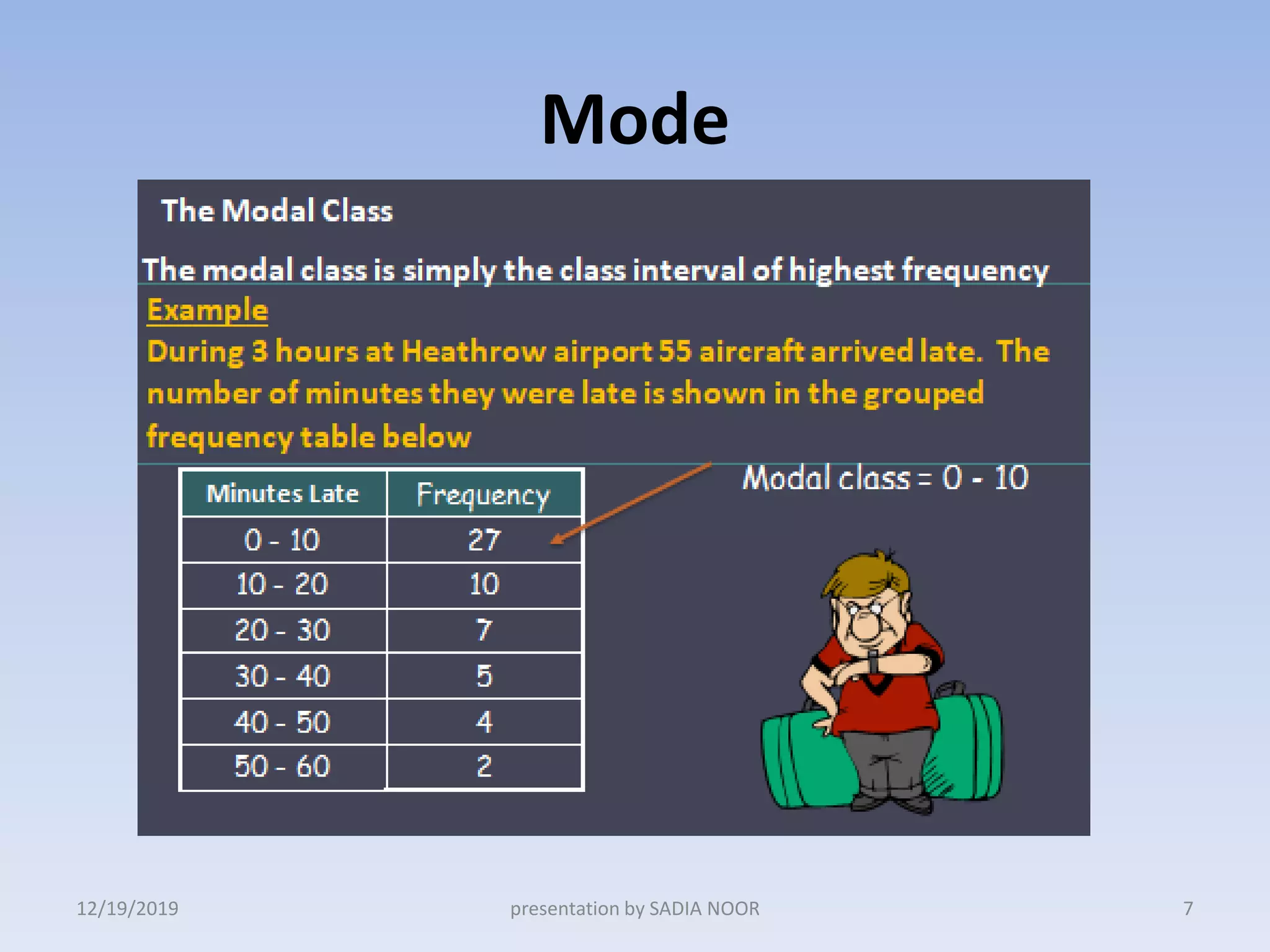
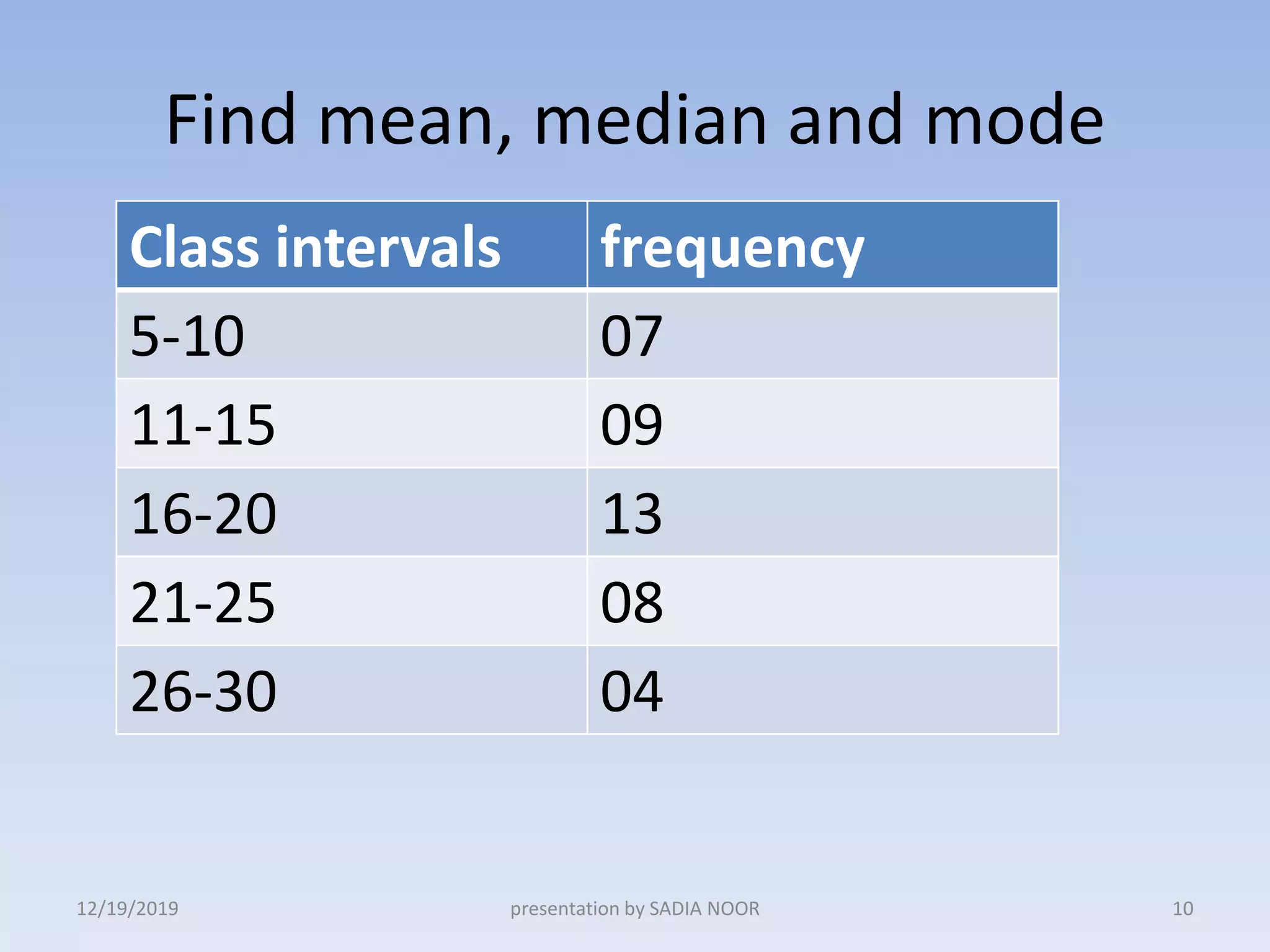
The document discusses the measurement of central tendency for grouped data, focusing on calculating the arithmetic mean, median, and mode. It includes specific formulas and examples, illustrating how to compute these measures using frequency distributions. Additionally, it explores the appropriateness of using the mean as a central measure based on the distribution's characteristics.

1. Measurement of central
tendency
Grouped data
12/19/2019 1presentation by SADIA NOOR

2. Arithmetic mean
• To find the mean of a frequency distribution
with grouped data, the product of the
frequency and the corresponding
observations (noted as fx) is calculated and
summed, that sum is then divided by the sum
of the frequency amounts.
• Mean = Ʃfx
Ʃf
12/19/2019 2presentation by SADIA NOOR

3. • Where, Ʃfx is the sum of the products of the frequency and
the corresponding observations And, Ʃf is the sum of the
frequencies.
• Example:
12/19/2019 3presentation by SADIA NOOR

4. 12/19/2019 4presentation by SADIA NOOR

5. Median
12/19/2019 5presentation by SADIA NOOR

6. • lower class boundary of median group –> l = 10
• class width of median group –> h = 10
• Frequency of median class –> f = 10
• Cumulative frequency of preceding class –> cf =
27
Median = 10 + 10/10 (55/2-27)
= 10 + 0.5
= 10.5
12/19/2019 6presentation by SADIA NOOR

7. Mode
12/19/2019 7presentation by SADIA NOOR

8. • Lower class boundary of modal group –> l = 0
• Max frequency of modal group –> fm = 27
• Preceding frequency of modal group –> f1 = 0
• Proceeding frequency of modal group –> f2 = 10
• Class Interval of modal group –> h = 10
• Mode = 0 + 27 - 0/(27- 0)+ (27 - 10)* 10
= 0 + 6.13
= 6.13
12/19/2019 8presentation by SADIA NOOR

9. Activity: find mean mode and median
12/19/2019 9presentation by SADIA NOOR

10. Find mean, median and mode
Class intervals frequency
5-10 07
11-15 09
16-20 13
21-25 08
26-30 04
12/19/2019 10presentation by SADIA NOOR

11. 12/19/2019 11Presentation by SADIA NOOR

12. Appropriate Measures of Central Tendency
• How well does the mean represent the scores in
a distribution?
• The logic here is to determine how much spread
is in the scores. How much do the scores
"deviate" from the mean? Think of the mean as
the true score or as your best guess. If every X
were very close to the Mean, the mean would be
a very good predictor.
• If the distribution is very sharply peaked then the
mean is a good measure of central tendency and
if you were to use the mean to make predictions
you would be right or close much of the time
12/19/2019 12Presentation by SADIA NOOR

13. Empirical relation between mean
median and mode
• For uni-model frequency curves which are
moderately asymmetrical we have the
relation.
• Mode = mean- 3(mean- median)
• Mode = 3median-2mean
12/19/2019 presentation by SADIA NOOR 13

14. 12/19/2019 presentation by SADIA NOOR 14