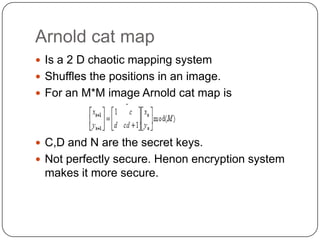
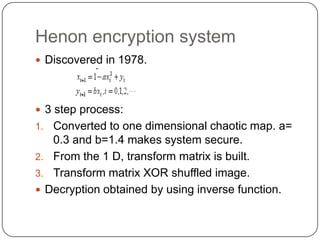
This document discusses and compares three different image encryption techniques: 1) One time padding, which uses the Vernam cipher and has a large random key space to securely transmit images. 2) Image encryption using a chaos system combined with an improved version of the DES algorithm that reduces the number of DES iterations for faster encryption. 3) Image encryption using a Henon chaotic system that first shuffles pixel positions using the Arnold cat map, then encrypts the shuffled image values. The document analyzes the security and performance of each technique.

1. Image encryption by One time
padding

2. Introduction
 Diverse usage of images
 Need to be transmitted securely over internet
 One time pad or vernam cipher
 Large random key space
 Highly secure and efficient
 Other types: RSA, El gamal
 Triple DES, Blow fish

3. Algorithm
 Chaos function:
Generates complete random values.
Small change in an initial value produces
completely different values from each other.
Example: f(x)= P*x*(1-x)
Increase in P value causes bifurcation and reaches
point of accumulation.

4. Generation of one time pads
 Starting value for the iterations
 Number for decimal places of the mantissa that
are to be supported
 Number of iterations after which the first value
can be picked
 Number of iterations to be maintained between 2
values picked.

5. Encryption methodology
 Global parameters
Indexed key table is built. Key of length 8 has 256
indexes.
 Secret parameters
4 Conditions. Shared using Diffie hellmann or RSA.
 Uses the secret parameters and run the chaotic
function.
 Every pixel of the image is XOR’ed with the
secret key.

6. Analysis
 Key space analysis
Large key space -> secure against brute force
 Statistical analysis
Histogram analysis
Correlation coefficient analysis
 Execution time
Not computational time complex
 Key sensitivity analysis
Avalanche effect.

7. Digital Image encryption based on
chaos and improved DES

8. Introduction
 Images over Internet.
 Many image encryption algorithms
 Chaos based image encryption
 Fast and highly secure image encryption
 Problem: Limited accuracy
 DES encryption: not for image encryption
 Chaos + improved DES: better encryption system

9. DES + Chaotic encryption
 Problems:
 Low speed encryption.
 500 K image data -> 14 seconds for chaotic
 500 K image data -> 467 seconds for DES
 DES lacks key space.
 Brute force attack vulnerable
 Alternate: Triple DES and AES.

10. Improved DES + Chaotic
encryption
 Reduce DES iterations to 4 speed.
 70% improvement in speed
 Security is almost negligible
 Using logistic mapping
 Random generation of keys
 Improves key space
 Tested on computer with celeron M processor
 Proves to be stronger than other image
encryptions.

11. Image encryption based on Henon
chaotic system

12. Introduction
 Similar needs as previous papers.
 Has two stages.
 Positions are shuffled
 Grey values of the image pixels are changed.
 Then the shuffled image is encrypted by Henon’s
chaotic system

13. Arnold cat map
 Is a 2 D chaotic mapping system
 Shuffles the positions in an image.
 For an M*M image Arnold cat map is
 C,D and N are the secret keys.
 Not perfectly secure. Henon encryption system
makes it more secure.

14. Henon encryption system
 Discovered in 1978.
 3 step process:
1. Converted to one dimensional chaotic map. a=
0.3 and b=1.4 makes system secure.
2. From the 1 D, transform matrix is built.
3. Transform matrix XOR shuffled image.
 Decryption obtained by using inverse function.

15. Comparison
 Image encryption by one time padding
Uses vernam cipher. Large random key space and
images are securely transmitted
 Image encryption by chaos system + improved
DES
Uses chaos system and ¼ th size of DES along
with logistic mapping for random generation of
keys.
 Image encryption by Henon chaotic system
Shuffles the image and uses henon encryption
system to make the image secure.

16. Conclusion
 Various types of image encryption techniques.
 Few of them are widely used and few of them are
still questionable.
 One time padding, Improved DES and Henon
encryption on images.
 Widely accepted -> One time padding image
encryption.

17. References
 Image encryption on chaos and improved DES
http://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arn
umber=5346839
 Image encryption on one time pads
http://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arn
umber=5591643
 Image encryption on Henon chaotic system
http://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arn
umber=5054653