Downloaded 35 times
Uploaded byAlejandro Correa Bahnsen, PhD
Maximizing a churn campaigns profitability with cost sensitive machine learning
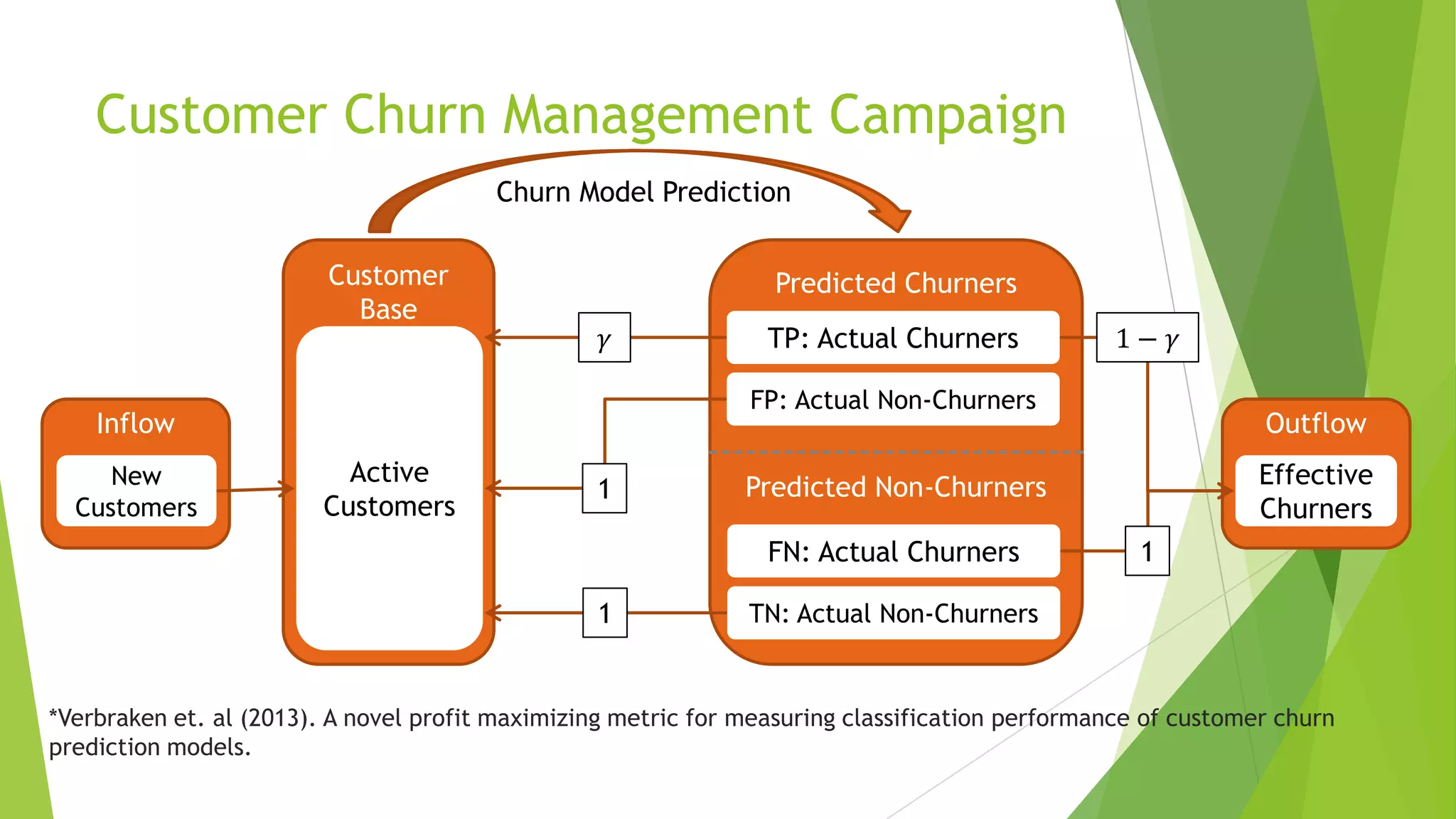
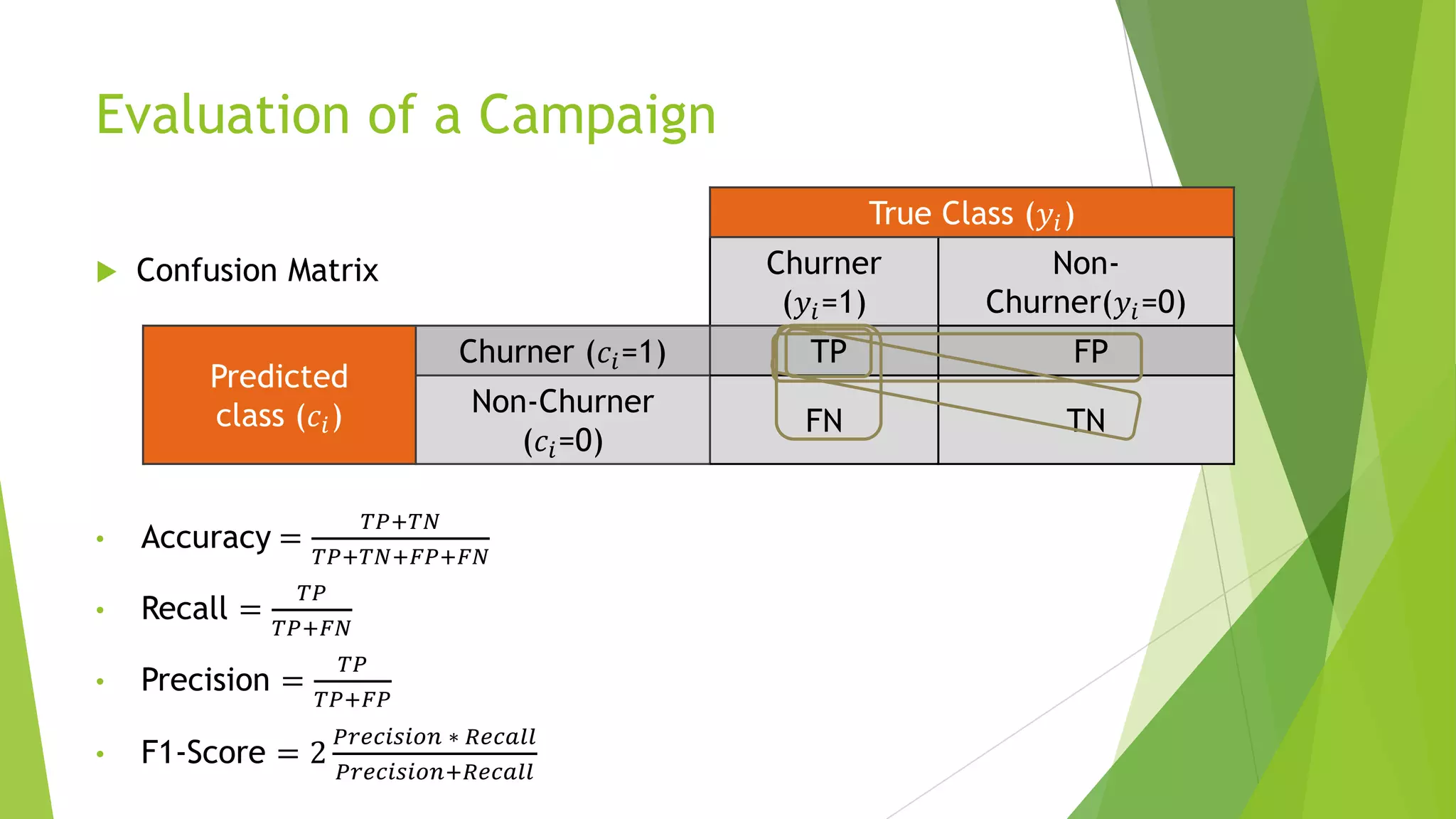
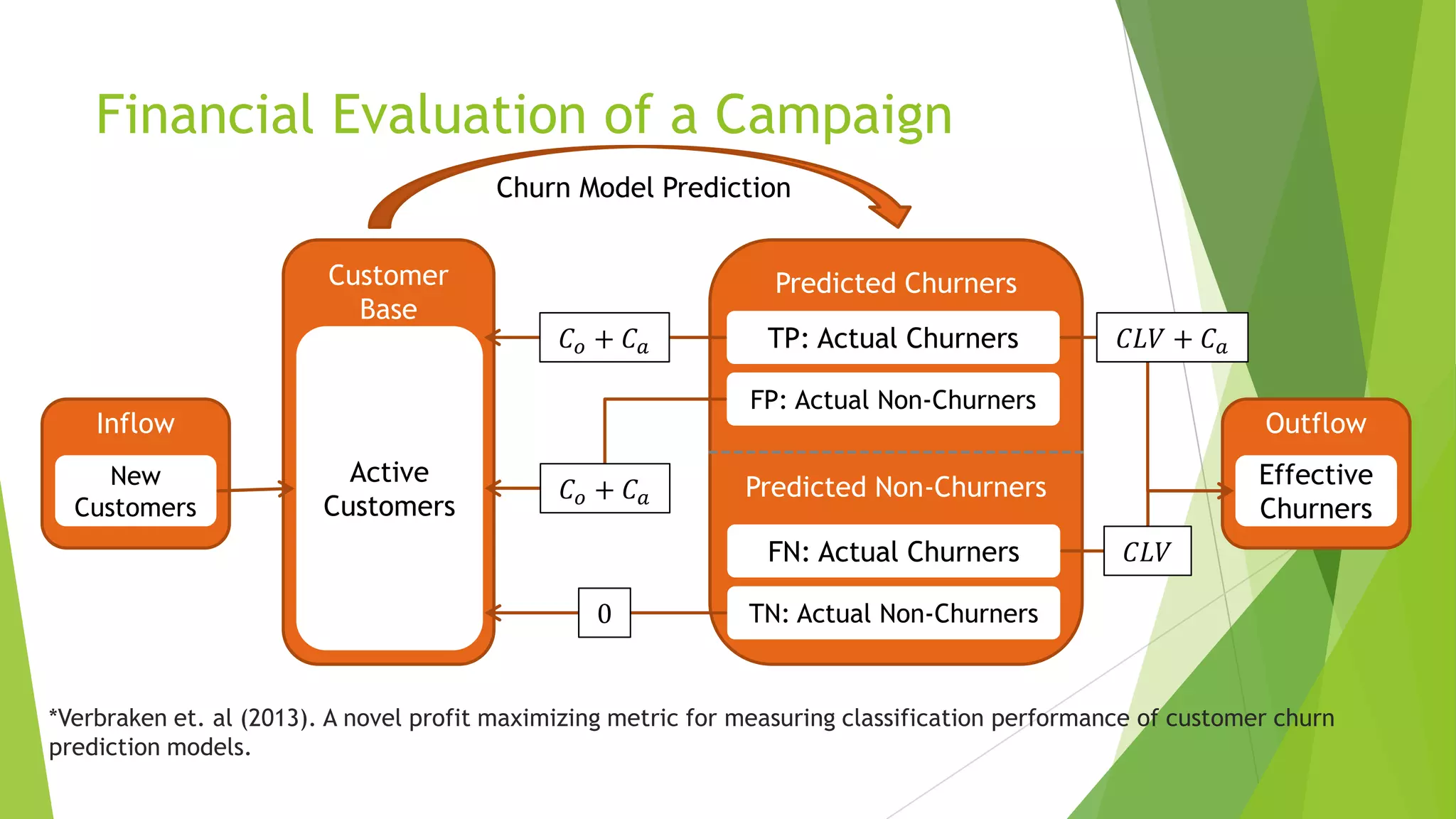
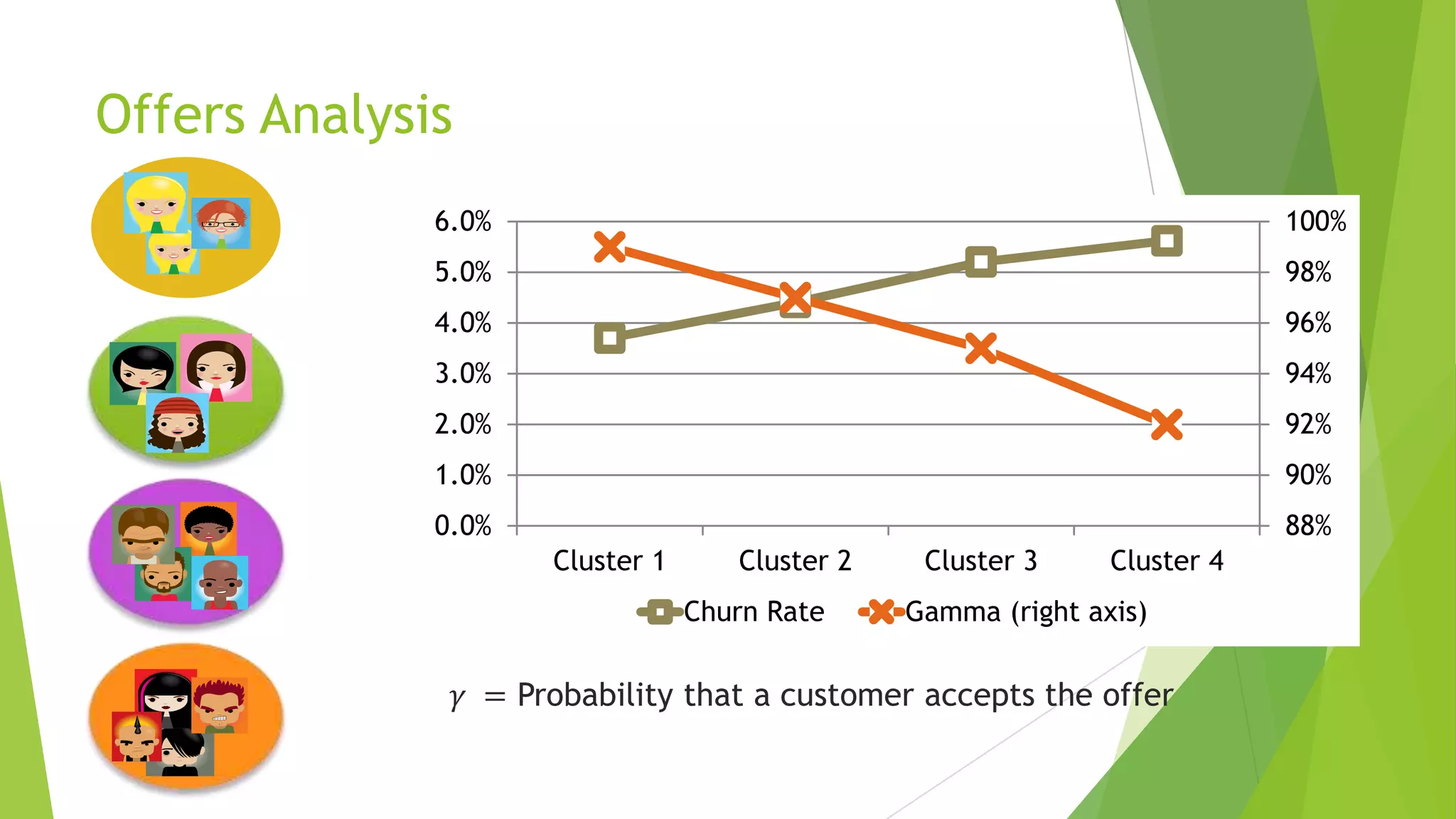
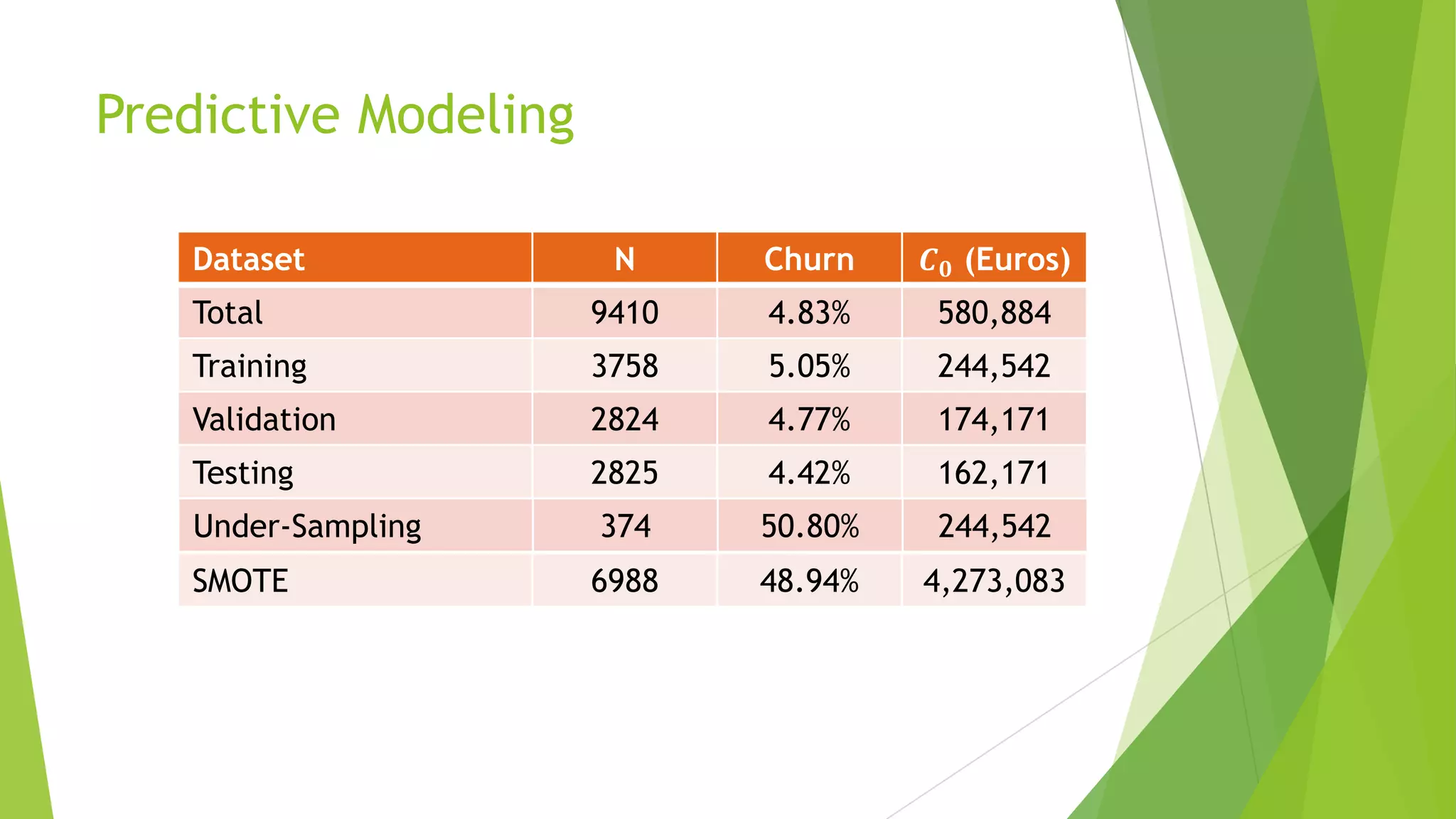
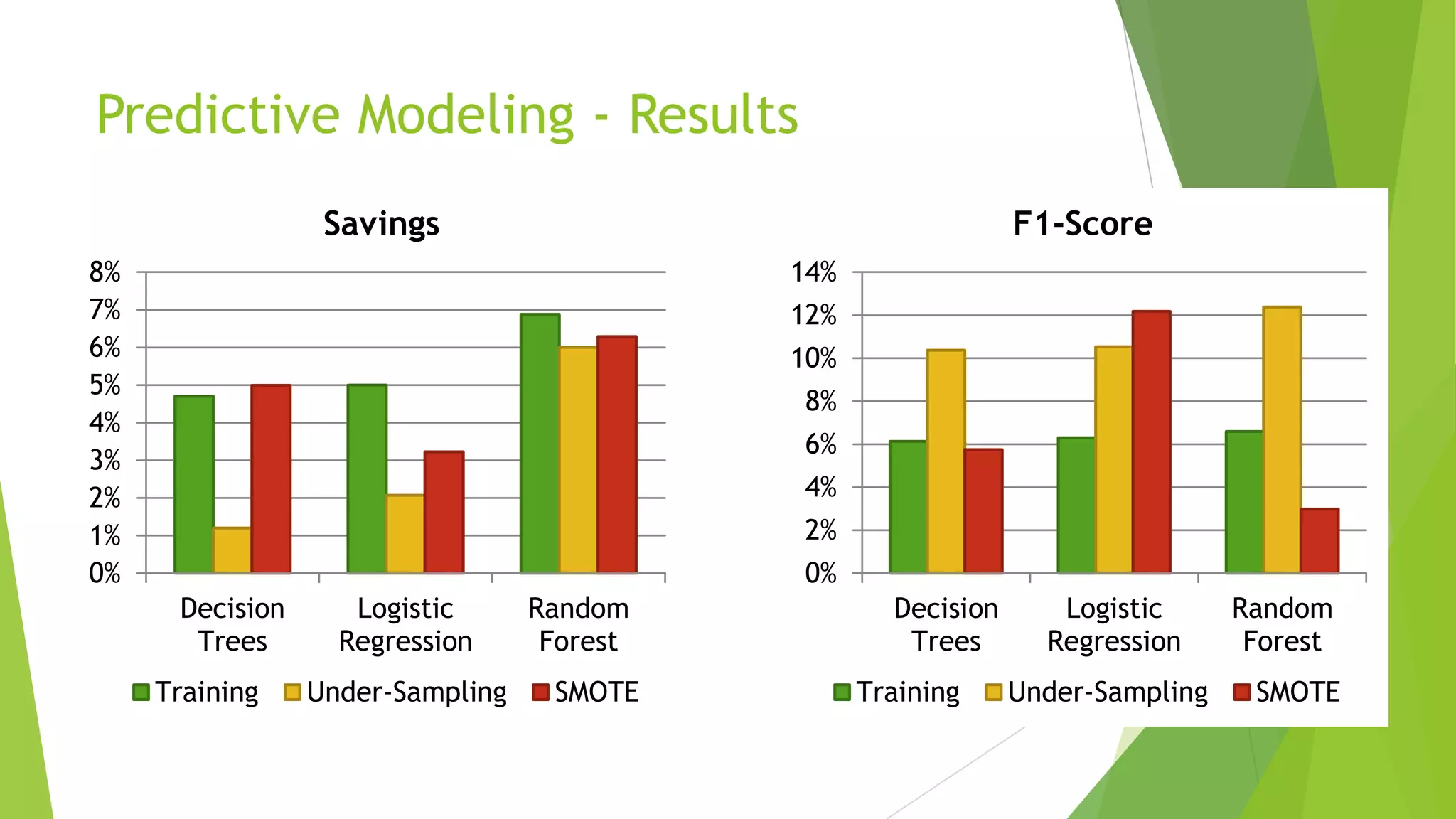
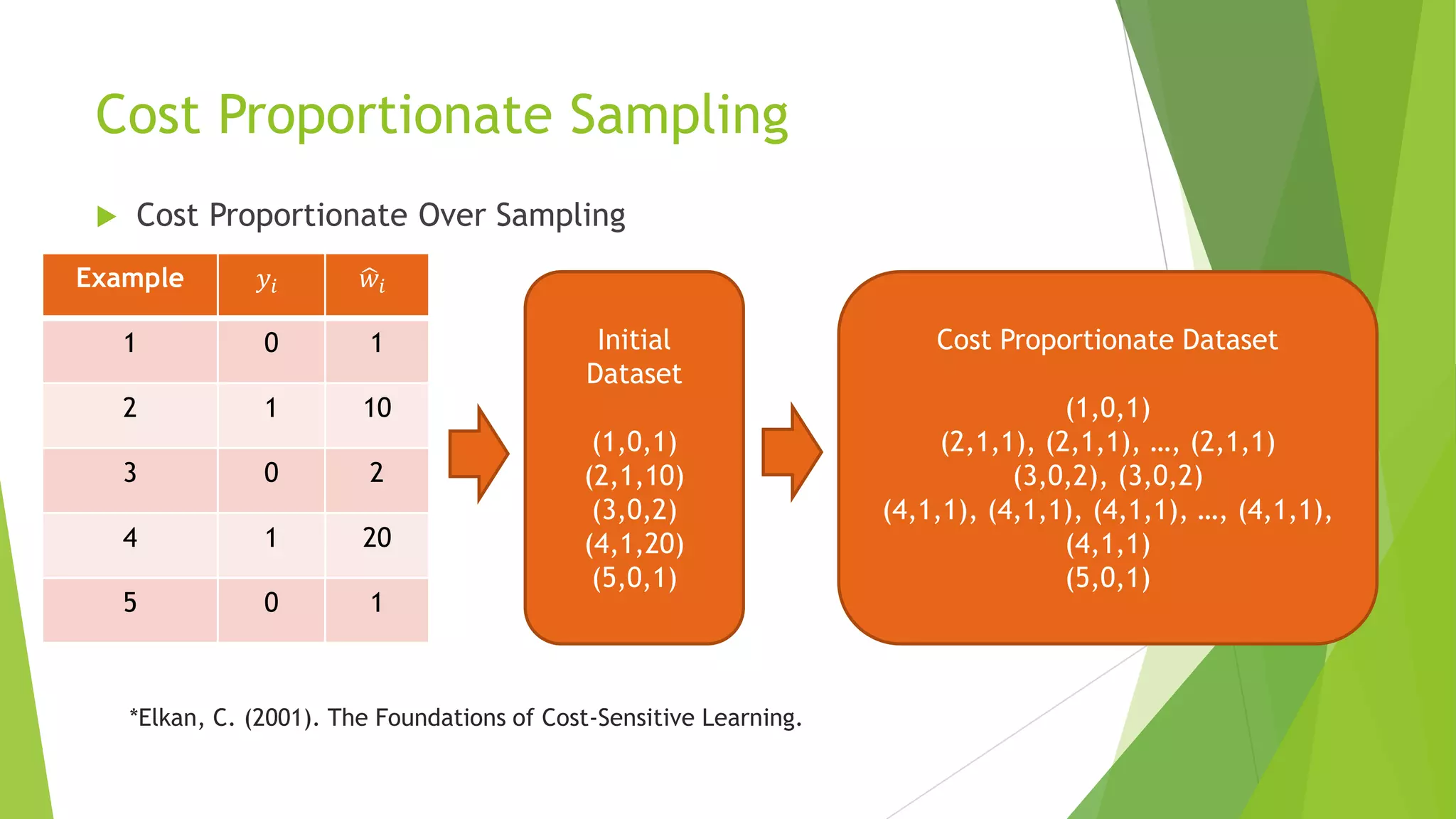
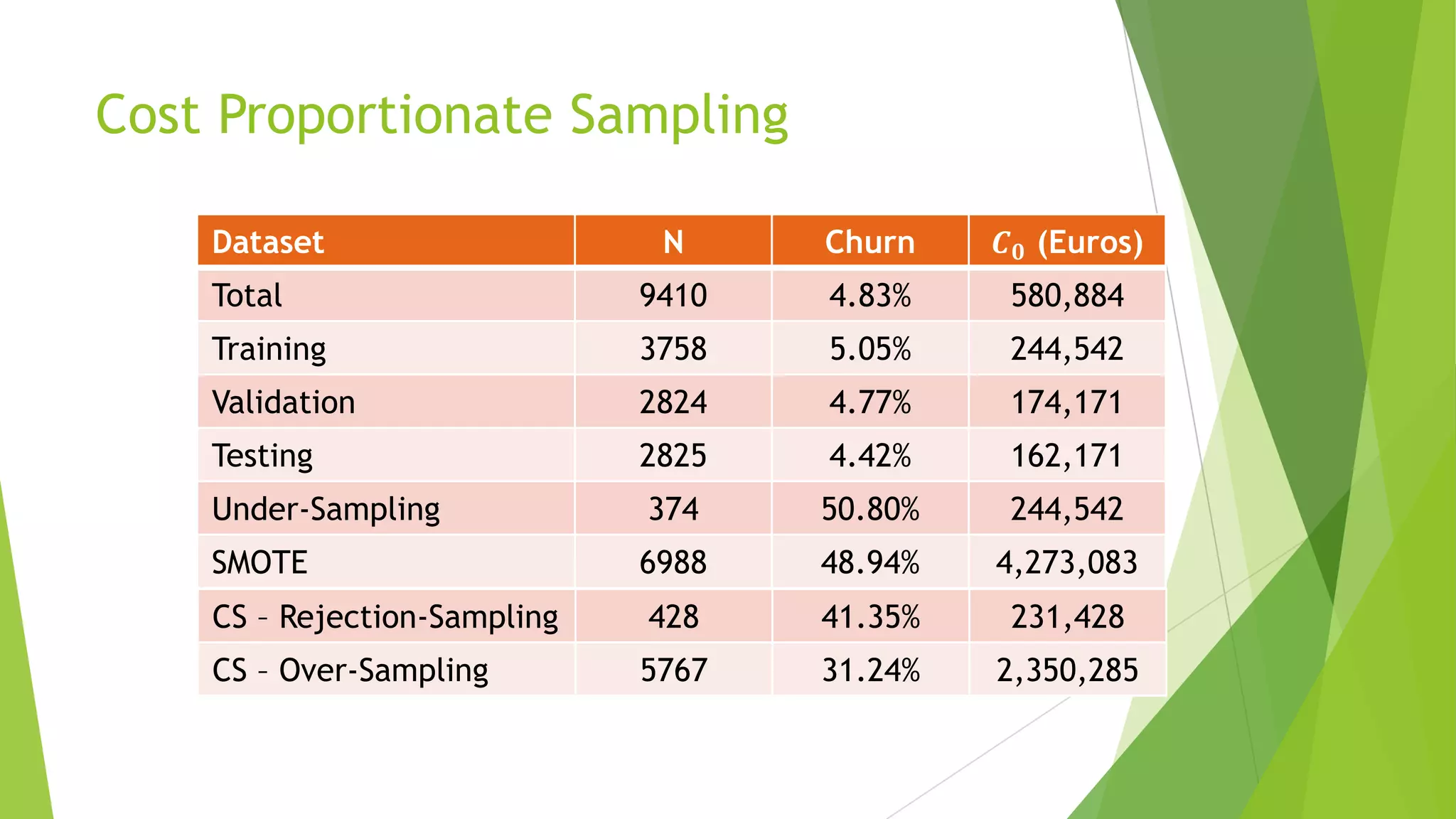
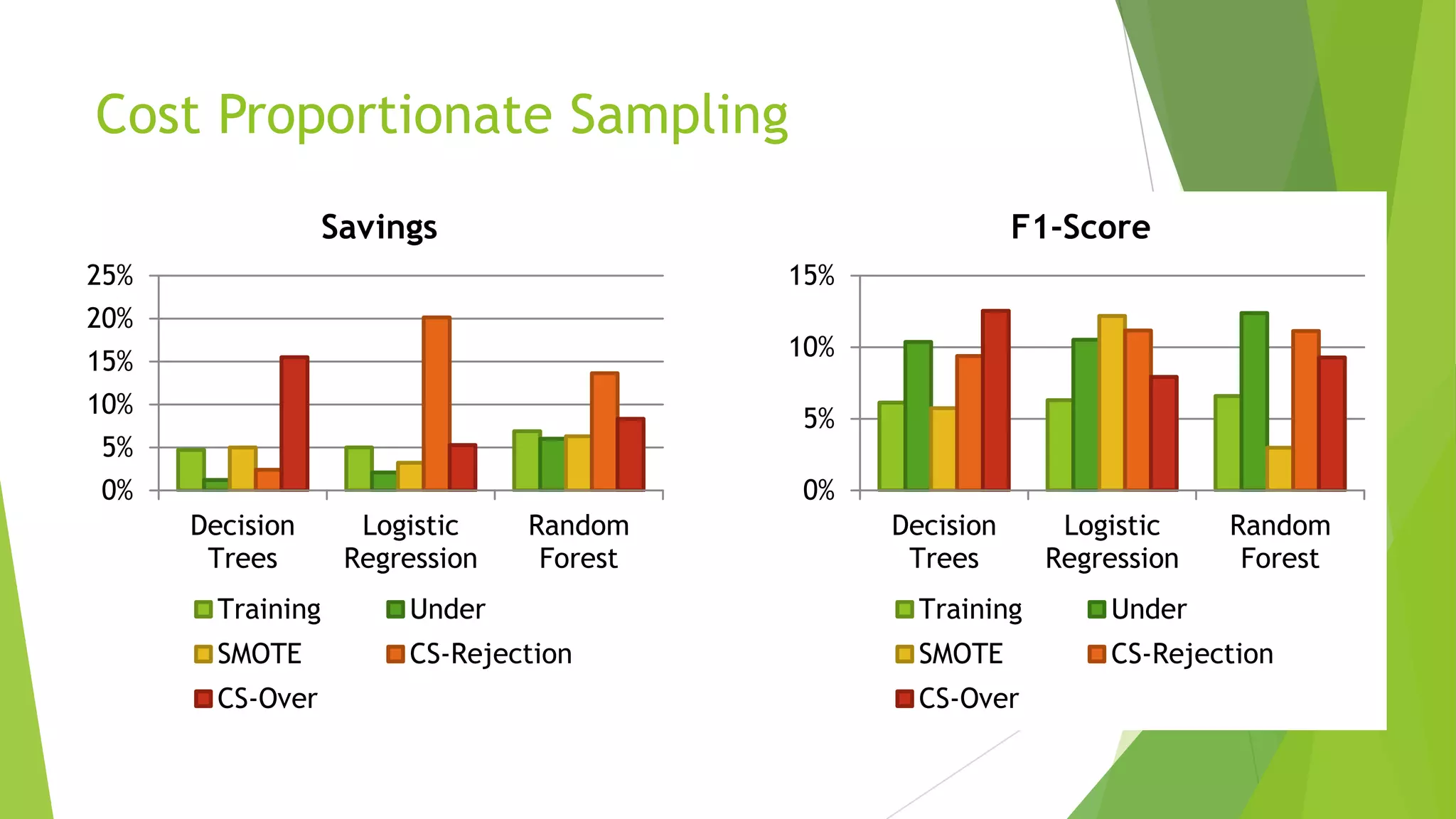
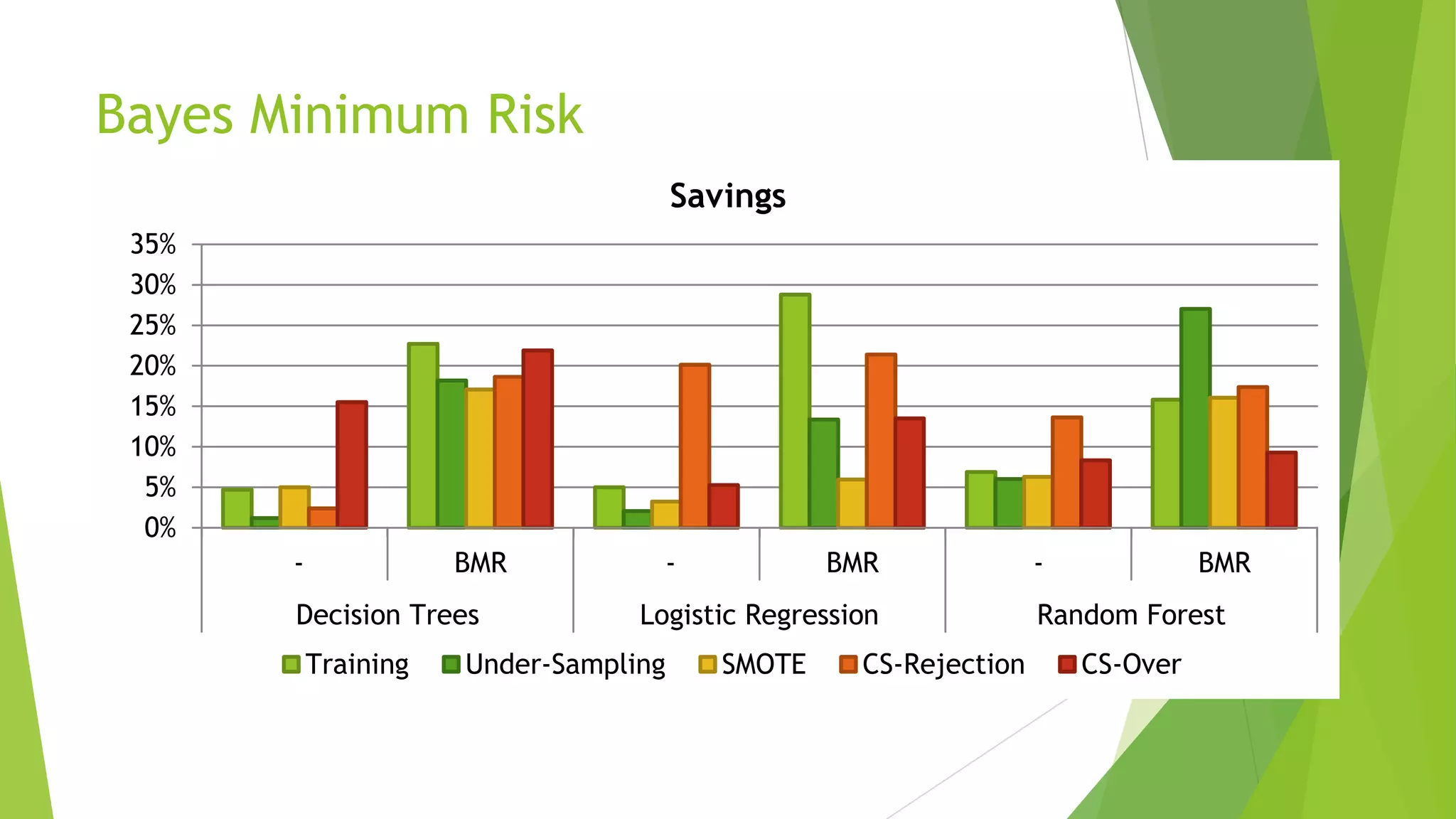
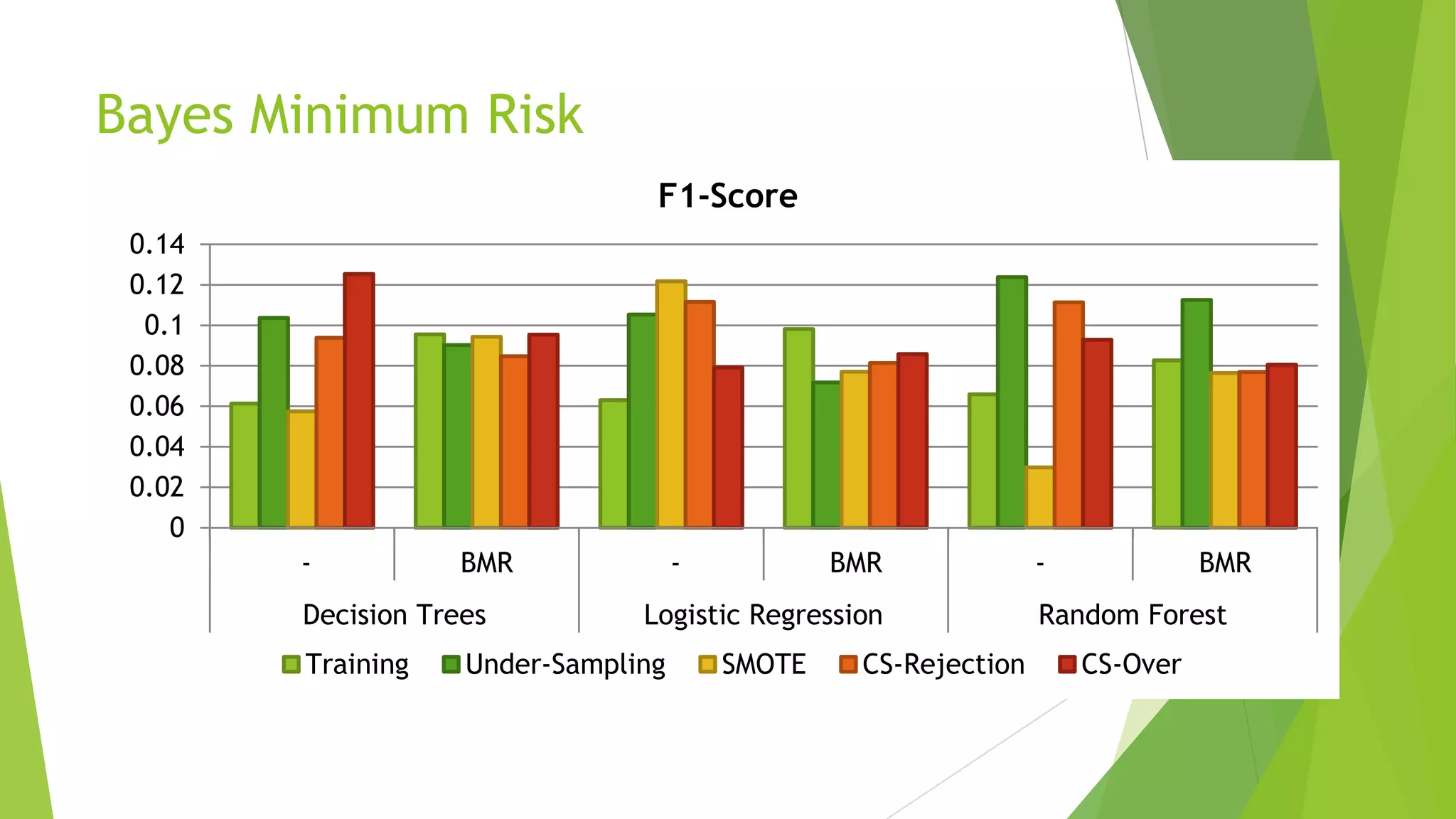
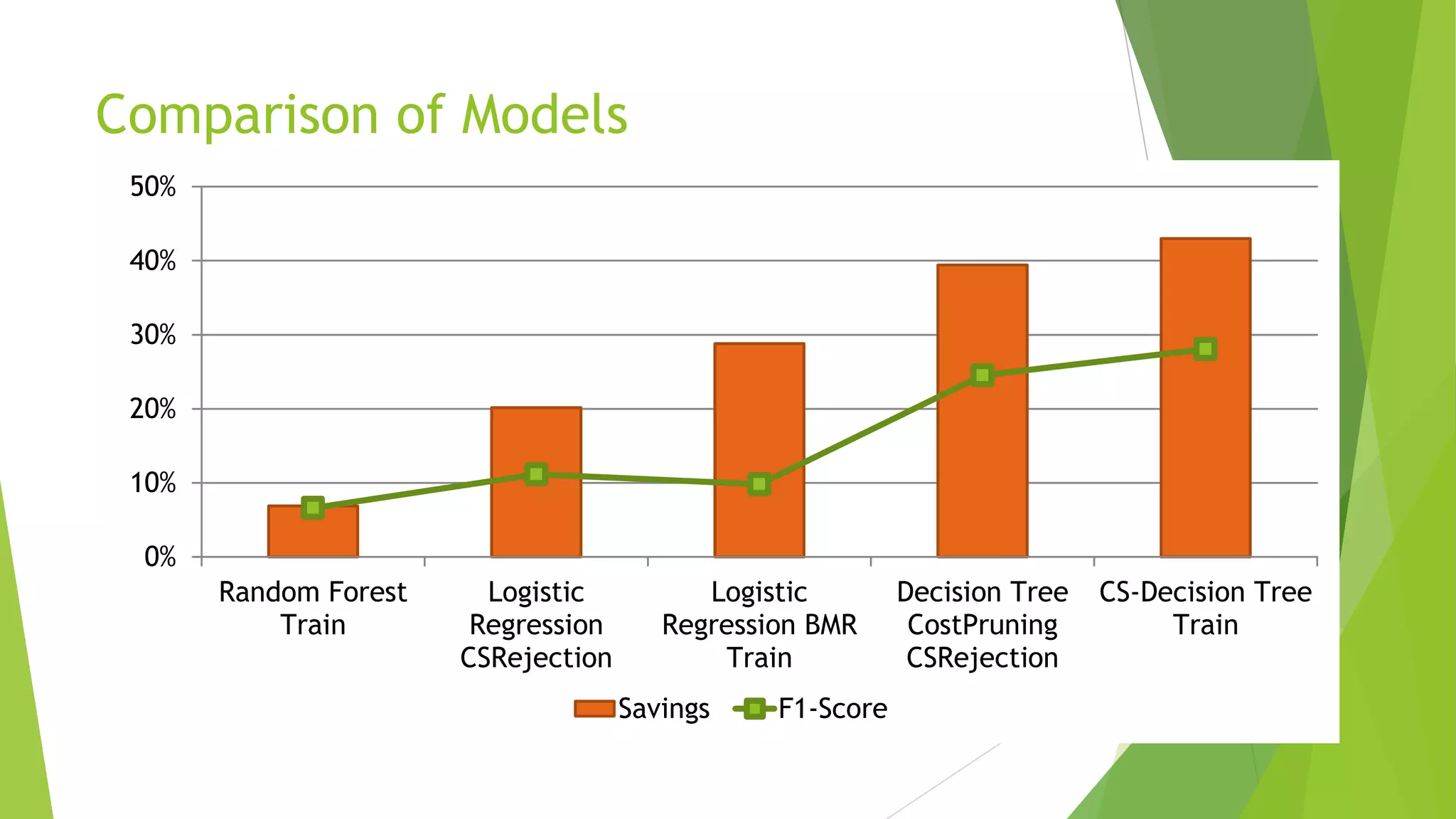
This document summarizes a presentation on maximizing profit from customer churn prediction models using cost-sensitive machine learning techniques. It discusses how traditional evaluation measures like accuracy do not account for different costs of prediction errors. It then covers cost-sensitive approaches like cost-proportionate sampling, Bayes minimum risk, and cost-sensitive decision trees. The results show these cost-sensitive methods improve savings over traditional models and sampling approaches when the business costs are incorporated into the predictive modeling.
More Related Content
Similar to Maximizing a churn campaigns profitability with cost sensitive machine learning
![[DSC Europe 25] Uros Pesic - The Reality of AI in Marketing.pdf](https://cdn.slidesharecdn.com/ss_thumbnails/rtkodnmtycovsllvzsyn-9-251215095918-b0c6bfe3-thumbnail.jpg?width=640&height=640&fit=bounds)
![[DSC Europe 25] Jon Dajci - Bridging TradFi and DeFi: Building the Future of ...](https://cdn.slidesharecdn.com/ss_thumbnails/fqmhfvlbqhkihjvqvhmu-7-251211083849-6af7e325-thumbnail.jpg?width=640&height=640&fit=bounds)
![[DSC Europe 25] Bassam Maharmeh - Artificial Intelligence: Opportunities and ...](https://cdn.slidesharecdn.com/ss_thumbnails/thhfmr2fqpawzj7hsjpg-5-251211083048-2c23204f-thumbnail.jpg?width=640&height=640&fit=bounds)
![[DSC Europe 25] Danica Soc - The Science Behind Marketing: Experimentation me...](https://cdn.slidesharecdn.com/ss_thumbnails/c0nofsggs9gw5ucmallr-3-251216103155-56bd64d1-thumbnail.jpg?width=640&height=640&fit=bounds)
![[DSC Europe 25] Behzad Hosseini - AI Agents in the Wild: Deploying Models tha...](https://cdn.slidesharecdn.com/ss_thumbnails/3qtejajvsjqrzwfept2c-10-251212103250-7f2b1068-thumbnail.jpg?width=640&height=640&fit=bounds)
Maximizing a churn campaigns profitability with cost sensitive machine learning
- 1. Maximizing a churn campaign’sprofitability with cost sensitive machine learning Alejandro Correa Bahnsen, PhD Chief Data Scientist | Easy Solutions Agosto 25 y 26 | Lima – Perú 2017 #BIGDATASUMMIT2017
- 2. Agenda Churn modeling Evaluation Measures Offers Predictive modeling Cost-Sensitive Predictive Modeling Cost Proportionate Sampling Bayes Minimum Risk CS – Decision Trees Conclusions
- 3. Churn Modeling • Detectwhich customers are likely to abandon Voluntary churn Involuntary churn
- 4. Customer Churn ManagementCampaign Inflow New Customers Customer Base Active Customers *Verbraken et. al (2013). A novel profit maximizing metric for measuring classification performance of customer churn prediction models. Predicted Churners Predicted Non-Churners TP: Actual Churners FP: Actual Non-Churners FN: Actual Churners TN: Actual Non-Churners Outflow Effective Churners Churn Model Prediction 1 1 1 − 𝛾𝛾 1
- 5. Evaluation of aCampaign Confusion Matrix • Accuracy = 𝑇𝑃+𝑇𝑁 𝑇𝑃+𝑇𝑁+𝐹𝑃+𝐹𝑁 • Recall = 𝑇𝑃 𝑇𝑃+𝐹𝑁 • Precision = 𝑇𝑃 𝑇𝑃+𝐹𝑃 • F1-Score = 2 𝑃𝑟𝑒𝑐𝑖𝑠𝑖𝑜𝑛 ∗ 𝑅𝑒𝑐𝑎𝑙𝑙 𝑃𝑟𝑒𝑐𝑖𝑠𝑖𝑜𝑛+𝑅𝑒𝑐𝑎𝑙𝑙 True Class (𝑦𝑖) Churner (𝑦𝑖=1) Non- Churner(𝑦𝑖=0) Predicted class (𝑐𝑖) Churner (𝑐𝑖=1) TP FP Non-Churner (𝑐𝑖=0) FN TN
- 6. Evaluation of aCampaign However these measures assign the same weight to different errors Not the case in a Churn model since Failing to predict a churner carries a different cost than wrongly predicting a non-churner Churners have different financial impact
- 7. Financial Evaluation ofa Campaign Inflow New Customers Customer Base Active Customers *Verbraken et. al (2013). A novel profit maximizing metric for measuring classification performance of customer churn prediction models. Predicted Churners Predicted Non-Churners TP: Actual Churners FP: Actual Non-Churners FN: Actual Churners TN: Actual Non-Churners Outflow Effective Churners Churn Model Prediction 0 𝐶𝐿𝑉 𝐶𝐿𝑉 + 𝐶 𝑎𝐶 𝑜 + 𝐶 𝑎 𝐶 𝑜 + 𝐶 𝑎
- 8. Financial Evaluation ofa Campaign Cost Matrix where: True Class (𝑦𝑖) Churner (𝑦𝑖=1) Non- Churner(𝑦𝑖=0) Predicte d class (𝑐𝑖) Churner (𝑐𝑖=1) Non-Churner (𝑐𝑖=0) 𝐶 𝑎 = Administrative cost 𝐶𝐿𝑉𝑖 = Client Lifetime Value of customer 𝑖 𝐶𝑜 𝑖 = Cost of the offer made to customer 𝑖 𝛾𝑖 = Probability that customer 𝑖 accepts the offer 𝐶 𝑇𝑃 𝑖 = 𝛾𝑖 𝐶 𝑜 𝑖 + 1 − 𝛾𝑖 𝐶𝐿𝑉𝑖 + 𝐶 𝑎 𝐶 𝐹𝑁 𝑖 = 𝐶𝐿𝑉𝑖 𝐶 𝑇𝑁 𝑖 = 0 𝐶 𝐹𝑃 𝑖 = 𝐶 𝑜 𝑖 + 𝐶 𝑎
- 9. Financial Evaluation ofa Campaign Using the cost matrix the total cost is calculated as: 𝐶 = 𝑦𝑖 𝑐𝑖 ∙ 𝐶 𝑇𝑃 𝑖 + 1 − 𝑐𝑖 𝐶 𝐹𝑁 𝑖 + 1 − 𝑦𝑖 𝑐𝑖 ∙ 𝐶 𝐹𝑃 𝑖 + 1 − 𝑐𝑖 𝐶 𝑇𝑁 𝑖 Additionally the savings are defined as: 𝐶𝑠 = 𝐶0 − 𝐶 𝐶0 where 𝐶0 is the cost when all the customers are predicted as non-churners
- 10. Financial Evaluation ofa Campaign Customer Lifetime Value *Glady et al. (2009). Modeling churn using customer lifetime value.
- 11. Offers Same offermay not apply to all customers (eg. Already have premium channels) An offer should be made such that it maximizes the probability of acceptance (𝛾)
- 12.
- 13. Offers Analysis 88% 90% 92% 94% 96% 98% 100% 0.0% 1.0% 2.0% 3.0% 4.0% 5.0% 6.0% Cluster 1Cluster 2 Cluster 3 Cluster 4 Churn Rate Gamma (right axis) 𝛾 = Probability that a customer accepts the offer
- 14. Predictive Modeling Dataset NChurn 𝑪 𝟎 (Euros) Total 9410 4.83% 580,884 Training 3758 5.05% 244,542 Validation 2824 4.77% 174,171 Testing 2825 4.42% 162,171 SMOTE 6988 48.94% 4,273,083 Under-Sampling 374 50.80% 244,542
- 15. Predictive Modeling Algorithms Decision Trees Logistic Regression Random Forest
- 16. Predictive Modeling -Results 0% 2% 4% 6% 8% 10% 12% 14% Decision Trees Logistic Regression Random Forest F1-Score Training Under-Sampling SMOTE 0% 1% 2% 3% 4% 5% 6% 7% 8% Decision Trees Logistic Regression Random Forest Savings Training Under-Sampling SMOTE
- 17. Predictive Modeling Samplingtechniques helps to improve models’ predictive power however not necessarily the savings There is a need for methods that aim to increase savings
- 18. Agenda Churn modeling Evaluation Measures Offers Predictive modeling Cost-Sensitive Predictive Modeling Cost Proportionate Sampling Bayes Minimum Risk CS – Decision Trees Conclusions
- 19. Cost-Sensitive Predictive Modeling Traditional methods assume the same cost for different errors Not the case in Churn modeling Some cost-sensitive methods assume a constant cost difference between errors Example-Dependent Cost-Sensitive Predictive Modeling
- 20. Cost-Sensitive Predictive Modeling Changing class distribution Cost Proportionate Rejection Sampling Cost Proportionate Over Sampling Direct Cost Bayes Minimum Risk Modifying a learning algorithm CS – Decision Tree
- 21. Cost Proportionate Sampling Cost Proportionate Over Sampling Example 𝑦𝑖 𝑤𝑖 1 0 1 2 1 10 3 0 2 4 1 20 5 0 1 Initial Dataset (1,0,1) (2,1,10) (3,0,2) (4,1,20) (5,0,1) Cost Proportionate Dataset (1,0,1) (2,1,1), (2,1,1), …, (2,1,1) (3,0,2), (3,0,2) (4,1,1), (4,1,1), (4,1,1), …, (4,1,1), (4,1,1) (5,0,1) *Elkan, C. (2001). The Foundations of Cost-Sensitive Learning.
- 22. 𝑤𝑖/max( 𝑤𝑖) 0.05 0.5 0.1 1 0.05 Cost ProportionateSampling Cost Proportionate Rejection Sampling Example 𝑦𝑖 𝑤𝑖 1 0 1 2 1 10 3 0 2 4 1 20 5 0 1 Initial Dataset (1,0,1) (2,1,10) (3,0,2) (4,1,20) (5,0,1) Cost Proportionat e Dataset (2,1,1) (4,1,1) (4,1,1) (5,0,1) *Zadrozny et al. (2003). Cost-sensitive learning by cost-proportionate example weighting.
- 23. Cost Proportionate Sampling DatasetN Churn 𝑪 𝟎 (Euros) Total 9410 4.83% 580,884 Training 3758 5.05% 244,542 Validation 2824 4.77% 174,171 Testing 2825 4.42% 162,171 Under-Sampling 374 50.80% 244,542 SMOTE 6988 48.94% 4,273,083 CS – Rejection-Sampling 428 41.35% 231,428 CS – Over-Sampling 5767 31.24% 2,350,285
- 24. Cost Proportionate Sampling 0% 5% 10% 15% 20% 25% Decision Trees Logistic Regression Random Forest Savings TrainingUnder SMOTE CS-Rejection CS-Over 0% 5% 10% 15% Decision Trees Logistic Regression Random Forest F1-Score Training Under SMOTE CS-Rejection CS-Over
- 25. Bayes Minimum Risk Decision model based on quantifying tradeoffs between various decisions using probabilities and the costs that accompany such decisions Risk of classification 𝑅 𝑐𝑖 = 0|𝑥𝑖 = 𝐶 𝑇𝑁 𝑖 1 − 𝑝𝑖 + 𝐶 𝐹𝑁 𝑖 ∙ 𝑝𝑖 𝑅 𝑐𝑖 = 1|𝑥𝑖 = 𝐶 𝐹𝑃 𝑖 1 − 𝑝𝑖 + 𝐶 𝑇𝑃 𝑖 ∙ 𝑝𝑖 Using the different risks the prediction is made based on the following condition: 𝑐𝑖 = 0 𝑅 𝑐𝑖 = 0|𝑥𝑖 ≤ 𝑅 𝑐𝑖 = 1|𝑥𝑖 1 𝑜𝑡ℎ𝑒𝑟𝑤𝑖𝑠𝑒
- 26. Bayes Minimum Risk 0% 5% 10% 15% 20% 25% 30% 35% -BMR - BMR - BMR Decision Trees Logistic Regression Random Forest Savings Training Under-Sampling SMOTE CS-Rejection CS-Over
- 27. Bayes Minimum Risk 0 0.02 0.04 0.06 0.08 0.1 0.12 0.14 -BMR - BMR - BMR Decision Trees Logistic Regression Random Forest F1-Score Training Under-Sampling SMOTE CS-Rejection CS-Over
- 28. Bayes Minimum Risk Bayes Minimum Risk increases the savings by using a cost- insensitive method and then introducing the costs Why not introduce the costs during the estimation of the methods?
- 29. CS – DecisionTrees Decision trees Classification model that iteratively creates binary decision rules 𝑥 𝑗, 𝑙 𝑗 𝑚 that maximize certain criteria Where 𝑥 𝑗, 𝑙 𝑗 𝑚 refers to making a rule using feature 𝑗 on value 𝑚
- 30. Comparison of Models 0% 10% 20% 30% 40% 50% RandomForest Train Logistic Regression CSRejection Logistic Regression BMR Train Decision Tree CostPruning CSRejection CS-Decision Tree Train Savings F1-Score
- 31. Conclusions Selecting modelsbased on traditional statistics does not gives the best results measured by savings Incorporating the costs into the modeling helps to achieve higher savings
- 33. Thank you! Alejandro CorreaBahnsen acorrea@easysol.net