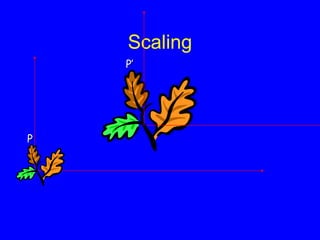
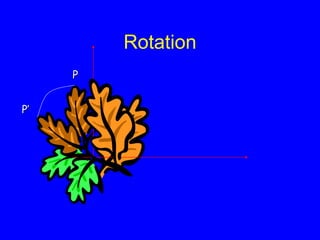
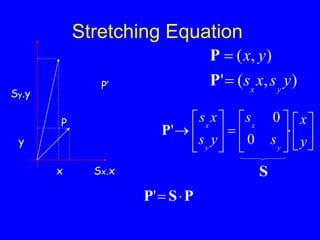
This document provides an introduction to Matlab and a review of linear algebra concepts. It discusses starting Matlab, getting help, vectors, matrices, common operations, and linear transformations including translation, scaling, rotation, and affine transformations. Examples are provided for how to represent and perform these transformations using Matlab code and matrix mathematics. The document concludes by mentioning files, functions, images, and debugging in Matlab.

1. Matlab tutorial and Linear
Algebra Review
• Today’s goals:
• Learn enough matlab to get started.
• Review some basics of Linear Algebra
• Essential for geometry of points and lines.
• But also, all math is linear algebra.
• (ok slight exaggeration).
• Many slides today adapted from Octavia
Camps, Penn State.

2. Starting Matlab
• For PCs, Matlab should be a program.
• For Sun’s:
Numerical
Analysis and Visualization
Matlab 6.1

3. Help
• help
• help command
Eg., help plus
• Help on toolbar
• demo
• Tutorial:
http://amath.colorado.edu/scico/tutorials
/matlab/

4. Matlab interpreter
• Many common functions: see help ops

5. Vectors
• Ordered set of
numbers: (1,2,3,4)
• Example: (x,y,z)
coordinates of pt in
space. r
unit vecto
a
is
,
1
If
)
,
(
1
2
,
,
2
1
v
v
x
v
x
x
x
v
n
i i
n







6. Indexing into vectors

7. Vector Addition
)
,
(
)
,
(
)
,
( 2
2
1
1
2
1
2
1 y
x
y
x
y
y
x
x 




w
v
v
w
V+w

8. Scalar Product
)
,
(
)
,
( 2
1
2
1 ax
ax
x
x
a
a 

v
v
av

9. Operations on vectors
• sum
• max, min, mean, sort, …
• Pointwise: .^

10. Inner (dot) Product
v
w

2
2
1
1
2
1
2
1 .
)
,
).(
,
(
. y
x
y
x
y
y
x
x
w
v 


The inner product is a SCALAR!

cos
||
||
||
||
)
,
).(
,
(
. 2
1
2
1 w
v
y
y
x
x
w
v 


w
v
w
v 

 0
.

11. Matrices


















nm
n
n
m
m
m
m
n
a
a
a
a
a
a
a
a
a
a
a
a
A








2
1
3
32
31
2
22
21
1
12
11
m
n
m
n
m
n B
A
C 

 

Sum:
ij
ij
ij b
a
c 

A and B must have the same
dimensions

12. Matrices
p
m
m
n
p
n B
A
C 

 
Product:



m
k
kj
ik
ij b
a
c
1
A and B must have
compatible dimensions
n
n
n
n
n
n
n
n A
B
B
A 


 
Identity Matrix:
A
AI
IA
I 
















1
0
0
0
1
0
0
0
1








13. Matrices
m
n
T
n
m A
C 
 
Transpose:
ji
ij a
c  T
T
T
A
B
AB 
)
(
T
T
T
B
A
B
A 

 )
(
If A
AT
 A is symmetric

14. Matrices
Determinant: A must be square
32
31
22
21
13
33
31
23
21
12
33
32
23
22
11
33
32
31
23
22
21
13
12
11
det
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a













12
21
22
11
22
21
12
11
22
21
12
11
det a
a
a
a
a
a
a
a
a
a
a
a










15. Matrices
I
A
A
A
A n
n
n
n
n
n
n
n 
 





1
1
Inverse: A must be square

















11
21
12
22
12
21
22
11
1
22
21
12
11 1
a
a
a
a
a
a
a
a
a
a
a
a

16. Indexing into matrices

17. Euclidean transformations

18. 2D Translation
t
P
P’

19. 2D Translation Equation
P
x
y
tx
ty
P’
t
t
P
P 



 )
,
(
' y
x t
y
t
x
)
,
(
)
,
(
y
x t
t
y
x


t
P

20. 2D Translation using Matrices
P
x
y
tx
ty
P’
t
)
,
(
)
,
(
y
x t
t
y
x


t
P



























1
1
0
0
1
' y
x
t
t
t
y
t
x
y
x
y
x
P
t P

21. Scaling
P
P’

22. Scaling Equation
P
x
y
s.x
P’
s.y
)
,
(
'
)
,
(
sy
sx
y
x


P
P
P
P 
 s
'





















y
x
s
s
sy
sx
0
0
'
P
S
P
S
P 

'

23. Rotation
P
P’

24. Rotation Equations
Counter-clockwise rotation by an angle 











 







y
x
y
x




cos
sin
sin
cos
'
'
P
x
Y’
P’

X’
y R.P
P'

25. Degrees of Freedom
R is 2x2 4 elements
BUT! There is only 1 degree of freedom: 
1
)
det( 




R
I
R
R
R
R T
T
The 4 elements must satisfy the following constraints:











 







y
x
y
x




cos
sin
sin
cos
'
'

26. Stretching Equation
P
x
y
Sx.x
P’
Sy.y





















y
x
s
s
y
s
x
s
y
x
y
x
0
0
'
P
)
,
(
'
)
,
(
y
s
x
s
y
x
y
x


P
P
S
P
S
P 

'

27. Stretching = tilting and projecting
(with weak perspective)







































y
x
s
s
s
y
x
s
s
y
s
x
s
y
x
y
y
x
y
x
1
0
0
0
0
'
P

28. Linear Transformation










































































y
x
s
s
s
y
x
s
s
y
x
d
c
b
a
y
x
y
y
x
















sin
cos
cos
sin
1
0
0
sin
cos
cos
sin
sin
cos
cos
sin
0
0
sin
cos
cos
sin
'
P
SVD

29. Affine Transformation


















1
' y
x
ty
d
c
tx
b
a
P

30. Files

31. Functions
• Format: function o = test(x,y)
• Name function and file the same.
• Only first function in file is visible
outside the file.

32. Images

33. Debugging
• Add print statements to function by
leaving off ;
• keyboard
• debug and breakpoint

34. Conclusions
• Quick tour of matlab, you should teach
yourself the rest. We’ll give hints in
problem sets.
• Linear algebra allows geometric
manipulation of points.
• Learn to love SVD.