This document is an educational resource from the University of M'Hamed Bougara focusing on matrix computations and linear algebra in MATLAB. It covers fundamental topics such as matrix generation, manipulation, operations, solving linear equations, and working with polynomials represented by vectors. The document provides guidance on using MATLAB commands and functions to perform matrix-related tasks efficiently.

1. University of M’hamed BOUGARA of Boumerdes
Institute of Electrical and Electronics Engineering
(IGEE ex-INELEC)
Department of Power and Control engineering
Chapter 1: Matrix computations and linear algebra.
Dr. A. AMMAR
EE421 – Computation and Simulation using MATLAB /Simulink
12/10/2024 EE421 Dr. AMMAR 1

2. 12/10/2024 EE421 Dr. AMMAR 2
Chapter 1: Matrix computations and linear algebra.
Matrices are the basic elements of the MATLAB environment. A matrix is a two-
dimensional array consisting of m rows and n columns. Special cases are
column vectors (n = 1) and row vectors (m = 1).
In this section we will illustrate how to apply different operations on matrices,
the inverse of a matrix, determinants, and matrix manipulation.
1 Matrix generation
Matrices are fundamental to MATLAB. Therefore, we need to become familiar
with matrix generation and manipulation. Matrices can be generated in several
ways.

3. 12/10/2024 EE421 Dr. AMMAR 3
1.1. Entering a vector
A vector is a special case of a matrix. an array of dimension 1 × n is called a row
vector, whereas an array of dimension m × 1 is called a column vector
The elements of vectors in MATLAB are enclosed by square brackets and are
separated by spaces or by commas. For example, to enter a row vector, v, type
Column vectors are created in a similar way, however, semicolon (;) must separate
the components of a column vector,

4. 12/10/2024 EE421 Dr. AMMAR 4
On the other hand, a row vector is converted to a column vector using the
transpose operator. The transpose operation is denoted by an apostrophe (’).
Thus, w(1) is the first element of vector w, w(2) its second element, and so forth.
Furthermore, to access blocks of elements, we use MATLAB’s colon operator (:).
For example, to access the first three elements of W, we write,

5. 12/10/2024 EE421 Dr. AMMAR 5
Or, all elements from the third through the last elements,
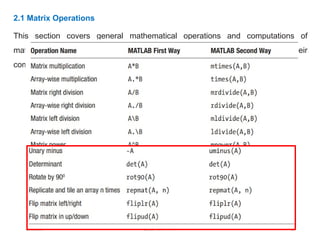
1.2 Entering a matrix
A matrix is an array of numbers. To type a matrix into MATLAB you must:
• begin with a square bracket, [
• separate elements in a row with spaces or commas (,)
• use a semicolon (;) to separate rows
• end the matrix with another square bracket, ]
For example to enter a matrix A,

6. 12/10/2024 EE421 Dr. AMMAR 6
Once we have entered the matrix, it is automatically stored and remembered in the
Workspace. We can refer to it simply as matrix A. We can then view a particular
element in a matrix by specifying its location. We write,

7. 12/10/2024 EE421 Dr. AMMAR 7
1.3 Matrix generators
MATLAB provides functions that generates elementary matrices. The matrix of
zeros, the matrix of ones, and the identity matrix are returned by the functions
zeros, ones, and eye, respectively (Table.1).
Examples

8. 12/10/2024 EE421 Dr. AMMAR 8
1.4 Special matrices
MATLAB provides a number of special matrices (see Table 2.5). These matrices
have interesting properties that make them useful for constructing examples and
for testing algorithms (Table.2).

9. 12/10/2024 EE421 Dr. AMMAR 9
Examples
2. Matrix manipulation and operation
The MATLAB command for the determinant computation is det().

10. 12/10/2024 EE421 Dr. AMMAR 10
The MATLAB command for the transpose operation is transpose(), ‘ .
For example:
The MATLAB command to compute the inverse of a matrix is inv(). For example,

11. 12/10/2024 EE421 Dr. AMMAR 11
2.1 Matrix Operations
This section covers general mathematical operations and computations of
matrices, vectors, and eigenvectors. Table.3 lists the matrix operations their
command syntax.

12. 12/10/2024 EE421 Dr. AMMAR 12
Examples
Note the difference between .^ and ^

13. 12/10/2024 EE421 Dr. AMMAR 13
Example:
Performing Matrix Operations
Let’s perform some matrix operations—such as summation, subtraction,
multiplication, power, scalar multiplication, square root, mean, round, standard
deviations, and replicate/rotate/flip matrix—from the Command Window.

14. 12/10/2024 EE421 Dr. AMMAR 14

15. 12/10/2024 EE421 Dr. AMMAR 15
2.2 Other Matrices manipulations
We select elements in a matrix just as we did for vectors, but now we need two
indices. The element of row i and column j of the matrix A is denoted by A(i,j). Thus,
A(i,j) in MATLAB refers to the element Aij of matrix A. The first index is the row
number and the second index is the column number. For example, A(1,3) is an
element of first row and third column. Here, A(1,3)=3
Correcting any entry is easy through indexing.
Here we substitute A(3,3)=9 by A(3,3)=0.
The result is

16. 12/10/2024 EE421 Dr. AMMAR 16
Creating a sub-matrix
To extract a submatrix B consisting of rows 2 and 3 and columns 1 and 2 of the matrix
A, do the following:
To interchange rows 1 and 2 of A, use the vector of row indices together with the
colon operator.

17. 12/10/2024 EE421 Dr. AMMAR 17
To delete a row or column of a matrix, use the empty vector operator, [ ].
To determine the dimensions of a matrix or vector, use the command size. For
example
Colon operator in a matrix
The colon operator can also be used to pick out a certain row or column. For
example, the statement A(m:n,k:l specifies rows m to n and column k to l.
Subscript expressions refer to portions of a matrix.

18. 12/10/2024 EE421 Dr. AMMAR 18
For example
Is the second row elements of A.
The colon operator can also be used to extract a sub-matrix from a matrix A.
A(:,2:3) is a sub-matrix with the last two columns of A.
• A(:,j) is the jth
column of A,
• A(i,:) is the ith
row,
• A(end,:) picks out the last row of A

19. 12/10/2024 EE421 Dr. AMMAR 19
The keyword end, used in A(end,:), denotes the last index in the specified dimension.
Here are some examples
2.3 Eigen-Values
eig () produces a column vector E containing the eigenvalues of a square
matrix A.
>> A=([2.3, 3.4, 5; 3, 2.4, -1.5; 2, -0.4, -7.2])
A =
2.3000 3.4000 5.0000
3.0000 2.4000 -1.5000
2.0000 -0.4000 -7.2000
>> eig(A)
ans =
5.7726
0.1619
-8.4345

20. 12/10/2024 EE421 Dr. AMMAR 20

21. 12/10/2024 EE421 Dr. AMMAR 21
3 Solving linear equations
One of the problems encountered most frequently in scientific computation is the
solution of systems of simultaneous linear equations. With matrix notation, a system
of simultaneous linear equations is written
Ax = b
A is a given square matrix of order n, b is a given column vector of n components,
and x is an unknown column vector of n components
In linear algebra we learn that the solution to Ax = b can be written as x = A-1
b,
where A-1
is the inverse of A
For example, consider the following system of linear equations

22. 12/10/2024 EE421 Dr. AMMAR 22
The coefficient matrix A is and the vector
There are typically two ways to solve for x in MATLAB
1. The first one is to use the matrix inverse, inv
2. The second one is to use the backslash ()operator. The numerical algorithm
behind this operator is computationally efficient. This is a numerically reliable way
of solving system of linear equations by using a well-known process of Gaussian
elimination.

23. 12/10/2024 EE421 Dr. AMMAR 23
the backslash operator, which solves the system of linear equations directly. It’s
based on the Gaussian elimination method.
There are a number of operators and built-in functions in MATLAB that can be used
to solve a linear system of equations. They are as follows:
• mldivide(), which is a built-in function similar to the backslash operator.
• linsolve(), which is is a built-in function similar to the backslash operator.
• lsqr(), which is a built-in function based on the Least Squares Method.
• lu(), which is a built-in function based on the Gauss Elimination Method

24. 12/10/2024 EE421 Dr. AMMAR 24
4. Polynomials Represented by Vectors
Polynomials are represented via vectors using coefficients of polynomials in
descending order. For instance, a fifth order polynomial is given by:
That is defined as a vector space in the following manner:
Note, that MATLAB reads vector entries as a vector of length n+1 as an n-th order
polynomial. Thus, if any of the given polynomial misses any coefficients, zero has
to be entered for its coefficient. For instance, in the previous example, 0 is entered
for the coefficient of x3
.

25. 12/10/2024 EE421 Dr. AMMAR 25
To compute the roots of polynomials, we can use the function roots()

26. 12/10/2024 EE421 Dr. AMMAR 26
5. Ordinary Differential Equations