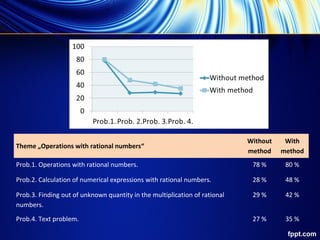
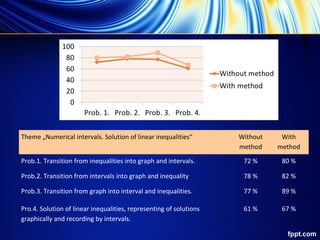
The document discusses methods used to teach mathematics concepts to 5th, 6th, and 7th grade students. Three themes were identified for each grade: defining common multiples and least common multiples, operations with rational numbers, and numerical intervals and linear inequalities. Different interactive methods were presented to students, who then chose one. Results show students performed better on assessments when active learning methods were used compared to traditional instruction without methods. A work meeting found the methods applied led to increased student interest, participation, and skills.

2. For better and interactive learning of the educational
content in Mathematics, the team of teachers has fixed
on three main themes in the grades 5th
, 6th
and 7th
.
Three methods each of the themes have been presented
before the students, giving them an opportunity for
choosing a method.
Results are presented in Tables and Graphs, divided into
two categories: with application of the method and
without application of the method.

3. ThemeTheme: DEFINING OFDEFINING OF CMCM ANDAND LCMLCM
MethodsMethods::
– Differentiated instruction;
– Play methods;
– Flipped classroom.
Method, chosen by the studentsMethod, chosen by the students::
FLLIPPED CLASSROOMFLLIPPED CLASSROOM
55.. GRADEGRADE

4. Prior applying the method
„„FLIPPED CLASSROOMFLIPPED CLASSROOM““
students have learned/acquired the knowledge
independently slower, thus taking them more time.
In the beginning, most of them could not learn their
lessons at home and it was necessary to spare a part
of the lesson time for clarification of the material
misunderstood by them.

5. The method gave them the opportunity to see how
they could distribute the time for fully learning of the
new knowledge outside school and to separate the
significant and important one for the lesson.
It gave them an advantage at the independent
fulfillment of the problems/tasks and projects set for
homework

6. Theme „Common multiple and least common multiple of natural numbers“. Without
method
With
method
Prob.1. Defining of multiple. 71 % 74 %
Prob.2. Finding out of common multiple. 68 % 71 %
Prob.3. Finding out of the least common multiple. 62 % 68 %
Prob.4. Text problem for finding out of Least Common Multiple. 28 % 42 %

7. Theme: OPERATIONS WITH RATIONAL NUMBERSOPERATIONS WITH RATIONAL NUMBERS
Methods:
– Method of the work stations;
– Independent work;
– Cluster (group) method.
Method chosen by the students:
METHOD OF THE WORK STATIONSMETHOD OF THE WORK STATIONS
6.6. GRADEGRADE

8. • Engagement of students and increasing of their activity;
• Increasing of the responsibility of students for the result
of the education;
• Skill to find out ways for elimination of the mistakes
made;
• Development of the creative potential.
Application of the method has led to:

9. Theme „Operations with rational numbers“
Without
method
With
method
Prob.1. Operations with rational numbers. 78 % 80 %
Prob.2. Calculation of numerical expressions with rational numbers. 28 % 48 %
Prob.3. Finding out of unknown quantity in the multiplication of rational
numbers.
29 % 42 %
Prob.4. Text problem. 27 % 35 %

10. Theme: NUMERICAL INTERVALSNUMERICAL INTERVALS.. RECORDING OF THERECORDING OF THE
SOLUTIONS FOR LINEAR INEQUALITIES VIA INTERVALSSOLUTIONS FOR LINEAR INEQUALITIES VIA INTERVALS
Methods:
–– Differentiated instructionDifferentiated instruction
–– I knowI know––I wonderI wonder––I learnI learn
–– Presentation in Maths lessonPresentation in Maths lesson
Method, chosen by students:
I KNOWI KNOW––I WONDERI WONDER––I LEARNI LEARN
7.7. GRADEGRADE

11. – optimizing of the educational process;
– increasing of the share of independent work for the
account of the collective one;
– better rationalizing of the types of numerical intervals
and their application at making visual the solutions of
linear inequalities;
– the interest of students towards Mathematics has
increased.
Application of the method has lead to:

12. Theme „Numerical intervals. Solution of linear inequalities“ Without
method
With
method
Prob.1. Transition from inequalities into graph and intervals. 72 % 80 %
Prob.2. Transition from intervals into graph and inequality 78 % 82 %
Prob.3. Transition from graph into interval and inequalities. 77 % 89 %
Pro.4. Solution of linear inequalities, representing of solutions
graphically and recording by intervals.
61 % 67 %

13. • Increasing of the interest of students at learning the
educational content.
• Students have succeeded in fully participating in the
educational process, each one according to his
capabilities.
• Creation of constructive atmosphere.
• Possibilities and skills for cooperation, planning and
fulfillment of mutual activities have appeared.
At a work meeting, it has been established that theAt a work meeting, it has been established that the
methods applied have led tomethods applied have led to ::

14. • Helps the student to unite the new information with
the one already got.
• Helps students of various styles of studying, to study
more completely.
• Enhances the persistence of students at studying,
enthusiasm of students and confidence in the
teacher.
• Development of self-confidence.
• Increases the level of critical attitude to thinking.
• Increases the competency, life values and improves
the vital crafts.