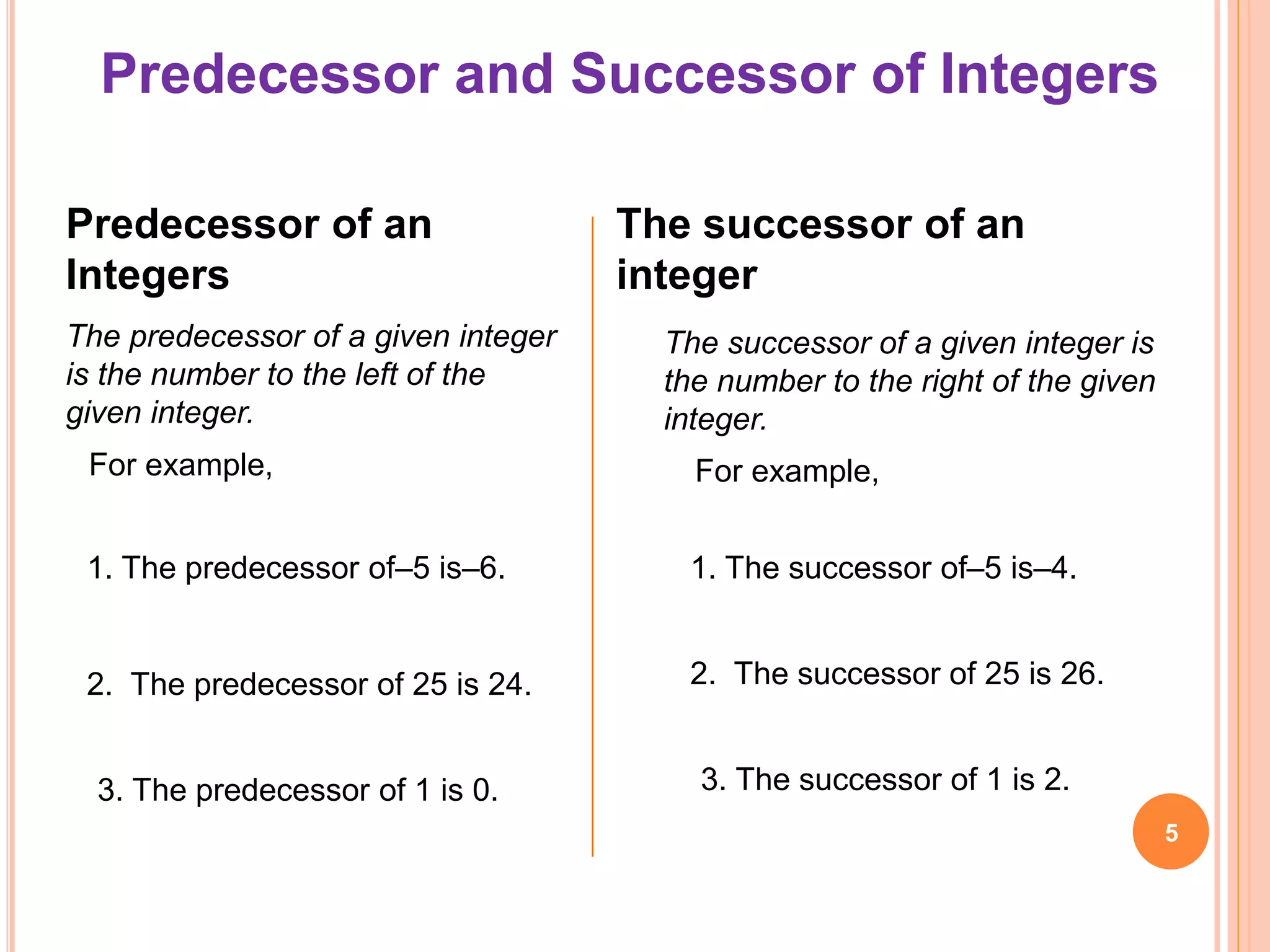
This document provides an overview of integers in mathematics for 7th grade. It discusses representing integers on a number line, comparing integers, and performing addition and subtraction of integers using a number line. Key concepts covered include the properties of addition and subtraction of integers, as well as examples of applying integers in real-life situations such as bank accounts, temperature, and depth measurements. Students are assigned homework problems practicing representing, comparing, and calculating with integers.

1. Subject: Mathematics
Grade: VII
Topic: Integers
1
PPT NO 3

2. Basic Concepts :
1. Natural numbers, whole numbers and integers
2. To represent integers on a number line
3. To compare integers
4. Addition and subtraction of integers
5. The properties of addition and subtraction of integers
Learning Outcomes:
Multiplication and division of integers
The properties of multiplication and division of integers
Application of integers in real life situations
2

3. We often come across situations where we
use directed numbers such as:
• The profit of a company is taken as positive and the loss incurred is taken
as negative.
• Depositing money in a bank account is shown with a positive sign while
withdrawing money from a bank account is shown with a negative sign.
• The altitudes above sea level are taken as positive while the depth
below sea level is taken as negative.
Representation of Integers on the
Number Line
3

4. 4
• Thus, numbers are in the ascending order on the number line.
Ordering of Integers
• On the number line, the numbers increase as we move towards
the right
• On the number line, the numbers decrease as we move towards
left.
• Among the negative integers, the greatest negative integer is –1.
• Zero is greater than every negative integer.
• Every positive integer is greater than every negative integer and zero.
• The smallest positive integer is1.

5. 5
The successor of a given integer is
the number to the right of the given
integer.
Predecessor and Successor of Integers
Predecessor of an
Integers
The predecessor of a given integer
is the number to the left of the
given integer.
For example,
1. The predecessor of–5 is–6.
2. The predecessor of 25 is 24.
3. The predecessor of 1 is 0.
The successor of an
integer
For example,
1. The successor of–5 is–4.
2. The successor of 25 is 26.
3. The successor of 1 is 2.

6. ADDITION AND SUBTRACTION OF INTEGERS
6
Addition of Integers using a Number Line:-
On a number line the plus sign indicates moving to the right while
the minus sign indicates moving to the left.
When two integers of same sign (either positive or negative) are added, the sum
has the same sign as the two integers.
Addition of integers having same signs
From zero, move to the first number 4. Since the second number is positive, we
move 3 places to the right from 4 to reach 7.
Ex 1. Add 4 and 3 on the number line.

7. 7
Ex 2. Add–5 and –4 on the number line
From zero, move to the first number –5, since the second number is
negative, we move 4 places to the left from–5 to reach –9.
Solution:
(-5) + (-4)= -9

8. 8
Ex 3. Add 4 and (–2) on the number line.
Start from zero and move to the first number 4. Since the second
number is negative, we move 2 steps left from 4 to reach 2.
Solution:
(4) + (-2)= 2
Addition of one positive and one negative
integer

9. 9
Ex4. Add (–4) and 5 on the number line.
Solution:
From zero, move to the first number –4. Since the second number is
positive, we move 5 places to the right from–4 to reach 1.
(-4) + 5 = 1

10. 10
Subtraction of Integers using a Number Line
Rule: 1.For any two integers a and b,
a–b = a + (additive inverse of b) = a + (–b)
2.For any two integers a and b,
a – (–b) = a + (additive inverse of (–b)) = a + b
Ex 1. Subtract 3 from 5 using a number line
Solution: 5 – 3 = 5 + (additive inverse of 3) = 5 +(-3)
Now this is the same as addition of two integers as studied earlier.
From zero, move to the first number 5. Since the second number is
negative, we move 3 places to the left from 5 to reach 2.
∴ 5 + (–3) = 5 – 3 = 2

11. 11
Ex 2. Subtract (–5) from 4 using a number line.
Solution:
4 - (-5) = 4 + (additive inverse of -5) = 4 + 5
From zero, move to the first number 4. Since the second number is
positive, we move 5 places to the right from 4 to reach 9.
∴ 4–(–5)=4+5=9

12. 12
Ex 3. Subtract 3 from (–6) using a number line.
Solution:
(-6) - 3 = (-6) + (additive inverse of 3) = (-6) + (-3)
From zero, move to the first number –6. Since the second number is
negative, we move 3 places to the left from–6 to reach –9.
∴ (–6) – 3 = (–6) + (–3) = (–9)

13. 13
Ex 4. Subtract –2 from –5 using a number line
Solution:
(-5) – (-2) = (-5) + (additive inverse of -2) = (-5) + 2
From zero, move to the first number –5. Since the second number is
positive, we move 2 places to the right from –5 to reach –3.
∴ (–5) – (–2) = (–5) + 2 = (–3)

14. 14
HOME WORK
1. Represent the following as integers with the proper sign.
a. A loan of Rs 5000 taken from a bank.
b. A gain of 8 kilogram.
c. The bank gave an interest of Rs 500 on a deposit.
d. The temperature of Shimla is 7 degrees Celsius below zero.
e. 285 feet below sea level.
2. Insert the correct sign‘<’,‘>’,or‘=’ in the boxes given below.
a. 2 □ 5 b. 4 □ –5 c. 3 □ -3 d. –9 □ –6
e. 31 □ –87 f. 10 □ -14
3. Arrange the following integers in the ascending order.
a. 26, –45, 92, –74 b. 12, –8, –3, 0
4. Arrange the following integers in the descending order.
a. 45, 37, –88, 25 b. 152, 169, –104, –117
5. Write the predecessor and the successor of the following integers.
a. 78 b. (–37) c. (–7) d. 0
6. Using a number line evaluate the following.
a. 5+(–8) b. (–10)+(–6) c. 1+(–9) d. (–3)–(–11)
e. 4–(–7) f. (–2)+12 g. 8+(–3)+5 h. (–6)+9

15. 15
7. A number line representing integers is given below.
Write the integers represented by A, B, C, D, E.