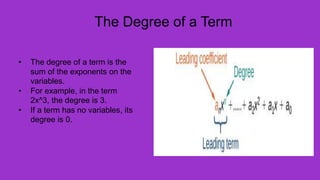
A polynomial is an algebraic expression made up of one or more terms combined using addition and subtraction. A term consists of a number called the coefficient multiplied by one or more variables raised to a non-negative integer power. The degree of a term is the sum of the exponents on the variables, and the degree of a polynomial is the highest degree among its terms. Polynomials can be classified based on the number of terms as monomials, binomials, trinomials, or polynomials with a degree greater than three.

1. Introduction to Polynomials
What are Polynomials?

2. Understanding Terms in Algebra
• Terms are the building blocks
of algebraic expressions.
• A term can be a constant, a
variable, or a combination of
both.
• For example, 2x, 3, and x^2
are all terms.

3. Coefficients and Variables in Terms
• A coefficient is the number
that multiplies the variable in
a term.
• For example, in the term 3x, 3
is the coefficient.
• The variable in a term
represents an unknown value.

4. Creating Polynomials from Terms
• A polynomial is an expression
that consists of one or more
terms.
• Polynomials can be created
by combining terms using
addition or subtraction.
• For example, 3x + 2x^2 5 is a
polynomial with three terms.

5. Types of Polynomials: Monomials, Binomials,
Trinomials, and Beyond
• A monomial is a polynomial
with only one term.
• A binomial is a polynomial
with two terms.
• A trinomial is a polynomial
with three terms.
• Polynomials with more than
three terms are called
polynomials with degree
greater than three.

6. Identifying Terms in a Polynomial
• To identify the terms in a
polynomial, look for the
addition or subtraction signs.
• Each term should be
separated by these signs.
• For example, in the
polynomial 3x + 2x^2 5, there
are three terms.

7. The Degree of a Term
• The degree of a term is the
sum of the exponents on the
variables.
• For example, in the term
2x^3, the degree is 3.
• If a term has no variables, its
degree is 0.

8. The Degree of a Polynomial
• The degree of a polynomial is
the highest degree of its
terms.
• For example, in the
polynomial 3x^2 + 2x 5, the
degree is 2.
• If a polynomial has only one
term, its degree is equal to
the degree of that term.

9. Arranging Polynomials in Order
• Polynomials are often
arranged in standard form,
which is from highest to
lowest degree.
• For example, the polynomial
3x^2 2x + 1 is in standard
form.
• When rearranging a
polynomial, make sure to
keep the terms in the same
order, but rearrange the
coefficients.

10. Positive and Negative Coefficients in
Polynomials
• Polynomials can have positive
or negative coefficients.
• A positive coefficient means
the term is added, while a
negative coefficient means
the term is subtracted.
• For example, in the
polynomial 2x^2 3x + 5, the
first term has a positive
coefficient, the second term
has a negative coefficient,
and the third term has a
positive coefficient.