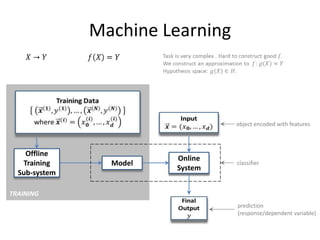
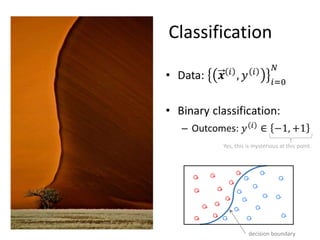
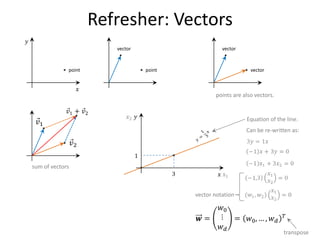
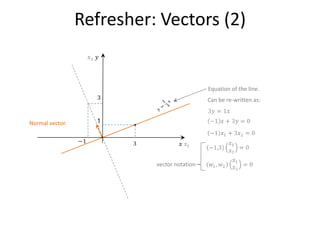
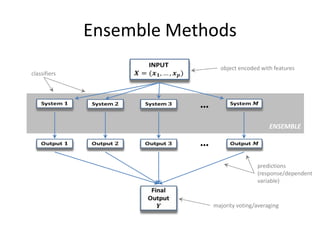
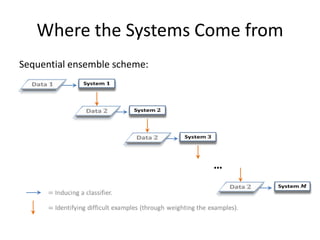
This document provides an overview of machine learning techniques including categorization, popularity, and sequence labeling applications. It outlines the goals of introducing important machine learning concepts and illustrating techniques through examples. The tutorial aims to be self-contained and explain notation. The outline includes examples of machine learning applications, encoding objects with features, the machine learning framework, linear models, tree models, boosting, ranking evaluation, and sequence labeling with hidden Markov models.

1. Machine Learning
with Applications in Categorization, Popularity and Sequence labeling
(linear models, decision trees, ensemble methods, evaluation)
Dr. Nicolas Nicolov
<1st_last@yahoo.com>

2. Goals
• Introduce important ML concepts
• Illustrate ML techniques through examples in:
– Categorization
– Popularity
– Sequence labeling
(tutorial aims to be self-contained and to explain the notation)
2

3. Outline
• Examples of applications of Machine Learning
• Encoding objects with features
• The Machine Learning framework
• Linear models
– Perceptron, Winnow, Logistic Regression, Robust Risk Minimization (RRM)
• Tree models (Decision Trees DTs)
– Classification Decision Trees, Regression Trees
• Boosting
– AdaBoost
• Ranking evaluation
– Kendall tau and Spearman’s coefficient
• Sequence labeling
– Hidden Markov Models (HMMs)
3

4. EXAMPLES OF MACHINE LEARNING
Why?– Get a flavor of the diversity of areas where ML is applied.
4

5. Sequence Labeling
(like search query analysis)
Geo-Political Entity
PER_ _PER_ _PER X GPE
George W. Bush discussed Iraq
<PER>George W. Bush</PER> discussed <GPE>Iraq</GPE>
George W. Bush discussed Iraq
5

6. Spam
www.dietsthatwork.com
www . dietsthatwork . com
further segmentation
www . diets that work . com
classification
SPAM!
6

7. Tokenization
What!?I love the iphone:-)
What !? I love the iphone :-)
How difficult can that be? — 98.2% [Zhang et al. 2003]
NO TRESSPASSING
VIOLATORS WILL
BE PROSECUTED
7

8. NL Parsing
syntactic structure
PREP CONTR
DOBJ
MANR
POSS
SUBJ DET
DET MOD
MOD MOD
Unlike my sluggish Chevy the Audi handles the winding mountain roads superbly
8

9. State Transitions
LEFTARC:
λ λ β
RIGHTARC:
λ λ β
λ β
NOARC:
λ λ β
SHIFT:
using ML to make the decision
λ λ β
which action to take 9

10. Two Ladies in a Men’s Club
10

11. SUBJ IOBJ
We serve men
We serve food to men.
We serve our community.
serve —IndirectObject men
SUBJ DOBJ
We serve men
We serve organic food.
We serve coffee to connoiseurs.
serve —DirectObject men
11

12. Coreference
Audi is an automaker that makes luxury cars
and SUVs. The company was born in
Germany .
It was established by August Horch in
1910. Horch had previosly founded another
company and his models were quite
popular. Audi started with four cylinder
models. By 1914, Horch 's new cars were
racing and winning.
August Horch left the Audi company in
1920 to take a position as an industry
representative for the German motor
vehicle industry federation.
Currently Audi is a subsidiary of the
Volkswagen group and produces cars of
outstanding quality.
12

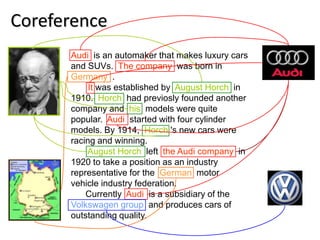
13. Parts of Objects (Meronymy)
[…] the interior seems upscale with leatherette upholstery that looks and
feels better than the real cow hide found in more expensive vehicles, a
dashboard accented by textured soft-touch materials, a woven mesh
headliner, and other materials that give the New Beetle’s interior a
sense of quality. […] Finally, and a big plus in my book, both front seats were
height adjustable, and the steering column tilted and telescoped for
optimum comfort.
13

14. Sentiment Analysis
Positive Negative
Xbox
Xbox
I love pineapple nearly as much as I hate bananas.
POSITIVE sentiment regarding topic pineapple.
14

15. Chinese Sentiment
Sentence
Car aspects Sentiment categories
15

16. 16

17. 17

18. Categorization
• High-level task:
– Given a restaurant what is its restaurant sub-category?
• Encoding entities with features
• Feature selection non-standard order
• Linear models “Though this be madness,
yet there is method in't.”
18

19. Roadmap
• Examples of applications of Machine Learning
• Encoding objects with features
• The Machine Learning framework
• Linear models
– Perceptron, Winnow , Logistic Regression, Robust Risk Minimization (RRM)
• Tree models (Decision Trees DTs)
– Classification Decision Trees, Regression Trees
• Boosting
– AdaBoost
• Ranking evaluation
– Kendall tau and Spearman’s coefficient
• Sequence labeling
– Hidden Markov Models (HMMs)
19

20. ENCODING OBJECTS WITH FEATURES
Why?– ML algorithms are “generic”; most of them are cast as solutions around vector encodings of the
domain objects. Regardless of the ML algorithm we will need to represent/encode the domain objects as
feature vectors. How well we do this (the quality of features) directly impacts system performance.
20

21. Flat
Object
Encoding
Can be a set;
object can belong Number of
to several classes. features can
be millions.
37 1 0 0 1 1 1 0 1 …
Machine learning (training) instance/example/observation. 21

22. Structured Objects
to Strings
to Features Table can be quite large.
Structured object: Feature string Feature index
Read as field “f2:f4” contains feature “a”. *DEFAULT* 0
f1 … …
f2 f2:f4>a 100
f4 abcde
“f2:f4>a” f2:f4>b 101
f5 “f2:f4>b” uni-grams
“f2:f4>c” f2:f4>c 102
f3 … … …
f6 “f2:f4>a_b” f2:f4>a_b 105
“f2:f4>b_c” bi-grams
“f2:f4>c_d” f2:f4>b_c 106
… f2:f4>c_d 107
“f2:f4>a_b_c”
tri-grams … …
“f2:f4>b_c_d”
f2:f4>a_b_c 109 22

23. Sliding Window (bi-grams)
SkyCity at the Space Needle
add initial “^” and final “$” tokens
^ SkyCity at the Space Needle $
sliding window
^ SkyCity at the Space Needle $
^ SkyCity at the Space Needle $
^ SkyCity at the Space Needle $
^ SkyCity at the Space Needle $
23

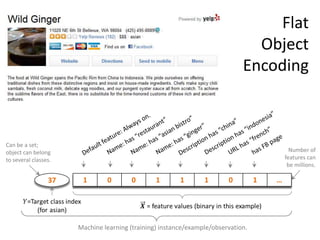
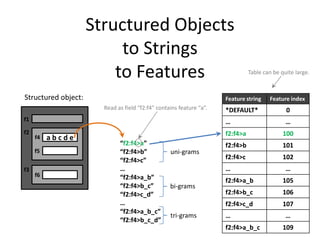
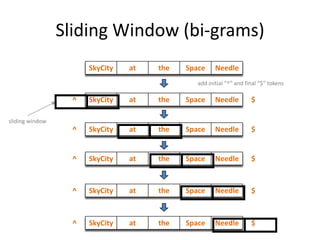
24. Example: Feature Templates
public static List<string> NGrams( string field ) could add field name as argument and prefix all features
{
var featutes = new List<string>();
string[] tokens = field.Split( spaceCharArr, System.StringSplitOptions.RemoveEmptyEntries );
featutes.Add( string.Join( "", field.Split(SPLIT_CHARS) ) ); // the entire field
string unigram = string.Empty, bigram, previous1 = "^", previous2 = "^", trigram;
for (int i = 0; i < tokens.Length; i++)
{
unigram = tokens[ i ];
featutes.Add(unigram);
bigram = previous1 + "_" + unigram; initial bigram is “^_tokens*0]"
featutes.Add( bigram );
if ( i >= 1 ) { trigram = previous2 + "_" + bigram; featutes.Add( trigram ); }
previous2 = previous1;
initial tri-gram is: "^_tokens[0]_tokens[1] "
previous1 = unigram;
}
featutes.Add( unigram + "_$" );
featutes.Add( bigram + "_$" ); last trigram is “tokens*tokens.Length-2]_tokens[tokens.Length-1]_$"
return result;
24
}

25. The Art of Feature Engineering:
Disjunctive Features
• Useful feature = triggers often and with a particular class.
• Rarely occurring (but indicative of a class) features can be
combined in a disjunction. This results in:
– Need for less data to achieve good performance.
– Final system performance (with all available data) is higher.
• How can we get insights about such features: Error analysis!
Regex ITALIAN_FOOD = new Regex(@"al dente|agnello|alfredo|antipasti|antipasto|arrabbiata|bistecca|bolognese|
branzino|caprese|carbonara|carpaccio|cioppino|cozze|fettuccine|filetto|focaccia|frutti di mare|funghi|
gnocchi|gorgonzola|insalata|lasagna|linguine|linguini|macaroni|minestrone|mozzarella|ossobuco|panini| panino|
parmigiana|pasticcio|pecorino|penne|pepperoncini|pesce|pesto|piatti|piatto|piccata|polpo|pomodori|prosciutto|
radicchio|ravioli|ricotta|rigatoni|risotto|saltimbocca|scallopini|scaloppini|spaghetti|tagliatelle|tiramisu|
tortellini|vitello|vongole");
if (ITALIAN_FOOD.Match(entity.description).Success) features.Add("Italian_Food_Matched_Description");
Triggering of the feature. Up to us how we call the feature.
25

26. Generic Nature of ML Systems
human sees
Indices of (binary) features that trigger.
instance( class= 7, features=[0,300857,100739,200441,...])
computer “sees” instance( class=99, features=[0,201937,196121,345758,13,...])
instance( class=42, features=[0,99173,358387,1001,1,...])
...
Number of features that trigger for individual
instances are often not the same. 26
Default feature always triggers.

27. Training Data
Instance /w outcome.
27

28. Feature Selection
• Templates: powerful way to get lots of features.
• We get too many features. e.g., 20M for dependency parsing.
• Danger of overfitting. Doing well on seen data but poorly on unseen data.
• Feature selection: Automatic ways of finding discriminative features.
– CountCutOff.
– TFxIDF.
– Mutual information.
– Information gain.
– Chi square. We will examine in detail the implementation of this.
28

29. Mutual Information
29

30. Information Gain
Balances effects of feature triggering for an object with
the effects of feature being absent for an object.
30

31. Chi Square
float Chi2(int a, int b, int c, int d) {
return (a+b+c+d)* ((a*d-b*c)^2) / ((a+b)*(a+c)*(c+d)*(b+d));
}
31

32. Exponent(Log) Trick
While the final output may not be big intermediate results are. Solution:
float Chi2(int a, int b, int c, int d)
{
return
(a+b+c+d) * ((a*d-b*c)^2) /
((a+b)*(a+c)*(c+d)*(b+d));
}
float Chi2_v2(int a, int b, int c, int d)
{
double total = a + b + c + d;
double n = Math.Log(total);
double num = 2.0 * Math.Log(Math.Abs((a * d) - (b * c)));
double den = Math.Log(a + b) + Math.Log(a + c) + Math.Log(c + d) + Math.Log(b + d);
return (float) Math.Exp(n+num-den);
32
}

33. Chi Square: Score per Feature
33

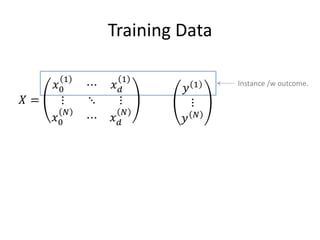
34. Chi Square Feature Selection
int[] featureCounts = new int[ numFeatures ];
int numLabels = labelIndex.Count;
int[] classTotals = new int[ numLabels ]; // instances with that label.
float[] classPriors = new float[ numLabels ]; // class priors: classTotals[label]/numInstances.
int[,] counts = new int[ numLabels, numFeatures ]; // (label,feature) co-occurrence counts.
int numInstances = instances.Count;
... Do a pass over the data and collect above counts.
float[] weightedChiSquareScore = new float[ numFeatures ];
for (int f = 0; f < numFeatures; f++) // f is a feature index
{
float score = 0.0f;
for (int labelIdx = 0; labelIdx < numLabels; labelIdx++)
{
int a = counts[ labelIdx, f ];
int b = classTotals[ labelIdx ] - p;
int c = featureCounts[ f ] - p;
int d = numInstances - ( p + q + r );
if (p >= MIN_SUPPORT && q >= MIN_SUPPORT) { // MIN_SUPPORT = 5
score += classPriors[ labelIdx ] * Chi2( a, b, c, d );
}
}
Weighted average across all classes.
weightedChiSquareScore[ f ] = score;
} 34

35. ⇒ Summary: Encoding
• Object representation is crucial.
• Humans: good at suggesting features (templates).
• Computers: good at filtering (feature selection).
The system designer does not have to worry about which feature is more
important or useful, and the job is left to the learning algorithm to assign
appropriate weights to the corresponding features. The system designer’s job
is to define a set of features that is large enough to represent most of the
useful information, yet small enough to be manageable for the algorithms and
the infrastructure.
• Feature engineering: Ensuring systems use the “right”
features.
35

36. Roadmap
• Examples of applications of Machine Learning
• Encoding objects with features
• The Machine Learning framework
• Linear models
– Perceptron, Winnow , Logistic Regression, Robust Risk Minimization (RRM)
• Tree models (Decision Trees DTs)
– Classification Decision Trees, Regression Trees
• Boosting
– AdaBoost
• Ranking evaluation
– Kendall tau and Spearman’s coefficient
• Sequence labeling
– Hidden Markov Models (HMMs)
36

37. MACHINE LEARNING
GENERAL FRAMEWORK
37

38. Machine Learning: Representation
Complex decision making:
prediction
(response/dependent variable).
input/independent variable
Can be qualitative/quantitative
(classification/regression).
classifier
38

39. Notation
39

40. Machine Learning
object encoded with features
Offline
Online
Training Model classifier
System
Sub-system
TRAINING
prediction
(response/dependent variable)
40

41. Classes of Learning Problems
• Classification: Assign a category to each item (Chinese |
French | Indian | Italian | Japanese restaurant).
• Regression: Predict a real value for each item (stock/currency
value, temperature).
• Ranking: Order items according to some criterion (web search
results relevant to a user query).
• Clustering: Partition items into homogeneous groups
(clustering twitter posts by topic).
• Dimensionality reduction: Transform an initial representation
of items into a lower-dimensional representation while
preserving some properties (preprocessing of digital images).
41

42. ML Terminology
• Examples: Items or instances used for learning or evaluation.
• Features: Set of attributes represented as a vector associated with an example.
• Labels: Values or categories assigned to examples. In classification the labels are categories; in
regression the labels are real numbers.
• Target: The correct label for a training example. This is extra data that is needed for supervised
learning.
• Output: Prediction label from input set of features using a model of the machine learning algorithm.
• Training sample: Examples used to train a machine learning algorithm.
• Validation sample: Examples used to tune parameters of a learning algorithm.
• Model: Information that the machine learning algorithm stores after training. The model is used
when predicting the output labels of new, unseen examples.
• Test sample: Examples used to evaluate the performance of a learning algorithm. The test sample is
separate from the training and validation data and is not made available in the learning stage.
• Loss function: A function that measures the difference/loss between a predicted label and a true
label. We will design the learning algorithms so that they minimize the error (cumulative loss across
all training examples).
• Hypothesis set: A set of functions mapping features (feature vectors) to the set of labels. The
learning algorithm chooses one function among those in the hypothesis set to return after training.
Usually we pick a class of functions (e.g., linear functions) parameterized by a set of free parameters
(e.g., coefficients of the linear function) and pinpoint the final hypothesis by identifying the
parameters that minimize the error.
• Model selection: Process for selecting the free parameters of the algorithm (actually of the function
in the hypothesis set). 42

43. Classification
Yes, this is mysterious at this point.
+ −
+ + − −
+
−
+ + −
− −
+ −
+
+ −
−
+ −
+ − −
43
decision boundary

44. Multi-Class Classification
44

45. One-Versus-All (OVA)
For each category in turn, create a binary classifier
where an instance in the data belonging to the
category is considered a positive example, all other
examples are considered negative examples.
Given a new object, run all these binary classifiers
and see which classifier has the “highest
prediction”.
The scores from the different classifiers need to be
calibrated!
45

46. One-Versus-One (OVO)
For each pair of classes, create binary classifier
on data labeled as either of the classes.
How many such classifiers?
Given a new instance run all classifiers and
predict class with maximum number of wins.
46

47. Errors
“Nobody is perfect, but then again, who wants to be nobody.”
Average error across all instances.
Goal: Minimize the Error.
Beneficial to have differentiable loss function.
#misclassified examples
(penalty score of 1 for every misclassified example).
47

48. Error: Function of the Parameters
The cumulative error across all instances is a function of the parameters.
1
2
48

49. Evaluation
• Motivation:
– Benchmark algorithms (which system is better).
– Tuning parameters during training.
49

50. Evaluation Measures
GeneralizationError: Probability to misclassify an instance selected according
to the distribution of the labeled instance space
TrainingError: Percentage of training examples which are correctly classified.
Optimistically biased estimate especially
if the inducer over-fits the (training) data.
Empirical estimation of the generalization error:
• Heldout method
• Re-sampling:
1. Random resampling
2. Cross-validation
50

51. Precision, Recall and F-measure
General Setup
Let’s consider binary classification:
Space of all instances
System identified these as
negative and got them correct
(true negative).
System identified
these as positive System identified System identified
but got them these as positive these as negative
wrong but got them but got them
(false positive). correct wrong
(true positive). (false negative).
Instances identified as Positive instances in reality.
positive by the system.
51

52. Definitions
Accuracy, Precision, Recall,
and F-measure
TN: true negatives Precision:
FP: false positives
TP:
true positives
FN: false negatives
Recall:
F-measure: Harmonic mean of
Accuracy: precision and recall
52

53. Accuracy vs. Prec/Rec/F-meas
Accuracy can be misleading for evaluating a model with an imbalanced distribution of
the class. When there are more majority class instances than minority class instances,
predicting always the majority class gives good accuracy.
Precision and recall (together) are better indicators.
As a single, aggregate number f-measure favors the lower of the precision or recall.
53

54. Extreme Cases for Precision & Recall
all instances
TN: true negatives
TP:
true positive
FN: false negatives
system actual
all instances system
FP: false positives
TP: true positives
Precision can be traded for recall and vice 54
versa.
actual

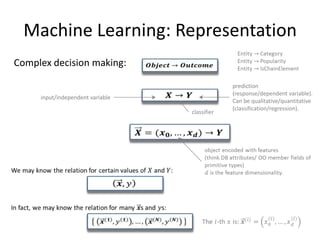
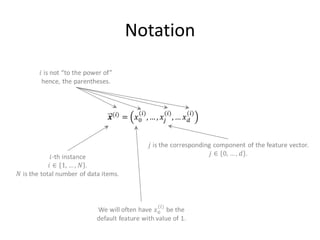
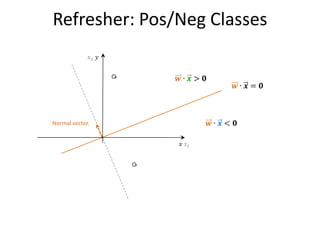
55. Definitions
Sensitivity & Specificity
TN: true negatives
FP: false positives
[same as recall;
TP: aka true positive rate]
true positives
FN: false negatives
[aka true negative rate]
False positive rate: False negative rate:
55

56. Venn Diagrams
These visualization diagrams were introduced by John Venn:
John Venn (1880) “On the Diagrammatic and Mechanical
Representation of Propositions and Reasonings”, Philosophical
Magazine and Journal of Science, 5:10(59).
What if there are three classes?
Four classes?
With more classes our visual intuitions
are helping less and less.
A subtle point: These are just the
actual/real classes without the system
Six classes? classes drawn on top!
56

57. Confusion Matrix
Shows how the predictions of instances of an actual class are distributed across all classes.
Here is an example confusion matrix for three classes:
Predicted class A Predicted class B Predicted class C
Number of instances Number of instances
in the actual class A in the actual class A Total number of actual
Actual class A …
AND predicted as BUT predicted as instances of class A
belonging to class A. belonging to class B.
Total number of actual
Actual class B … … …
instances of class B
Total number of actual
Actual class C … … …
instances of class C
Total number of Total number of Total number of Total number of instances
instances predicted instances predicted instances predicted
as class A as class B as class C
Counts on the diagonal are the true positives for each class. Counts not on the diagonal are errors.
Confusion matrices can handle many classes. 57

58. Confusion Matrix:
Accuracy, Precision and Recall
Given a confusion matrix, it’s easy to compute accuracy, precision and recall:
Predicted class A Predicted class B Predicted class C
Actual class A 50 80 70 200
Actual class B 40 140 120 300
Actual class C 120 220 160 500
210 440 350 1000
58
Confusion matrices can, themselves, be confusing sometimes 

59. Roadmap
• Examples of applications of Machine Learning
• Encoding objects with features
• The Machine Learning framework
• Linear models
– Perceptron, Winnow , Logistic Regression, Robust Risk Minimization (RRM)
• Tree models (Decision Trees DTs)
– Classification Decision Trees, Regression Trees
• Boosting
– AdaBoost
• Ranking evaluation
– Kendall tau and Spearman’s coefficient
• Sequence labeling
– Hidden Markov Models (HMMs)
59

60. LINEAR MODELS
Why?– Linear models are good way to learn about core ML concepts.
60

61. Refresher: Vectors
vector vector
point point vector
points are also vectors.
Equation of the line.
Can be re-written as:
sum of vectors
vector notation
61
transpose

62. Refresher: Vectors (2)
Equation of the line.
Can be re-written as:
Normal vector.
vector notation
62

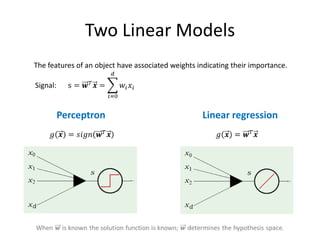
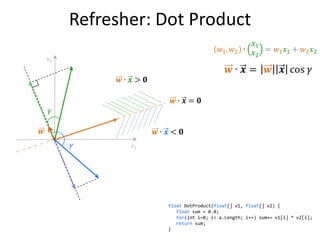
63. Refresher: Dot Product
float DotProduct(float[] v1, float[] v2) {
float sum = 0.0;
for(int i=0; i< a.Length; i++) sum+= v1[i] * v2[i];
return sum;
} 63

64. Refresher: Pos/Neg Classes
+
Normal vector.
−
64

65. sgn Function
In mathematics:
We will use:
Informally drawn as:
65

66. Two Linear Models
The features of an object have associated weights indicating their importance.
Signal:
Perceptron Linear regression
66

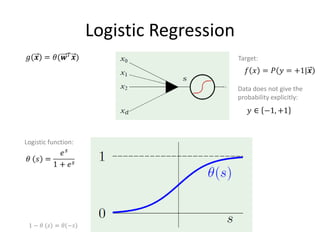
67. Why “Regression”?
Why the term for quantitative output prediction is “regression”?
“That same year [1875], [Francis] Galton decided to recruit some of his friends for an experiment with
sweet peas. He distributed seeds among seven of them, asking them to plant the seeds and return the
offspring. Galton measured the baby seeds and compared their diameters to those of their parents. He
noticed a phenomenon that initially seems counter-intuitive: the large seeds tended to produce smaller
offspring, and the small seeds tended to produce larger offspring. A decade later he analyzed data from his
anthropometric laboratory and recognized the same pattern with human heights. After measuring 205
pairs of parents and their 928 adult children, he saw that exceptionally tall parents had kids who were
generally shorter than they were, while exceptionally short parents had children who were generally taller
than their parents.
After reflecting upon this, we can understand why it must be the case. If very tall parents always produced
even taller children, and if very short parents always produced even shorter ones, we would by now have
turned into a race of giants and midgets. Yet this hasn't happened. Human populations may be getting
taller as a whole – due to better nutrition and public health – but the distribution of heights within the
population is still contained.
Galton called this phenomenon ‘regression towards mediocrity in hereditary stature’. The concept is now
more generally known as regression to the mean.”
[A.Bellos pp.375]
67

68. On-Line (Sequential) Learning
• On-line = process one example at a time.
• Attractive for large scale problems.
iteration (epoch/time).
Compute loss.
Objective: Minimize cumulative loss:
return parameters
68

69. On-Line (Sequential) Learning (2)
Sometimes written out more explicitly:
# passes over the data.
for each data item.
return parameters return parameters
69

70. Perceptron
Linearly separable data: Non-linearly separable data:
+ − + + −
+ + − + +
− − −
+ + +
− −
+ + + +
− + −
+ − − + −
− + −
+ −
+ − + − −
− −
+ − + − − −
+ − − + − −
70

71. First: Perceptron Update Rule
Simplification:
Lines pass through origin.
+
+
− + −
71

72. On-Line (Sequential) Learning
72

73. Perceptron Learning Algorithm
iteration (epoch/time).
return parameters
73

74. Perceptron Learning Algorithm
(algorithm makes multiple passes over data.)
return parameters
74

75. Perceptron Learning Algorithm (PLA)
while( mis-classified examples exist ):
Misclassified example means:
With the current weights
Update weights:
1. A challenge: Algorithm will not terminate for non-linearly separable data (outliers, noise).
2. Unstable: jump from good perceptron to really bad one within one update.
3. Attempting to minimize:
NP-hard.
75

76. Perceptron
Weight update:
76

77. Looks Simple – Does It Work?
Margin-based upper bound on updates:
Number of updates by the Perceptron Algorithm
Fact:
where: Remarkable:
Does not depend on
dimension of feature
space!
77

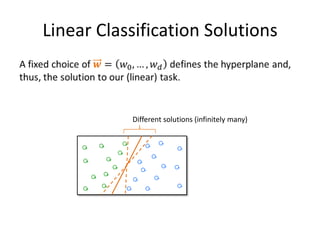
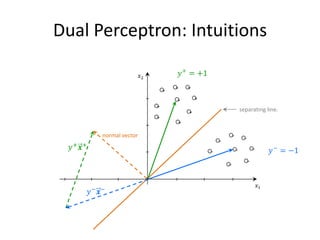
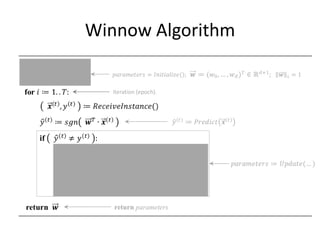
78. Compact Model Representation
Use float instead of double:
Store only non-zero weights (and indices):
Store non-zero weights and diff of indices:
void Save( StreamWriter w, int labelIdx, float[] weights )
{
w.Write( labelIdx );
int previousIndex = 0;
for (int i = 0; i < weights.Length; i++) Difference of indices.
{
if (weights[ i ] != 0.0f) {
w.Write( " " + (i - previousIndex) + " " + weights[ i ] );
previousIndex = i;
}
}
Remember last index where the weight was non-zero .
}
78

79. Linear Classification Solutions
Different solutions (infinitely many)
+ −
+ + − −
+
−
+ + −
+ − −
−
+
+ −
−
+ −
+ − −
79

80. The Pocket Algorithm
A better perceptron algorithm:
Keep track of the error and update weights when we lower the error.
Compute error. Expensive step!
Access to the entire data needed!
Only update the best weights
if we lower the error!
80

81. Voted Perceptron
• Training as the usual perceptron algorithm (with some extra book-keeping).
• Decision rule:
iterations
81

82. Dual Perceptron: Intuitions
+ +
+
+ +
+
+ separating line.
+
+
normal vector − −
−
− −
−
−
−
82

83. Dual Perceptron
(algorithm makes multiple passes over data.)
return parameters
Decision rule:
83

84. Exclusive OR (XOR) Function
Truth table: Inputs in and color-coding
of the output:
Challenge:
The data is not linearly separable ???
(no straight line can be drawn
that separates the green from the
blue points).
84

85. Solution for the Exclusive OR (XOR)
We introduce
another input
dimension:
Now the data is linearly separable:
85

86. Winnow Algorithm
iteration (epoch).
Normalizing constant.
Multiplicative
update.
return parameters
86

87. Training, Test Error and Complexity
Test error
Training error
Model complexity
87

88. Logistic Regression
Target:
Data does not give the
probability explicitly:
Logistic function:
88

89. Logistic Regression
Data likelihood:
Negative log-likelihood:
Error:
89

90. Derivative:
Refresher
Chain rule:
Partial derivative:
Gradient (derivatives with respect to each component):
This is a vector and we
Gradient of the error: can compute it at a point. 90

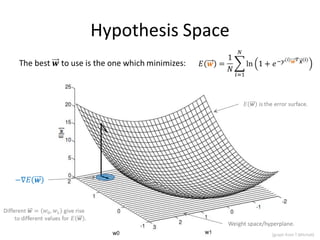
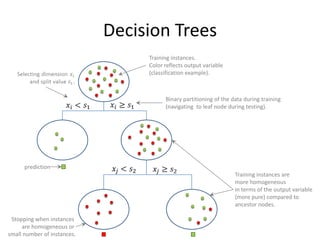
91. Hypothesis Space
Weight space/hyperplane.
91
[graph from T.Mitchell]

92. Math Fact
The gradient of the error:
(a vector in weight space) specifies the direction of the argument that leads to the
steepest increase for the value of the error.
The negative of the gradient gives the direction of the steepest decrease.
Negative gradient (see next slides).
92

93. Computing the Gradient
Because gradient is a linear operator.
93

94. (Batch) Gradient Descent
repeat
Compute gradient:
Update weights:
max #iterations;
marginal error improvement; and
small value for the error.
94

95. Punch Line
The new object is in the class if:
classification rule.
95

96. Newton’s Method
2.5
2
1.5
1
0.5
0
0 0.5 1 1.5 2 2.5 3
-0.5
96

97. Newton-Raphson
97

98. Robust Risk Minimization
Notation:
input vector
label
training examples
weight vector
bias
continuous linear model
Prediction rule:
Classification error:
98

99. Robust Classification Loss
Parameter estimation:
Hinge loss:
Robust classification loss:
99

100. Loss Functions: Comparison
100

101. Confidence and Regularization
Confidence
Regularization:
Unconstrained optimization (Lagrange multiplier):
smaller λ corresponds to a larger A. 101

102. Robust Risk Minimization
Go over the training data.
102

103. Learning Curve
100
• Plots evaluation metric
90 Experiment with 50% of against fraction of
the training data yields training data (on the
80 evaluation number of 70.
same test set!).
70 • Highest performance
bounded by human inter
60
annotator agreement
50
(ITA).
• Leveling off effect that
40
can guide us how much
30
data is needed.
20
10
0
0% 10% 20% 30% 40% 50% 60% 70% 80% 90% 100%
Percentage of data used
for each experiment.
103

104. Summary
• Examples of ML
• Categorization
• Object encoding
• Linear models:
– Perceptron
– Winnow
– Logistic Regression
– RRM
• Engineering aspects of ML systems
104

105. PART II: POPULARITY
105

106. Goal
• Quantify how popular an entity is.
Motivation:
• Used in the new local search relevance metric.
106

107. What is popularity?
107

108. POPULARITY IN LOCAL SEARCH
108

109. Popularity
• Output a popularity score (regression)
• Ensemble methods
• Tree base procedure (non-linear)
• Boosting
109

110. When is a Local Entity Popular?
• Definition:
Visited by many people in the context of alternative choices.
• Is the popularity of restaurants the same as the popularity of
movies, etc.?
• How to operationalize “visit”, “many”, “alternative choices”?
– Initially we are using: popular means clicked more.
• Going forward we will use:
– “visit” = click given an impression.
– “choice” = density of entities in the same primary category.
– “many” = fraction of clicks from impressions. 110

111. Local Entity Popularity
The model then will be regression:
111

112. Not all Clicks are Born the Same
• Click in the context of a named query:
– Can even be argued we are not satisfying the user
information needs (and they have to click further to find out
what they are looking for).
• Click in the context of a category query:
– Much more significant (especially when alternative results
are present).
112

113. Local Entity Popularity
• Popularity & 1st page , current ranker.
• Entities without URL.
• Newly created entities.
• Clicks vs. mouseovers.
• Scenario: 50 French restaurants; best entity
has 2k clicks. 2 Italian restaurants; best entity
has 2k clicks. The French entity is more
popular because of higher available choice.
113

114. Entity Representation
9000 8000 … 4000 65 4.7 73 … 1 …
Target feature values
Machine learning (training) instance
114

115. POISSON REGRESSION
Why?– We will practice the ML machinery on a different problem, re-iterating the concepts.
Poisson regression is an example of log-linear models good for modeling counts (e.g., number
of visitors to a store in a certain time).
115

116. Setup
explanatory variables
response/outcome
variable
These counts for our scenario are the clicks on the web page.
A good way to model counts of observations is using the Poisson distribution.
116

117. Poisson Distribution: Preliminaries
The Poisson distribution realistically describes the pattern of requests over time in many client-server
situations.
Examples are: incoming customers at a bank, calls into a company’s telephone exchange, requests for
storage/retrieval services from a database server, and interrupts to a central processor. It also has higher-
dimensional applications, such as the spatial distribution of defects on integrated circuit wafers and the
volume distribution of contaminants in well water. In such cases, the “events”, which are request arrivals
or defects occurrences, are independent. Customers do not conspire to achieve some special pattern in
their access to a bank teller; rather they operate as independent agents. The manufacture of hard disks
or integrated circuits introduces unavoidable defects because the process pushes the limits of geometric
tolerances. Therefore, a perfectly functional process will still occasionally produce a defect, such as a
small area on the disk surface where the magnetic material is not spread uniformly or a shorted
transistor on an integrated circuit chip. These errors are independent in the sense that a defect at one
point does not influence, for better or worse, the chance of a defect at another point. Moreover, if the
time interval or spatial area is small, the probability of an event is correspondingly small. This is a
characterizing feature of a Poisson distribution: event probability decreases with the window of
opportunity and is linear in the limit. A second characterizing feature, negligible probability of two or
more events in a small interval, is also present in the mentioned examples.
117

118. Poisson Distribution: Formally
118

119. Poisson Distribution: Mental Steps
This comes from the theory of Generalized Linear Models (GLM).
log linear combination of the input features.
Hence, the name log-linear model.
119

120. Poisson Distribution
Data likelihood:
Log-likelihood:
120

121. Maximizing the Log-Likelihood
121

122. Roadmap
• Examples of applications of Machine Learning
• Encoding objects with features
• The Machine Learning framework
• Linear models
– Perceptron, Winnow , Logistic Regression, Robust Risk Minimization (RRM)
• Tree models (Decision Trees DTs)
– Classification Decision Trees, Regression Trees
• Boosting
– AdaBoost
• Ranking evaluation
– Kendall tau and Spearman’s coefficient
• Sequence labeling
– Hidden Markov Models (HMMs)
122

123. DECISION TREES
Why?– DTs are an influential development in ML. Combined in ensemble they provide very competitive
performance. We will see ensemble techniques in the next part.
123

124. Decision Trees
Training instances.
Color reflects output variable
(classification example).
Binary partitioning of the data during training
(navigating to leaf node during testing).
prediction
Training instances are
more homogeneous
in terms of the output variable
(more pure) compared to
ancestor nodes.
Stopping when instances
are homogeneous or 124
small number of instances.

125. Decision Tree: Example
(classification example with categorical features)
Attribute/feature/predicate
Parents
Visiting
Yes No Value of the attribute
Cinema Weather
Branching factor depends on
the number of possible values
Sunny Windy Rainy for the attribute (as seen in the
training set).
Play Stay in
tennis Money
Rich Poor Predicted classes.
Shopping Cinema 125

126. Entropy (needed for describing how an attribute is selected.)
1
Example 0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0
0 0.2 0.4 0.6 0.8 1
126

127. Selecting an Attribute: Information Gain
Measure of expected reduction in entropy.
instances attribute
127
See Mitchell’97, p.59 for an example.

128. Splitting ‘Hairs’
If there are no instances in the
current node, inherit statistics
(majority class) from parent
node.
If there are only a small number
of instances do not split the node
further (statistics are unreliable).
If there is more training data, the
128
tree can be “grown” bigger.
?

129. ID3 Algorithm
129

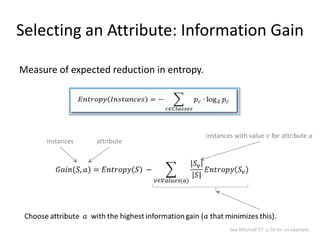
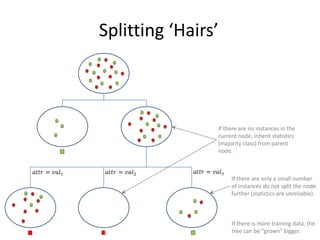
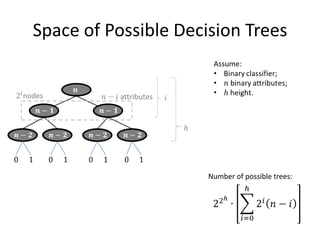
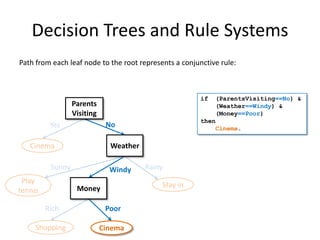
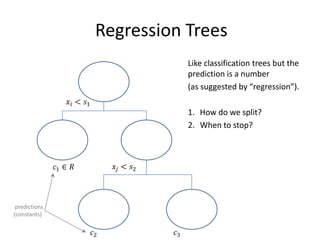
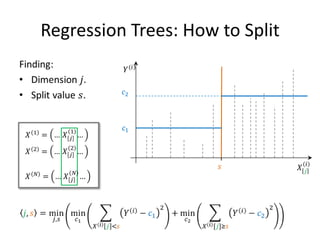
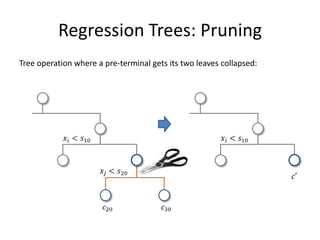
130. Alternative Attribute Selection:
Gain Ratio [Quinlan 1986]
instances attribute
Examples:
all different values.
130

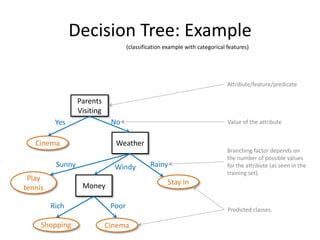
131. Alternative Attribute Selection:
GINI Index [Corrado Gini: Italian statistician]
131

132. Space of Possible Decision Trees
Number of possible trees:
132

133. Decision Trees and Rule Systems
Path from each leaf node to the root represents a conjunctive rule:
if (ParentsVisiting==No) &
Parents (Weather==Windy) &
Visiting (Money==Poor)
then
Yes No Cinema.
Cinema Weather
Sunny Windy Rainy
Play Stay in
tennis Money
Rich Poor
Shopping Cinema 133

134. Decision Trees
• Different training sample -> different resulting
tree (different structure).
• Learning does (conditional) feature selection.
134

135. Regression Trees
Like classification trees but the
prediction is a number
(as suggested by “regression”).
1. How do we split?
2. When to stop?
predictions
(constants)
135

136. Regression Trees: How to Split
136

137. Regression Trees: Pruning
Tree operation where a pre-terminal gets its two leaves collapsed:
137

138. Regression Trees: How to Stop
1. Don’t stop.
2. Build big tree.
3. Prune.
4. Evaluate sub-trees.
138

139. Roadmap
• Examples of applications of Machine Learning
• Encoding objects with features
• The Machine Learning framework
• Linear models
– Perceptron, Winnow , Logistic Regression, Robust Risk Minimization (RRM)
• Tree models (Decision Trees DTs)
– Classification Decision Trees, Regression Trees
• Boosting
– AdaBoost
• Ranking evaluation
– Kendall tau and Spearman’s coefficient
• Sequence labeling
– Hidden Markov Models (HMMs)
139

140. BOOSTING
140

141. Ensemble Methods
object encoded with features
classifiers
…
ENSEMBLE
…
predictions
(response/dependent
variable)
majority voting/averaging
141

142. Where the Systems Come from
Sequential ensemble scheme:
…
142

143. Contrast with Bagging
Non-sequential ensemble scheme:
DATA
Datai are independent of each other (likewise for Sytemi).
143

144. Data System
Base Procedure:
Decision Tree
Training instances.
Color reflects output variable
(classification example).
Binary partitioning of the data during training
(navigating to leaf node during testing).
prediction
Training instances are
more homogeneous
in terms of the output variable
(more pure) compared to
ancestor nodes.
Stopping when instances
are homogeneous or 144
small number of instances.

145. Ensemble Scheme
TRAINING DATA
base procedure
base procedure Small systems.
Original data
Don’t need to be
perfect.
base procedure
Weighted data
base procedure
Weighted data
Final prediction (regression)
145

146. Ada Boost (classification)
Original data
Weighted data
Weighted data
Weighted data
normalizing factor.
final prediction.
146

147. AdaBoost
Initializing weights.
weight update.
normalizing factor.
final prediction.
147

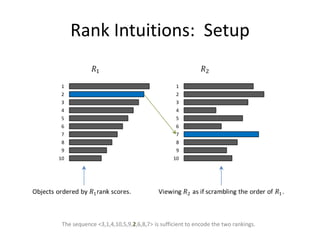
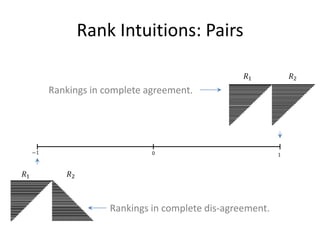
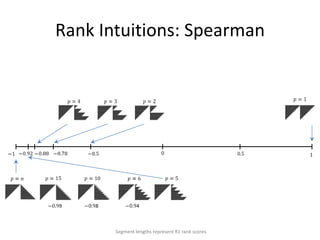
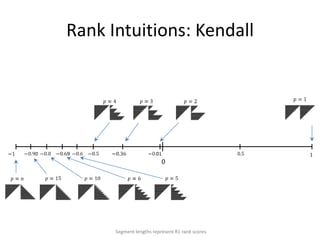
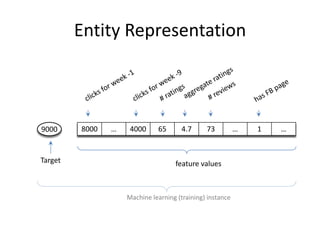
148. Binary Classifier
• Constraint:
– Must not have all zero clicks for current week, previous week and week before last
[shopping team uses stronger constraint: only instances with non-zero clicks for
current week].
• Training:
– 1.5M instances.
– 0.5M instances (validation).
• Feature extraction:
– 4.82mins (Cosmos job).
• Training time:
– 2hrs 20mins.
• Testing:
– 10k instances: 1sec.
148

149. Roadmap
• Examples of applications of Machine Learning
• Encoding objects with features
• The Machine Learning framework
• Linear models
– Perceptron, Winnow , Logistic Regression, Robust Risk Minimization (RRM)
• Tree models (Decision Trees DTs)
– Classification Decision Trees, Regression Trees
• Boosting
– AdaBoost
• Ranking evaluation
– Kendall tau and Spearman’s coefficient
• Sequence labeling
– Hidden Markov Models (HMMs)
149

150. POPULARITY
EVALUATION
How do we know
we have a good popularity?
150

151. Rank Correlation Metrics
• •
• •
• •
The two rankings are the same.
The two rankings are reverse of each other.
Actual input is a set of objects with two rank scores (ties are possible). 151

152. Kendall’s Tau Coefficient
Considers concordant/discordant pairs in two
rankings (each ranking w.r.t. the other):
152

153. What is a concordant pair?
a a
b c
c b
Need to have the same sign
153

154. Kendall Tau: Example
A C
B D
C A
D B
Pairs:
(discordant pairs in red):
154
Observation: Total number of discordant pairs = 2x the discordant pairs in one ranking w.r.t. the other.

155. Spearman’s Coefficient
Considers ranking differences for the same object:
a a
b c
c b
Example:
155

156. Rank Intuitions: Setup
1 1
2 2
3 3
4 4
5 5
6 6
7 7
8 8
9 9
10 10
The sequence <3,1,4,10,5,9,2,6,8,7> is sufficient to encode the two rankings.
156

157. Rank Intuitions: Pairs
Rankings in complete agreement.
Rankings in complete dis-agreement.
157

158. Rank Intuitions: Spearman
Segment lengths represent R1 rank scores. 158

159. Rank Intuitions: Kendall
Segment lengths represent R1 rank scores. 159

160. What about ties?
The position of an object within set of objects with the
same scores in the rankings affects the rank correlation.
160
For example, red positioning of oj leads to lower Spearman’s coefficient; green – higher.

161. Ties
• Kendall: Strict discordance:
• Spearman:
– Can use per entity upper and lower bounds.
– Do as in the Olympics:
161

162. Ties: Kendall TauB
where:
is the number of concordant pairs.
is the number of discordant pairs.
is the number of objects in the two rankings.
http://en.wikipedia.org/wiki/Kendall_tau#Tau-b 162

163. Uses of popularity
Popularity can be used to augment gain in NDCG by linearly scaling it:
1 3 7 15 31
1 2 3 4 5
poor fair good excellent perfect
163

164. Next Steps
• How to determine popularity of new entities
– Challenge: No historical data.
– Usually there is an initial period of high popularity
(e.g., a new restaurant is featured in local
paper, promotions, etc.).
• Good abandonment (no user clicks but good
entity in terms of satisfying the user
information needs, e.g., phone number).
– Use number impressions for named queries.
164

165. References
1. Yaser S. Abu-Mostafa, Malik Magdon-Ismail & Hsuan-Tien Lin (2012) Learning From Data. AMLBook. [link]
2. Ethem Alpaydin (2009) Introduction to Machine Learning. 2nd edition. Adaptive Computation and Machine Learning series. MIT Press.
[link]
3. David Barber (2012) Bayesian Reasoning and Machine Learning. Cambridge University Press. [link]
4. Ricardo Baeza-Yates & Berthier Ribeiro-Neto (2011) Modern Information Retrieval: The Concepts and Technology behind Search. 2nd
Edition. ACM Press Books. [link]
5. Alex Bellos (2010) Alex's Adventures in Numberland. Bloomsbury: New York. [link]
6. Ron Bekkerman, Mikhail Bilenko & John Langford (2011) Scaling up Machine Learning: Parallel and Distributed Approaches. Cambridge
University Press. [link]
7. Christopher M. Bishop (2007) Pattern Recognition and Machine Learning. Information Science and Statistics. Springer. [link]
8. George Casella & Roger L. Berger (2001) Statistical Inference. 2nd edition. Duxbury Press. [link]
9. Anirban DasGupta (2011) Probability for Statistics and Machine Learning: Fundamentals and Advanced Topics. Springer Texts in Statistics.
Springer. [link]
10. Luc Devroye, László Györfi & Gábor Lugosi (1996) A Probabilistic Theory of Pattern Recognition. Springer. [link]
11. Richard O. Duda, Peter E. Hart & David G. Stork (2000) Pattern Classification. 2nd Edition. Wiley-Interscience. [link]
12. Trevor Hastie, Robert Tibshirani & Jerome Friedman (2009) The Elements of Statistical Learning: Data Mining, Inference, and Prediction.
2nd Edition. Springer Series in Statistics. Springer. [link]
13. James L. Johnson (2008) Probability and Statistics for Computer Science. Wiley-Interscience. [link]
14. Daphne Koller & Nir Friedman (2009) Probabilistic Graphical Models: Principles and Techniques. Adaptive Computation and Machine
Learning series. MIT Press. [link]
15. David J. C. MacKay (2003) Information Theory, Inference and Learning Algorithms. Cambridge University Press. [link]
16. Zbigniew Michalewicz & David B. Fogel (2004) How to Solve It: Modern Heuristics. 2nd edition. Springer. [link]
17. Tom M. Mitchell (1997) Machine Learning. McGraw-Hill (Science/Engineering/Math). [link]
18. Mehryar Mohri, Afshin Rostamizadeh & Ameet Talwalkar (2012) Foundations of Machine Learning. Adaptive Computation and Machine
Learning series. MIT Press. [link]
19. Lior Rokach (2010) Pattern Classification Using Ensemble Methods. World Scientific. [link]
20. Gilbert Strang (1991) Calculus. Wellesley-Cambridge Press. [link]
21. Larry Wasserman (2010) All of Statistics: A Concise Course in Statistical Inference. Springer Texts in Statistics. Springer. [link]
22. Sholom M. Weiss, Nitin Indurkhya & Tong Zhang (2010) Fundamentals of Predictive Text Mining. Texts in Computer Science. Springer. [link]
165

166. Roadmap
• Examples of applications of Machine Learning
• Encoding objects with features
• The Machine Learning framework
• Linear models
– Perceptron, Winnow , Logistic Regression, Robust Risk Minimization (RRM)
• Tree models (Decision Trees DTs)
– Classification Decision Trees, Regression Trees
• Boosting
– AdaBoost
• Ranking evaluation
– Kendall tau and Spearman’s coefficient
• Sequence labeling
– Hidden Markov Models (HMMs)
166

167. SEQUENCE LABELING:
HIDDEN MARKOV MODELS (HMMs)
167

168. Outline
• The guessing game
• Tagging preliminaries
• Hidden Markov Models
• Trellis and the Viterbi algorithm
• Implementation (Python)
• Complexity of decoding
• Parameter estimation and smoothing
• Second order models
168

169. The Guessing Game
• A cow and duck write an email message together.
• Goal – figure out which word is written by which animal.
169 The cow/duck illustration of HMMs is due to Ralph Grishman (NYU).

170. What’s the Big Deal ?
• The vocabularies of the cow and the duck can
overlap and it is not clear a priori who wrote a
certain word!
170

171. The Game (cont)
? ? ?
moo hello quack
COW ? DUCK
moo hello quack
171

172. The Game (cont)
DUCK
COW COW DUCK
moo hello quack
172

173. What about the Rest of the Animals?
ANT ANT ANT ANT ANT
COW COW COW COW COW
DUCK DUCK DUCK DUCK DUCK
PIG PIG PIG PIG PIG
ZEBRA ZEBRA ZEBRA ZEBRA ZEBRA
word1 word2 word3 word4 word5
173

174. A Game for Adults
• Instead of guessing which animal is associated
with each word guess the corresponding POS
tag of a word.
Pierre/NNP Vinken/NNP ,/, 61/CD years/NNS old/JJ ,/,
will/MD join/VB the/DT board/NN as/IN
a/DT nonexecutive/JJ director/NN Nov./NNP 29/CD ./.
174

175. POS Tags
"CC", "CD", "DT", "EX", "FW",
"IN", "JJ", "JJR", "JJS", "LS",
"MD","NN", "NNS","NNP", "NNPS",
"PDT", "POS", "PRP", "PRP$", "RB",
"RBR", "RBS", "RP", "SYM", "TO",
"UH", "VB", "VBD", "VBG", "VBN",
"VBP", "VBZ", "WDT", "WP", "WP$",
"WRB", "#", "$", ".",",",
":", "(", ")", "`", "``",
"'", "''"
175

176. Tagging Preliminaries
• We want the best set of tags for a sequence of words
(a sentence)
• W — a sequence of words
• T — a sequence of tags
^
T arg max P(T | W )
T
176

177. Bayes’ Theorem (1763)
likelihood prior
posterior
P(W | T ) P(T )
P(T | W )
P(W )
marginal likelihood
Reverend Thomas Bayes — Presbyterian minister (1702-1761)
177

178. Applying Bayes’ Theorem
• How do we approach P(T|W) ?
• Use Bayes’ theorem
P(W | T ) P(T )
arg max P(T | W ) arg max
T T P(W )
• So what? Why is it better?
• Ignore the denominator (and the question):
P(W | T ) P(T )
arg max P(T | W ) arg max arg max P(W | T ) P(T )
T T P(W ) T
178

179. Tag Sequence Probability
How do we get the probability P(T)
of a specific tag sequence T?
• Count the number of times a sequence occurs
and divide by the number of sequences of that
length — not likely!
– Use chain rule
179

180. Chain Rule
history
P (T ) P (t1 ,..., t n )
P (t1 ) P (t 2 | t1 ) P (t3 | t1t 2 ) ... P (t n | t1 ,..., t n 1 )
P(T) is a product of the probability of the N-grams
that make it up
Make a Markov assumption: the current tag
depends on the previous one only:
n
P(t1 ,..., tn ) P(t1 ) P(ti | ti 1 )
i 2
180

181. Transition Probabilities
• Use counts from a large hand-tagged corpus.
• For bi-grams, count all the ti–1 ti pairs
c(ti 1ti )
P(ti | ti 1 )
c(ti 1 )
• Some counts are zero – we’ll use smoothing to address
this issue later.
181

182. What about P(W|T) ?
• First it's odd—it is asking the probability of seeing “The white
horse” given “Det Adj Noun”!
– Collect up all the times you see that tag sequence and see how often “The
white horse” shows up …
• Assume each word in the sequence depends only on its
corresponding tag:
n
P(W | T ) P( wi | ti )
i 1
emission probabilities
182

183. Emission Probabilities
• What proportion of times is the word wi associated with
the tag ti (as opposed to another word):
c( wi , ti )
P( wi | ti )
c(ti )
183

184. The “Standard” Model
arg max P (T | W )
T
P (W | T ) P (T )
arg max
T P (W )
arg max P (W | T ) P (T )
T
n
arg max P ( wi | ti ) P (ti | ti 1 )
T i 1
184

185. Hidden Markov Models
• Stochastic process:
A sequence 1 , 2,… of random variables
based on the same sample space .
• Probabilities for the first observation:
P( 1 x j ) for each outcome x j
• Next step given previous history:
P( t 1 xit 1 | 1 xi1 , ... , t xit )
185

186. Markov Chain
• A Markov Chain is a stochastic process with the Markov
property:
P( t 1 xit 1 | 1 xi1 , ... , t xit ) P( t 1 xit 1 | t xit )
• Outcomes are called states.
• Probabilities for next step – weighted finite state
automata.
186

187. State Transitions w/ Probabilities
0.5
COW
0.2
1.0
END
START 0.3 0.3
0.2
DUCK
0.5
187

188. Markov Model
Markov chain 0.5 moo:0.9
where each state hello:0.1
can output signals
COW
^:1.0 0.2 $:1.0
1.0
END
START 0.3 0.3
0.2
DUCK
(like “Moore machines”): hello:0.4
quack:0.6
0.5
188

189. The Issue Was
• A given output symbol can potentially
be emitted by more than one state —
omnipresent ambiguity in natural language.
189

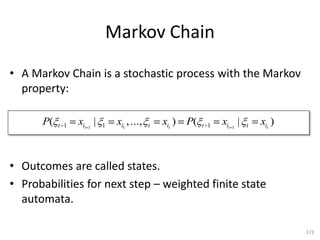
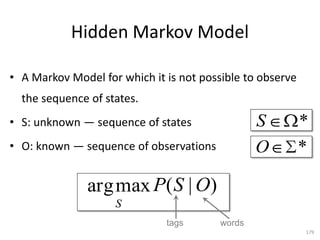
190. Markov Model
Finite set of states:
{s1,..., sm}
Signal alphabet:
{ 1,..., k }
Transition matrix:
P [ pij ] where pij P( t 1 sj | t si )
Emission probabilities:
A [aij ] where aij P( t j | t si )
Initial probability vector:
v [v1 ,..., vm ] where v j P( 1 sj)
190

191. Graphical Model
STATE TAG …
OUTPUT word
191

192. Hidden Markov Model
• A Markov Model for which it is not possible to observe
the sequence of states.
• S: unknown — sequence of states S *
• O: known — sequence of observations O *
arg max P( S | O)
S
tags words
192

193. The State Space
moo:0.9 hello:0.1
0.5 0.5
COW COW COW
1.0
0.2
0.3 0.3
START END
0.3 0.3
0.0 0.2
0.5 0.5
DUCK DUCK DUCK
hello:0.4 quack:0.6
moo hello quack
More on how the probabilities come about (training) later.
193

194. Optimal State Sequence:
The Viterbi Algorithm
We define the joint probability of the most likely sequence from
time 1 to time t ending in state si and the observed sequence O≤t
up to time t:
t (i) max P(S t 1 , t si ; O t )
S t 1
max P( 1 si1 ,..., t 1 sit 1 , t si ; O t )
si1 ,..., sit 1
194

195. Key Observation
The most likely partial derivation leading to state si at
position t consists of:
– the most likely partial derivation leading to some state sit-1
at the previous position t-1,
– followed by the transition from sit-1 to si.
195

196. Viterbi (cont)
Note:
1 (i ) vi aik 1 where vi P( 1 si ) and aik 1 P( t k1 | t si )
We will show that:
t ( j ) [max t 1 (i) pij ] a jk t
i
196

197. Recurrence Equation
t ( j) max P ( S t 1 , t s j ;O t )
S t 1
max max P ( S t 2 , t 1 si , t s j ;O t 1 , t kt )
i S t 2
max max P ( t sj; t kt |S t 2 , t 1 si ; O t 1 )
i S t 2
k1
P( S t 2 , t 1 si ; O t 1 )
max max P ( t sj | t 1 si ) P ( t kt | t sj)
i S t 2
P( S t 2 , t 1 si ; O t 1 )
[max P ( t sj | t 1 si ) max P ( S t 2 , t 1 si ; O t )]
1
i S t 2
P( t kt | t sj)
[max pij t 1 (i )] a jk t
i
197

198. Back Pointers
• The predecessor of state si in the path corresponding to
t(i) :
t ( j ) argmax ( t 1 (i ) pij )
1 i m
• Optimal state sequence:
*
s kT argmax n (i )
1 i m
* *
skt t 1
( skt 1 ) for t 1, ... , n 1
198

199. The Trellis
moo hello quack $
t=0 t=1 t=2 t=3 t=4
START 1 0 0 0 0
COW 0 0.9 0.045 0 0
0.0081
0
DUCK 0 0 0.108
0.0324
END 0 0 0 0 0.00648
199

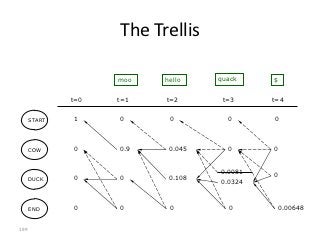
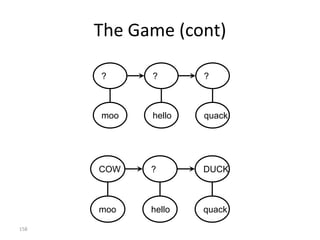
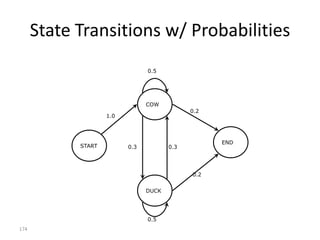
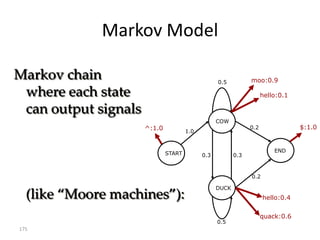
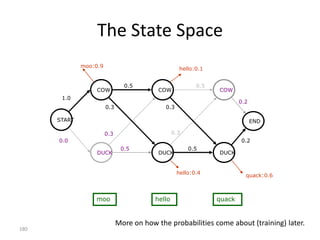
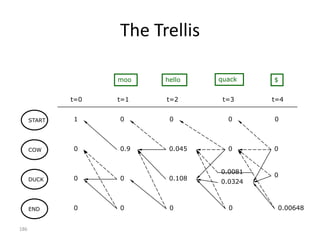
200. Implementation (Python)
observations = ['^','moo','hello','quack','$'] # signal sequence
states = ['start','cow','duck','end']
# Transition probabilities - p[FromState][ToState] = probability
p = {'start': {'cow':1.0},
'cow': {'cow' :0.5,
'duck':0.3,
'end' :0.2},
'duck': {'duck':0.5,
'cow' :0.3,
'end' :0.2}}
# Emission probabilities; special emission symbol '$' for 'end' state
a = {'cow' : {'moo' :0.9,'hello':0.1, 'quack':0.0, '$':0.0},
'duck': {'moo' :0.0,'hello':0.4, 'quack':0.6, '$':0.0},
'end' : {'moo' :0.0,'hello':0.0, 'quack':0.0, '$':1.0}}
200

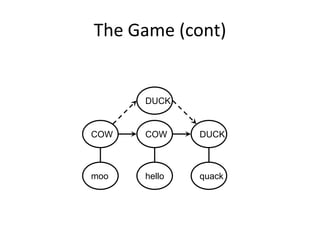
201. Implementation (Viterbi)
n = len(observations)
# Initializing viterbi table row by row; v[state][time] = prob
v = {}; for s in states: v[s] = [0.0] * T
# Initializing back pointers
backPointer = {}; for s in states: backPointer[s] = [""] * T
v['start'][0] = 1.0
for t in range(T-1): # t =[0..T-1]; populate column t+1 in v
for s in states[:-1]: # 'end' state not considered
# only consider 'start' state at time 0
if t == 0 and s != 'start': continue
for s1 in p[s].keys(): # s1 is the next state
newScore = v[s][t] * p[s][s1] * a[s1][observations[t+1]]
if v[s1][t+1] == 0.0 or newScore > v[s1][t+1]:
v[s1][t+1] = newScore
backPointer[s1][t+1] = s
201

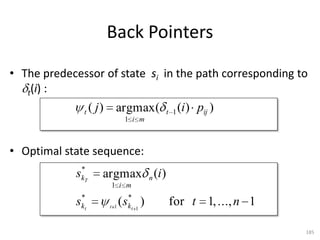
202. Implementation (Best Path)
# Now recover the optimal state sequence
state_sequence = [ 'end' ]
for t in range( n-1, 0, -1 ):
state = backPointer[ state ][ t ]
state_sequence = [ state ] + state_sequence
print "Observations....: ", observations
print "Optimal sequence: ", state_sequence
202

203. Complexity of Decoding
• O(m2n) — linear in n (the length of the string)
• Initialization: O(mn)
• Back tracing: O(n)
• Next step: O(m2)
for current_state in s1..sm # at time t+1
for prev_state in s1..sm # at time t
compute value
compare with best_so_far
• There are n next steps.
203

204. Parameter Estimation for HMMs
• Need annotated training data (Brown, PTB).
• Signal and state sequences both known.
• Calculate observed relative frequencies.
• Complications — sparse data problem (need for smoothing).
• One can use only raw data too — Baum-Welch (forward-
backward) algorithm.
204

205. Optimization
• Build vocabulary of possible tags for words
• Keep total counts for words
• If a word occurs frequently (count > threshold) consider its tag set
exhaustive
• For frequent words only consider its tag set (vs. all tags)
• For unknown words don’t consider tags corresponding to closed
class words (e.g., DT)
205

206. Applications Using HMMs
• POS tagging (as we have seen).
• Chunking.
• Named Entity Recognition (NER).
• Speech recognition.
206

207. Exercises
• Implement the training (parameter estimation).
• Use a dictionary of valid tags for known words to constrain
which tags are considered for a word.
• Implement a second-order model.
• Implement the decoder in Ruby.
207

208. Some POS Taggers
• Alias-I: http://www.alias-i.com/lingpipe
• AUTASYS: http://www.phon.ucl.ac.uk/home/alex/project/tagging/tagging.htm
• Brill Tagger: http://www.cs.jhu.edu/~brill/RBT1_14.tar.Z
• CLAWS: http://www.comp.lancs.ac.uk/computing/research/ucrel/claws/trial.html
• Connexor: http://www.connexor.com/software/tagger
• Edinburgh (LTG): http://www.ltg.ed.ac.uk/software/pos/index.html
• FLAT (Flexible Language Acquisition Tool): http://lanaconsult.com
• fnTBL: http://nlp.cs.jhu.edu/~rflorian/fntbl/index.html
• GATE: http://gate.ac.uk
• Infogistics: http://www.infogistics.com/posdemo.htm
• Qtag: http://www.english.bham.ac.uk/staff/omason/software/qtag.html
• SNoW: http://l2r.cs.uiuc.edu/~cogcomp/asoftware.php?skey=POS
• Stanford: http://nlp.stanford.edu/software/tagger.shtml
• SVMTool: http://www.lsi.upc.edu/~nlp/SVMTool
• TNT: http://www.coli.uni-saarland.de/~thorsten/tnt
• Yamcha: http://chasen.org/~taku/software/yamcha/
208

209. References
1. Brants, Thorsten. 2000. TnT – A Statistical Part-of-speech Tagger. 6th Applied NLP Conference (ANLP-2000),
224-231, Seattle, U.S.A.
2. Charniak, Eugene, Curtis Hendrickson, Neil Jacobson & Mike Perkowitz. 1993. Equations for part-of-speech
tagging. 11th National Conference on Artificial Intelligence, 784-789. Menlo Park: AAAI Press/MIT.
3. Krenn, Brigitte & Christer Samuelsson. 1997. Statistical Methods in Computational Linguistics, ESSLLI
Summer school Lecture Notes from, 11-22 August, Aix-en-Provence, France.
4. Rabiner, Lawrence R. 1989. A tutorial on Hidden Markov Models and selected applications in speech
recognition, Proceedings of the IEEE, vol. 77, 256-286.
5. Samuelsson, Christer. 2000. Extending N-gram tagging to word graphs, Recent Advances in Natural
Language Processing II, ed. by Nicolas Nicolov & Ruslan Mitkov. Current Issues in Linguistic Theory (CILT),
vol. 189, pp 3-20. John Benjamins: Amsterdam/Philadelphia.
6. Shin, Jung Ho, Young S. Han & Key-Sun Choi. 1997. A HMM part-of-speech tagger for Korean with
wordphrasal relations. Recent Advances in Natural Language Processing, ed. by Nicolas Nicolov & Ruslan
Mitkov. Current Issues in Linguistic Theory (CILT) vol 136, pp 439-450. John Benjamins:
Amsterdam/Philadelphia.
209

210. Statistics Refresher
• Outcome: Individual atomic results of a (non-deterministic) experiment.
• Event: A set of results.
• Probability: Limit of target outcome over number of experiments (frequentist
view) or degree of belief (Bayesian view).
• Normalization condition: Probabilities for all outcomes sum to 1.
• Distribution: Probabilities associated with each outcome.
• Random variable: Mapping of the outcomes to real numbers.
• Joint distributions: Conducting several (possibly related) experiments and
observing the results. Joint distribution states the probability for a combination of
values of several random variables.
• Marginal: Finding the distribution of a random variable from a joint distribution.
• Conditional probability (Bayes’ rule): Knowing the value of one variable constrains
the distribution of another.
• Probability density functions: Probability that a continuous variable is in a certain
range.
• Probabilistic reasoning: Introduce evidence (set certain variables) and compute
probabilities of interest (conditioned on this evidence).
210

211. Definitions
Expectation:
Variance:
Mode:
Expectation of a function:
Properties:
211

212. Intuitions about Scale
Weight in grams if the Earth were to be a black hole.
Age of the universe in seconds.
Number of cells in the human body (100 trillion).
Number of neurons in the human brain.
Standard Blu-ray disc size, XL 4 layer (128GB).
One year in seconds.
Items in the Library of Congress (largest in the world).
Length of the Niles in meters (longest river).
212

213. Acknowledgements
• Amir Padovitz • Bran Boguraev
• Bruno Bozza • Chris Brew
• Kent Cedola • Jinho Choi
• Max Galkin • William Headden
• Manuel Reyes Gomez • Jingjing Li
• Matt Hurst • Jason Kessler
• John Langford • Mike Mozer
• Priyank Singh • Shumin Wu
• Tong Zhang
213