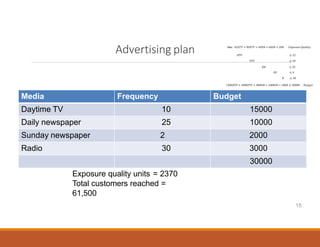
Linear programming has many applications in marketing, finance, and operations. This document discusses applications in media selection, portfolio management, and other areas. It presents an example of using linear programming to develop an optimal advertising media selection plan by maximizing exposure while staying within budget constraints. Another example optimizes investment amounts across different assets to maximize return while adhering to guidelines limiting amounts in certain industries. Solutions are provided, including dual values that provide insight into how changes in constraints would impact the optimal solutions.

1. LINEAR PROGRAMMING :
APPLICATIONS
EDITED BY: PRASAD PATIL

2. Agenda
• LPP APPLICATIONS IN MARKETING, FINANCE &
OPERATIONS

3. Introduction
Anderson, D. R., Sweeney, D. J., Williams, T. A., Camm, J. D., & Cochran, J. J. (2018). An introduction to management science: quantitative approach. Cengage learning.
3
• Linear programming has proven to be one of the most
successful quantitative approaches to decision making.
• Applications have been reported in almost every industry.
• These applications include production scheduling, media
selection, financial planning, capital budgeting,
transportation, distribution system design, product mix,
staffing, and blending.
• A mathematical model is developed for each problem
studied, and solutions are presented for most of the
applications

4. Problem definition
Anderson, D. R., Sweeney, D. J., Williams, T. A., Camm, J. D., & Cochran, J. J. (2018). An introduction to management science: quantitative approach. Cengage learning.
4
• Applications of linear programming in marketing are numerous.
• Application of LPP in Media Selection

5. Problem definition
Anderson, D. R., Sweeney, D. J., Williams, T. A., Camm, J. D., & Cochran, J. J. (2018). An introduction to management science: quantitative approach.
Cengage learning.
5
• Media selection applications of linear programming are designed to
help marketing managers allocate a fixed advertising budget to various
advertising media.
• Potential media include newspapers, magazines, radio, television, and
direct mail.
• In these applications, the objective is to maximize reach, frequency, and
quality of exposure.
• Restrictions on the allowable allocation usually arise during
consideration of company policy, contract requirements, and media
availability.
• We will llustrate how a media selection problem might be formulated and
solved using a linear programming model.

6. Problem Definition
• Relax-and-Enjoy Lake
Development Corporation is
developing a lakeside community
at a privately owned lake.
• The primary market for the
lakeside lots and homes
includes all middle- and upper-
income families within
approximately 100 miles of the
development.
• Relax-and-Enjoy employed the
advertising firm of Boone, Phillips,
and Jackson (BP&J) to design the
promotional campaign.
Anderson, D. R., Sweeney, D. J., Williams, T. A., Camm, J. D., & Cochran, J. J. (2018). An introduction to management science: quantitative approach.
Cengage learning.
6
https://images.app.goo.gl/YCSkdDcVFjven
qv49

7. Advertising Media Alternatives
7
Advertising Media No. of
Potential
Customers
Reached
Cost ($) per
Advertiseme
nt
Maximum
times
available per
Month
Exposure
Quality
Units
1. Daytime TV (1 min) 1000 1500 15 65
2. Evening TV (30 sec) 2000 3000 10 90
3. Daily newspaper (full page) 1500 400 25 40
4. Sunday newspaper magazine (1/2
page colour)
2500 1000 4 60
5. Radio, 8.00 AM or 5.00 PM news (30 sec) 300 100 30 20
Anderson, D. R., Sweeney, D. J., Williams, T. A., Camm, J. D., & Cochran, J. J. (2018). An introduction to management science: quantitative approach. Cengage learning.

8. Constraints
8
• At least 10 television commercials must be used
• At least 50,000 potential customers must be reached
• No more than $18,000 may be spent on television
advertisements
• What advertising media selection plan should be
recommended?

9. Decision Variables
9
• DTV = number of times daytime TV is used
• ETV = number of times evening TV is used
• DN = number of times daily newspaper is
used
• SN = number of times Sunday newspaper is
used
• R = number of times radio is used

10. Problem formulation
Anderson, D. R., Sweeney, D. J., Williams, T. A., Camm, J. D., & Cochran, J. J. (2018). An introduction to management science: quantitative approach. Cengage learning.
10

11. Constraints
11

13. Reduced cost and Dual Value
• The Reduced Costs column in Figure indicates
that the number of exposure quality units for
evening TV would have to increase by at least 65
before this media alternative could appear in the
optimal solution.
• Note that the budget constraint has a dual
value of 0.06.
• Therefore, a $1.00 increase in the advertising
budget will lead to an increase of 0.06 exposure
quality units.
• The dual value of –25.000 for constraint 7 indicates
that increasing the required number of television
commercials by 1 will decrease the exposure
quality of the advertising plan by 25 units
13

14. Dual Value
14
• Alternatively, decreasing the required number of television
commercials by 1 will increase the exposure quality of the
advertising plan by 25 units.
• Thus, Relax-and-Enjoy should consider reducing the requirement of
having at least 10 television commercials.

15. Advertising plan
Media Frequency Budget
Daytime TV 10 15000
Daily newspaper 25 10000
Sunday newspaper 2 2000
Radio 30 3000
30000
Exposure quality units = 2370
Total customers reached =
61,500
15

16. Portfolio Selection
16
• Portfolio selection problems involve situations in which a financial manager
must select specific investments—for example, stocks and bonds—from a
variety of investment alternatives.
• Managers of mutual funds, credit unions, insurance companies, and banks
frequently encounter this type of problem.
• The objective function for portfolio selection problems usually is
maximization of expected return or minimization of risk.
• The constraints usually take the form of restrictions on the type of
permissible investments, state laws, company policy, maximum permissible
risk, and so on.
Anderson, D. R., Sweeney, D. J., Williams, T. A., Camm, J. D., & Cochran, J. J. (2018). An introduction to management science: quantitative approach.
Cengage learning.

17. Problem
17
• Consider the case of a Mutual Funds company just obtained $100,000 by
converting industrial bonds to cash and is now looking for other
investment opportunities for these funds.
• The firm’s top financial analyst recommends that all new investments be
made in the oil industry, steel industry, or in government bonds.
• Specifically, the analyst identified five investment opportunities and
projected their annual rates of return
Anderson, D. R., Sweeney, D. J., Williams, T. A., Camm, J. D., & Cochran, J. J. (2018). An introduction to management science: quantitative approach.
Cengage learning.

18. Investment
opportunities
18
Investment Projected Rate of Return %
Atlantic Oil 7.3
Pacific Oil 10.3
Midwest steel 6.4
Huber Steel 7.5
Government Bonds 4.5
Anderson, D. R., Sweeney, D. J., Williams, T. A., Camm, J. D., & Cochran, J. J. (2018). An introduction to management science: quantitative approach.
Cengage learning.

19. Investment guidelines.
19
• Neither industry (oil or steel) should receive more than $50,000.
• Government bonds should be at least 25% of the steel industry
investments.
• The investment in Pacific Oil, the high-return but high-risk investment,
cannot be more than 60% of the total oil industry investment.
Anderson, D. R., Sweeney, D. J., Williams, T. A., Camm, J. D., & Cochran, J. J. (2018). An introduction to management science: quantitative approach.
Cengage learning.

20. Problem
20
• What portfolio recommendations—investments and amounts—should be
made for the available $100,000?
Anderson, D. R., Sweeney, D. J., Williams, T. A., Camm, J. D., & Cochran, J. J. (2018). An introduction to management science: quantitative approach.
Cengage learning.

21. Formulation
21
• A = dollars invested in Atlantic Oil
• P = dollars invested in Pacific Oil
• M = dollars invested in Midwest Steel
• H = dollars invested in Huber Steel
• G = dollars invested in government bonds
Anderson, D. R., Sweeney, D. J., Williams, T. A., Camm, J. D., & Cochran, J. J. (2018). An introduction to management science: quantitative approach.
Cengage learning.

22. Objective function for maximizing the total return
•
Anderson, D. R., Sweeney, D. J., Williams, T. A., Camm, J. D., & Cochran, J. J. (2018). An introduction to management science: quantitative approach.
Cengage learning.
22

23. Investment available
23
A + P + M + H + G = 100,000
Anderson, D. R., Sweeney, D. J., Williams, T. A., Camm, J. D., & Cochran, J. J. (2018). An introduction to management science: quantitative approach.
Cengage learning.

24. Neither the oil nor the steel industry should receive more than $50,000
Anderson, D. R., Sweeney, D. J., Williams, T. A., Camm, J. D., & Cochran, J. J. (2018). An introduction to management science: quantitative approach.
Cengage learning.
24

25. Government bonds be at least 25% of the steel
industry investment
25
G ≥ 0.25(M+H)
Anderson, D. R., Sweeney, D. J., Williams, T. A., Camm, J. D., & Cochran, J. J. (2018). An introduction to management science: quantitative approach.
Cengage learning.

26. Pacific Oil cannot be more than 60% of the total oil industry investment
Anderson, D. R., Sweeney, D. J., Williams, T. A., Camm, J. D., & Cochran, J. J. (2018). An introduction to management science: quantitative approach.
Cengage learning.
26

27. Complete linear programming model
•
27
Anderson, D. R., Sweeney, D. J., Williams, T. A., Camm, J. D., & Cochran, J. J. (2018). An introduction to
management science: quantitative approach. Cengage learning.

29. Solution for portfolio
management problem
Anderson, D. R., Sweeney, D. J., Williams, T. A., Camm, J. D., & Cochran, J. J. (2018). An introduction to management science: quantitative approach.
Cengage learning.
29

30. Solution for portfolio management problem
30
• Note that the optimal solution indicates that the portfolio should be
diversified among all the investment opportunities except Midwest Steel.
• The projected annual return for this portfolio is $8000, which is an overall
return of 8%.
Anderson, D. R., Sweeney, D. J., Williams, T. A., Camm, J. D., & Cochran, J. J. (2018). An introduction to management science: quantitative approach.
Cengage learning.

31. Solution for portfolio management problem : Dual value
31
• The dual value for the available funds constraint provides information on
the rate of return from additional investment funds.
Anderson, D. R., Sweeney, D. J., Williams, T. A., Camm, J. D., & Cochran, J. J. (2018). An introduction to management science: quantitative approach.
Cengage learning.

32. Solution for portfolio management problem : Dual Value
• The optimal solution shows the dual value for the
Steel Industry constraint is zero.
• The reason is that the steel industry maximum isn’t a
binding constraint; increases in the steel industry limit
of $50,000 will not improve the value of the optimal
solution.
• Indeed, the slack variable for this constraint shows
that the current steel industry investment is $10,000
below its limit of $50,000.
• The dual values for the other constraints are nonzero,
indicating that these constraints are binding.
Anderson, D. R., Sweeney, D. J., Williams, T. A., Camm, J. D., & Cochran, J. J. (2018). An introduction to management science: quantitative approach.
Cengage learning.
32

33. Solution for portfolio management problem : dual Value
• The dual value of 0.069 for Funds Available
shows that the value of the optimal solution
can be increased by 0.069 if one more dollar
can be made available for the portfolio
investment.
• If more funds can be obtained at a cost of less
than 6.9%, management should consider
obtaining them.
• However, if a return in excess of 6.9% can be
obtained by investing funds elsewhere (other
than in these five securities), management
should question the wisdom of investing the
entire $100,000 in this portfolio.
Anderson, D. R., Sweeney, D. J., Williams, T. A., Camm, J. D., & Cochran, J. J. (2018). An introduction to management science: quantitative approach.
Cengage learning.
33

34. Portfolio management problem : dual value
• Note that the dual value for
constraint 4 is negative at –0.024.
• This result indicates that increasing
the value on the right-hand side of
the constraint by one unit can be
expected to decrease the objective
function value of the optimal
solution by 0.024.
Anderson, D. R., Sweeney, D. J., Williams, T. A., Camm, J. D., & Cochran, J. J. (2018). An introduction to management science: quantitative approach.
Cengage learning.
34